Il principio di relatività
Come gli altri principi fisici, anche il principio di relatività è rispettato dalla natura senza eccezioni, e tale situazione basta a legittimarlo, anche se non basta a chiarire la natura del principio stesso. Il principio di relatività è stato scoperto e sostenuto da un solo scienziato, Einstein, e forse non è mai stato enunciato in una forma ufficiale.
Useremo i termini "osservatore", "riferimento" e "sistema di coordinate" come equivalenti fra loro. Il principio in sostanza afferma che "le stesse leggi fisiche sono valide per tutti gli osservatori" e pertanto "le leggi devono avere una forma che sia capace di adattarsi al riferimento". Si intende, inoltre, che "deve esistere una trasformazione che collega le coordinate che un medesimo evento possiede nei diversi riferimenti".
In mancanza di quest'ultimo requisito, si avrebbe una sconclusionata frantumazione della realtà e non una teoria fisica coerente.
Il principio di relatività quindi deve valere anche per osservatori in moto e per osservatori assoggettati all'influenza della gravità, problema che la teoria della relatività ristretta risolve soltanto in parte.
Fra gli altri principi fisici, il principio di relatività presenta un carattere di maggiore astrazione: esso è una specie di super-legge, che condiziona le altre leggi fisiche. Queste, dovendo adattarsi al riferimento, risulteranno prevalentemente espresse tramite forme invarianti e concetti di geometria superiore.
Il principio di relatività presenta importanza pratica a causa delle deduzioni, che ne furono tratte per opera del suo stesso scopritore.
Meccanica classica e principio di relatività
Il principio di relatività fu riconosciuto da Galileo, il quale fece l'esempio di una grande nave che avanza in mare tranquillo, dove i passeggeri sotto coperta osservano che tutti i fenomeni avvengono come se fossero sulla terra ferma. Poiché Galileo asseriva che la Terra si muove attorno al Sole, lo stesso principio gli consentiva altresì di spiegare come mai essa “sembra ferma”. Scriviamo con le nostre consuete notazioni la trasformazione di Galileo, valida fra due osservatori dotati di velocità relativa v lungo l'asse x (uno degli osservatori è contraddistinto mediante un apice '):



Ad ambedue le colonne può aggiungersi:
t = t'
In piena conformità con il principio di relatività, i due osservatori sono equivalenti, possono osservare i medesimi eventi, possono misurarne le coordinate, e mediante la trasformazione di Galileo possono dedurre le misure prese da un osservatore da quelle di un altro. La legge fondamentale della meccanica classica (forza = massa x accelerazione) è valida nella sostanza e nella forma per ambedue gli osservatori. Difatti, le derivate prime (rispetto a t) della prima e della seconda colonna della trasformazione differiscono per la costante v, e le derivate seconde sono identiche. Poiché nella legge figurano solo le derivate seconde (indicate dalla accelerazione), la legge è invariante rispetto alla trasformazione di Galileo. Queste considerazioni sono valide per gli osservatori inerziali, cioè dotati di moto rettilineo uniforme (un osservatore rotante non è inerziale, ma nell’esempio della Terra possiamo trascurare la differenza). Per concludere, in meccanica classica tutti gli osservatori inerziali sono equivalenti, e nessuna esperienza è in grado di decidere se uno di essi sia privilegiato ovvero "fisso".
Elettrodinamica classica e principio di relatività
Fra osservatori inerziali, le leggi della elettrodinamica classica non sono invarianti nella forma. Difatti esse contengono una derivata prima, che è la velocità, nella legge di Lorentz. Da ciò non deriva nessuna sostanziale divergenza fra le previsioni operate dai diversi osservatori, ma solo una differenza formale (quello che a un osservatore fisso rispetto al campo magnetico appare come forza di Lorentz, ad un osservatore fisso rispetto alla carica appare come campo elettrico), che peraltro sarebbe superabile mediante il concetto di "trasformazione di campo". Tale differenza però strideva di fronte alle convinzioni di Einstein, e lo condusse ad un geniale superamento.
Tutto ciò è vero nel campo delle velocità ordinarie della elettrodinamica. Le stesse leggi della elettrodinamica peraltro, rielaborate da Maxwell, mostrano la possibilità che una perturbazione dei campi si propaghi con velocità molto maggiore: la velocità C della luce. Nel fenomeno della propagazione luminosa, il principio di relatività cozza contro le leggi classiche in modo molto più sostanziale e traumatico. Difatti la velocità di un fronte luminoso è la stessa per tutti gli osservatori; questo fatto va d'accordo con le leggi della elettrodinamica classica, va d'accordo con la prima parte del principio di relatività, va d'accordo con tutti i fatti sperimentalmente osservati, però non si capisce più quale sia la trasformazione di coordinate da applicare. Se applichiamo la trasformazione di Galileo, suggerita dal senso comune, risulta che il fronte non può avere la stessa velocità rispetto a due osservatori, che a loro volta si muovono. Come dire che il vento non può avere la stessa velocità rispetto alla pista e rispetto all'aereo. E' come se il fronte avesse la capacità di sdoppiarsi per i due osservatori, in contrasto con la seconda parte del principio di relatività.
Questo contrasto non può risolversi nel riferimento tridimensionale fin qui adottato, bensì in un nuovo tipo di riferimento, di cui si dirà nel paragrafo seguente.
Lo spazio-tempo
L'insieme costituito da un punto e da un istante viene chiamato evento e può ancora rappresentarsi come un oggetto in un riferimento a quattro dimensioni. Bisogna però chiarire che l'istante deve essere misurato in prossimità del punto, cioè il tempo è un fatto locale.
Pertanto, ogni sistema di riferimento è costituito dai soliti 3 assi coordinati x,y,z e da infiniti orologi dislocati uno in ciascun punto. Detti orologi non sono indipendenti, bensì sincroni, nel senso che la velocità di un fronte luminoso, intesa come derivata dello spazio rispetto al tempo locale, deve risultare costante in qualsiasi direzione di propagazione e pari a C.
Si possono ideare semplici procedure, per verificare se due orologi siano sincroni; queste procedure non differiscono da ciò che ognuno di noi farebbe, se dovesse regolare esattamente il proprio orologio su quello di un amico situato oltre oceano, mentre ha la possibilità di conversare con lui via radio (ammesso di potere apprezzare intervalli di pochi centesimi di secondo).
In un dato riferimento spazio-temporale, come "istante" possiamo intendere l'insieme degli infiniti orologi che segnano lo stesso tempo, come "punto" possiamo intendere un orologio fisso, e la contemporaneità quasi svanisce perchè ha senso soltanto per eventi vicini fra loro o per un singolo osservatore inerziale.
Nei problemi unidimensionali, in cui il moto avviene solamente lungo l'asse x, lo spazio-tempo presenta solamente gli assi x,t e può essere agevolmente rappresentato sul foglio (diagrammi di Minkowski).
Lo spazio-tempo è la rappresentazione (immobile) dello spazio e dei movimenti che vi si svolgono. Quando si parla di "cambiamento di coordinate" nello spazio-tempo ci si riferisce al passaggio da un osservatore a un altro, che sia non soltanto diversamente orientato, ma anche in movimento rispetto al primo. Il cambiamento di coordinate puramente spaziale resta relegato al ruolo di un caso particolare, che interessa soltanto la sezione spaziale dello spazio-tempo.
Due riferimenti spazio-temporali possono avere la stessa origine, nel senso che le origini dei due riferimenti spaziali si toccano mentre ambedue gli orologi posti nelle origini segnano il tempo zero. Non è agevole pensare in termini spazio-temporali quindi consideriamo separatamente le sezioni temporale e spaziale dello spazio-tempo.
Nella teoria della relatività ristretta ci si occupa soltanto di osservatori inerziali.
Si può dimostrare che, nel piano di Minkowski, i riferimenti inerziali aventi la stessa origine formano una stella di riferimenti cartesiani ad assi obliqui, tutti simmetrici rispetto alle stesse diagonali. Risulta pertanto immediato leggere le coordinate spaziale e temporale che un medesimo evento possiede nei diversi riferimenti. Nessuno di essi è privilegiato, benchè soltanto quello, usato per iniziare il ragionamento, possieda assi ortogonali.
Nei casi unidimensionali, che sono quelli propriamente trattati dalla Relatività ristretta, il piano di Minkowski è "lo" spazio-tempo nel senso che è la sede in cui gli eventi sono riscontrabili come fatti oggettivi.
L’invariante
Ricordiamo che le componenti x,y,z di un segmento non hanno carattere oggettivo poichè dipendono dall'orientamento del riferimento rispetto al segmento. Viceversa, la lunghezza l del segmento è oggettiva e non dipende da detto orientamento. La lunghezza peraltro può esprimersi in funzione delle componenti:

Al variare del riferimento, variano separatamente x,y,z ma sempre in modo che la l risultante rimanga invariata.
Analogamente, nello spazio-tempo, le misure, o componenti, spaziale e temporale di un segmento (definito da due eventi che fungono da estremi) non sono indipendenti dal riferimento. Risulta invece invariante la seguente espressione:

dove C è una costante pari alla velocità della luce.
L'invariante s ha il significato geometrico di una "lunghezza lineare" nello spazio-tempo. Esso risulta omogeneo con t, ma può anche essere definito in modo diverso, omettendo il fattore C2 a primo membro e/o premettendovi un segno meno (questa varietà di definizioni potrebbe far pensare che s non sia una vera e propria grandezza fisica).
Notiamo che la propagazione della luce è rappresentata da segmenti aventi s=0, in qualsiasi riferimento.
E' valida anche la seguente espressione differenziale :

che si può applicare a ciascun elemento di una linea curva.
La funzione s delle coordinate, che gode di alcune proprietà caratteristiche delle lunghezze, prende il nome di metrica. Vedremo più avanti (relatività generale) che in alcuni casi la metrica deve variare nella forma, mai nel valore.
Primi paradossi
Il fattore C assume il ruolo di "tasso di conversione" fra spazio e tempo, dato che ambedue contribuiscono, con segni discordi, a determinare la lunghezza s nello spazio-tempo. Quando un punto P si muove, descrivendo una traiettoria nello spazio (anzi, dovremmo dire in "uno" spazio, dato che ogni osservatore ha il proprio), la rappresentazione oggettiva nello spazio-tempo è data da una successione di eventi contigui, che prende il nome di "linea di universo". Ripetiamo che la misura di una linea di universo (cioè l'integrale dei ds elementari lungo tale linea) è oggettiva ed invariante per tutti gli osservatori, mentre la lunghezza della traiettoria spaziale e la durata del moto possono apparire diverse a diversi osservatori. Notiamo che nei casi reali, di movimenti più lenti della luce, il ds2 risulta positivo ed il ds risulta reale; ciò dipende dalla definizione adottata. Consideriamo il particolare osservatore che sia solidale col punto materiale in moto. A quest'osservatore il punto appare immobile nell'origine (x=y=z=0) mentre il tempo fluisce normalmente. Il tempo locale, nell'origine spaziale di un cosiffatto osservatore, dove si trova il punto materiale P, prende il nome di "tempo proprio della particella P" e non è altro che il tempo segnato da un orologio in moto assieme a P. Il tempo segnato da un orologio, in moto inerziale, é la misura della sua linea di universo s. Difatti nella (1), posto x=y=z=0, i contributi spaziali sono nulli e resta solo il contributo temporale. Se tale orologio viene a sua volta osservato da un altro osservatore ("fisso"), quest'ultimo gli attribuirà una certa traiettoria, diversa da zero. Però la misura della linea di universo non può cambiare, e pertanto, essendo i contributi spaziale e temporale di segno discorde, per riottenere lo stesso risultato, avendo dato un valore positivo allo spazio percorso, bisogna maggiorare anche la stima del tempo. Dunque il primo osservatore (orologio in moto) dirà: io sono fermo ed è passato un tempo tp. Il secondo osservatore ("fisso") dirà al primo: tu ti sei spostato di una lunghezza l ed è passato un tempo tl tale che

Il tempo proprio tp segnato dall'orologio in moto sarà minore del tempo locale tl segnato dagli orologi "fissi", che il primo incontra sul proprio cammino, a man mano che aumenta lo spazio l percorso. Quando un orologio (ideale) va in ritardo rispetto ad un altro orologio ideale, posto nello stesso punto, possiamo concludere che l'orologio che ritarda, dopo che è stato sincronizzato, ha percorso un certo spazio. Gli orologi in moto ritardano, cioè misurano la propria linea di universo, che è una combinazione (1) fra il tempo locale e lo spazio percorso, con segni discordi. Un paradosso nasce nel momento in cui due orologi vicini, dopo essersi sincronizzati e poi mossi, tornassero a incontrarsi un'altra volta. A questo punto, quale dei due dovrebbe andare indietro rispetto all'altro? Sembra quasi che un simile esperimento possa confutare lo stesso principio di relatività, identificando uno dei due orologi come privilegiato, ovvero fisso in assoluto. Qui ci limitiamo ad osservare che la metrica (1) è valida solo per osservatori inerziali, i quali non possono incontrarsi due volte; peraltro alcuni esperimenti un po' maccheronici, condotti considerando come "fisso" un orologio al suolo, e come "mobile" un orologio imbarcato su un aereo in circumnavigazione, hanno evidenziato un rallentamento dell'orologio mobile, che dopo il viaggio andava un po' indietro rispetto all'altro. (Per l'esattezza, dobbiamo aggiungere che nella valutazione quantitativa di questo esperimento, condotto con due aerei, si è dovuto tenere conto della rotazione terrestre e del campo gravitazionale).
La trasformazione di Lorentz
Una trasformazione di coordinate che si rispetti, non deve far variare l'invariante (da questo punto di vista, un semplice cambiamento di scala sarebbe una trasformazione poco rispettabile, però si può ovviare all'inconveniente introducendo un fattore di normalizzazione). Nello spazio, l'invariante è la lunghezza dL di un segmento elementare. Né la trasformazione di Galileo fra osservatori inerziali, né una rotazione di assi, né un passaggio in coordinate polari fanno variare tale lunghezza, anzi le formule di trasformazione talvolta si ottengono proprio imponendo la condizione di invarianza. Analogamente, nello spazio-tempo, vi è una trasformazione che rispetta la invarianza del ds fra osservatori inerziali.
Questa è la trasformazione di Lorentz:
posto:
scriviamo:




essendo v la velocità fra il sistema x,y,z,t e il sistema x',y',z',t' (si assumano gli assi x,x' nella stessa direzione di v, e gli assi corrispondenti paralleli). Lo spazio-tempo non possiede un riferimento privilegiato; ogni osservatore inerziale usa le proprie coordinate, e fra tutte queste vale la trasformazione di Lorentz, la quale pertanto ha un ruolo essenziale nel definire lo spazio-tempo stesso.
La contrazione delle lunghezze
In un dato riferimento, la lunghezza di un segmento materiale AB è data da:

Se il segmento è in moto rispetto al riferimento, si intende che le x,y,z vanno misurate tutte con lo stesso valore della coordinata t (tempo locale). L'estremo A deve passare dalla posizione di coordinate xA,yA,zA mentre l'orologio fisso posto in A segna un tempo tA eguale al tempo tB segnato dall'orologio fisso (sincrono col precedente) posto nella posizione di coordinate xB,yB,zB nell'istante in cui l'estremo B passa in quella posizione.
Supponiamo che l'estremo A passi per l'origine al tempo zero e riduciamo il problema al caso unidimensionale lungo l'asse x. La lunghezza del segmento sarà:
L = xB (coordinata rilevata nell'istante in cui tB = 0) nel riferimento "fisso"
L' = x'B (coordinata rilevata con t'B qualsiasi) nel riferimento proprio del segmento in moto.
Dalla prima riga della trasformazione di Lorentz, con tB=0 si ottiene x'B=kxB cioè
L = L'/k (contrazione di Lorentz)
Notiamo che il passaggio dell'estremo B nell'istante tB=0 nella posizione xB=L avviene mentre l'orologio sincrono, solidale con l'estremo B, segna un tempo t'B diverso da zero, che può calcolarsi dall'ultima riga della trasformazione di Lorentz:
t'B=-kvxB/C2=-L'v/C2.
Ricapitolando: la lunghezza di un segmento spaziale nello spazio-tempo viene definita in un modo più complicato di quello a cui siamo abituati, perché bisogna accertarsi che le posizioni dei due estremi vengano rilevate con lo stesso tempo locale, cioè la misura di una lunghezza coinvolge anche delle misure di tempo locale. Peraltro la conclusione a cui siamo giunti è di validità generale: non soltanto i segmenti, ma anche i vettori elettrici e magnetici subiscono la contrazione di Lorentz. La contrazione è reciproca fra due osservatori in movimento.
Vorrei anche dire che la definizione del tempo locale e le sue conseguenze non sono soltanto una complicazione rispetto al concetto di tempo assoluto, ma anche un discorso più logico e più preciso. Lo spazio-tempo poteva essere scoperto dai filosofi ancora prima che le onde elettromagnetiche ne svelassero la necessità in termini quantitativi.
La trasformazione di Lorentz comporta anche la "dilatazione del tempo", ma di questa ci eravamo già occupati parlando dei primi paradossi e deducendola direttamente dall'invariante s. Dilatazione del tempo e contrazione dello spazio non sono effetti apparenti bensì reali, nello spazio-tempo, che è l'unica sede in cui diversi osservatori in moto possono coesistere coerentemente.
Non ha molto senso “fotografare” nello spazio-tempo un corpo esteso in moto. Poichè il tempo locale dipende dal riferimento, quale data scriveremmo sulla fotografia? Prendiamo il più semplice corpo in moto: un segmento spaziale. Possiamo rappresentarne gli estremi, mediante due separate linee spazio-temporali. Ma la "graduazione" del tempo locale lungo tali linee dipende dall'osservatore, dunque per ogni posizione di un estremo non si può oggettivamente indicare dove si trovi l'altro estremo lungo la propria linea. Nello spazio-tempo non esistono propriamente immagini rigide di oggetti estesi, ma archivi di coordinate di eventi variamente collegati. Non troppo rassicurante.
Costruzione del diagramma di Minkowski
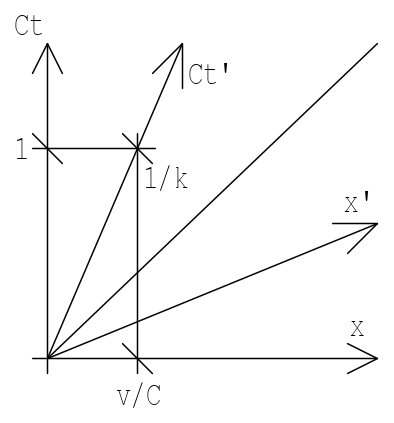
Partiamo dal riferimento "fisso" cartesiano in assi ortogonali, x orizzontale per le ascisse e Ct verticale per le ordinate. Un punto geometrico o un orologio fisso viene rappresentato da una retta verticale. Un "istante" è rappresentato da una retta orizzontale cioè consiste nell'insieme degli orologi che segnano lo stesso tempo locale in un dato riferimento. Un segmento geometrico rigido, cioè una coppia di punti aventi distanza costante, è rappresentato da due rette parallele. La diagonale bisettrice degli assi, segnata nella figura, rappresenta un punto che si allontana dall'origine con la velocità della luce. I movimenti più lenti della luce vengono rappresentati da linee aventi pendenza maggiore della detta diagonale.
In particolare, la semiretta Ct' rappresenta un punto che si allontana dall'origine con velocità v.
Si dimostra che la coppia di assi x', Ct' simmetrici rispetto alla detta bisettrice, rappresenta anche un riferimento cartesiano in assi obliqui e precisamente quel riferimento che si allontana dall'origine con velocità v. Nella figura è mostrata anche la graduazione da riportare sui detti assi obliqui, facendo uso del fattore k di cui si è detto a proposito della trasformazione di Lorentz (2). Abbiamo sullo stesso piano diversi assi cartesiani con graduazioni non sovrapponibili, è chiaro che si tratta di una situazione metrica del tutto particolare.
Ogni punto del piano di Minkowski rappresenta un evento oggettivo, e ogni linea rappresenta un punto geometrico oggettivo, le cui coordinate possono leggersi sia sugli assi x, Ct per quanto riguarda il riferimento "fisso", sia sugli assi x', Ct' per quanto riguarda il riferimento "mobile".
Il luogo degli eventi in cui s=0, in tutti i riferimenti citati, è la bisettrice degli assi.
I luoghi in cui s=costante, correggetemi se sbaglio, sono iperboli che si appoggiano alle bisettrici come asintoti.
Un po' di meccanica relativistica
Consideriamo il moto di un sistema isolato P composto da una particella o da una somma di particelle. In meccanica classica, il tempo t è invariante, e la velocità v è la derivata dello spazio rispetto a t. Nello spazio tempo, il tempo proprio s della particella è invariante, e la quadrivelocità u è un vettore a 4 componenti (quadrivettore) che sono le derivate delle 4 componenti spazio-temporali Ct,x,y,z rispetto a s. Il tempo t perde il proprio ruolo assoluto ed assume il significato di tempo locale, di cui abbiamo già parlato. La prima componente della quadrivelocità (derivata del tempo locale t rispetto al tempo proprio s, moltiplicata per la costante C) vale k. Questo risultato si può ottenere dall'ultima riga della trasformazione di Lorentz ponendo x'=0, t'=s, cioè identificando il sistema P con l'origine del secondo riferimento. Notiamo che la velocità v=dx/dt non è del tutto eliminata, ma rimane nella definizione di k. La cosa stupefacente della relatività è che tutti i principi fisici già assodati nella fisica classica, valgono formalmente anche nello spazio tempo, mentre la loro interpretazione fisica può addirittura consentire delle conclusioni profondamente innovative, come vedremo fra poco a proposito della celebre equivalenza massa-energia. Il quadrimpulso è il prodotto della quadrivelocità per la massa m. Il principio di conservazione dell'impulso (o prima legge di Newton), dice che esso è costante, cioè le sue componenti sono costanti. La prima componente, moltiplicata per la costante C2, diventa
kmC2=cost ovvero mdC2=cost ponendo km=md.
Il prodotto mdC2 ha le dimensioni di una energia (energia totale) ed md si chiama "massa dinamica" mentre m è la massa statica. Questa prima componente del principio di conservazione dell'impulso assume, nella meccanica relativistica, il ruolo che nella meccanica classica ha il principio di conservazione dell'energia. La massa dinamica non è una caratteristica oggettiva e invariante della particella, perché dipende anche dalla velocità v e quindi dall'osservatore. Torniamo a usare la massa m, propria della particella, per ottenere una legge di conservazione dotata di significato fisico. Inoltre cerchiamo di sfruttare il fatto che k è pari ad 1, quando v=0 cioè il sistema è a riposo.
kmC2 = mC2(1+(k-1)) = mC2+(k-1)mC2 = mC2+Ek = cost
ponendo (k-1)mC2=Ek (energia cinetica relativistica).
In sostanza abbiamo spezzato l'energia totale in due termini: un contributo cinetico Ek , ed uno "di riposo" mC2 di cui la meccanica classica non riconosceva la presenza mentre quì è largamente prevalente. Per una particella con v<<C, mediante uno sviluppo in serie si ottiene Ek=(circa)mv2/2 cioè l'energia cinetica relativistica coincide con quella classica. Pertanto in meccanica relativistica, nei sistemi isolati, si conserva la somma della massa m (moltiplicata per la costante C2) con l'energia cinetica Ek, mentre la sola massa e la sola energia separatamente non si conservano. Sono leciti processi, o anche semplicemente fatti dinamici (urti) in cui avvengono trasformazioni di massa in energia cinetica o viceversa, dove C2 funge da tasso di scambio. Poiché a sua volta l'energia cinetica può trasformarsi in ogni altra forma di energia, possiamo dire che la massa statica m (la quale è invariante da un osservatore all'altro) è una manifestazione di tutte le forme di energia (cioè capacità di compiere lavoro) possedute dal corpo eccettuata la energia cinetica, mentre la massa dinamica md (la quale si conserva nei sistemi isolati) include anche la energia cinetica. Poiché la energia cinetica non ha carattere oggettivo ma dipende dalla velocità che l'osservatore attribuisce al corpo (cioè è una energia fatta di spazio e di tempo, legata al sistema di riferimento), la teoria della relatività, che è tutta imperniata sul ruolo del sistema di riferimento, riserva una posizione un po' particolare alla energia cinetica rispetto a tutte le altre forme di energia. Per esempio, l'energia termica, pure essendo (da un punto di vista microscopico) energia cinetica, risulta oggettivamente distinguibile dalla energia cinetica di assieme posseduta da un corpo in funzione della velocità che un osservatore gli attribuisce, e pertanto la energia termica contribuisce alla massa statica, non alla Ek. La legge di inerzia si può formulare dicendo che la linea di universo del baricentro di un sistema, su cui non agiscano forze esterne, è una geodetica (linea di minima lunghezza) dello spazio-tempo. Per quanto riguarda la seconda legge di Newton, nella forma f=d(md v)/dt, anch'essa è valida nello spazio tempo, però sorge la necessità di definire la forza f. Con opportune convenzioni, nella sezione spaziale dello spazio tempo, nei fenomeni puramente elettrodinamici (non considerando l'energia radiante) risulta valida l'espressione della forza elettrica di Coulomb e anche quella di Lorentz. Vale la definizione di lavoro (prodotto scalare forza x spostamento) ed esso risulta pari alla variazione di Ek. Come velocità ed accelerazione, nella sezione spaziale, bisogna tornare ad intendere le derivate rispetto al tempo locale, e l'impulso è il prodotto della velocità per la massa dinamica md. Può considerarsi un triangolo energetico, in cui un cateto è l'energia di riposo mC2, l'altro cateto è l'impulso moltiplicato per C, e l'ipotenusa risulta pari alla energia totale E. Questo tipo di elettrodinamica può adattarsi allo studio delle macchine acceleratrici di particelle. Riassumendo, la massa di un corpo ne rappresenta l'inerzia ed è pari alla somma delle energie che esso ha ricevuto.
Passato, presente e futuro nello spazio-tempo
Grazie alla trasformazione di Lorentz, se un fenomeno A (secondo un osservatore) avviene prima di una altro fenomeno B (cioè tA < tB) , può darsi che ci siano altri osservatori per i quali il fenomeno A invece avviene successivamente a B (cioè t'A > t'B). Questa situazione sembrerebbe che possa vanificare il secondo principio della termodinamica, il quale asserisce che l'entropia di un sistema isolato cresce nel tempo, e dunque presuppone una oggettiva distinzione fra passato e futuro. Una analisi più attenta consente di definire passato, presente e futuro nello spazio-tempo in accordo con le esigenze della termodinamica e della causalità. Diciamo subito che, fra eventi spazialmente vicini, la situazione è quella classica e cioè:
A appartiene al passato di B se tA < tB
A appartiene al presente di B se tA = tB
A appartiene al futuro di B se tA > tB
Fra eventi comunque distanti, invece, chiamando dAB la distanza spaziale fra A e B
A appartiene al passato di B se tB - tA > dAB/C
A appartiene al presente di B se tA = tB ; dAB=0.
A appartiene al futuro di B se tA - tB > dAB/C
A appartiene all'altrove di B negli altri casi
Un evento può essere causato da un altro evento solo se appartiene al suo futuro, altrimenti gli eventi sono causalmente indipendenti fra loro. Difatti, qualsiasi interazione fra eventi non può correre più veloce di C (velocità della luce). Il futuro di un evento nello spazio-tempo è delimitato da una ipersuperficie conica col vertice sull'evento, che rappresenta un lampo di luce che si propaga a partire dall'evento stesso. Non tutte le linee di universo rappresentano il moto di un punto materiale, ma solo quelle che si mantengono sempre all'interno dei propri coni. I principi di conservazione della fisica (per esempio, la conservazione della carica) valgono in modo istantaneo; la relatività dimostra che essi debbono valere non solo in modo istantaneo, ma anche in modo locale.
La velocità della luce
Nello spazio-tempo, la luce è stata utilizzata come segnale per stabilire la sincronizzazione fra orologi distanti. La trasformazione di Lorentz può dedursi in base all'ipotesi che la velocità della luce sia invariante fra osservatori inerziali. Se fosse possibile superare la velocità della luce, sarebbe anche possibile riuscire a ottenere informazioni dal futuro. Per accelerare una particella fino alla velocità della luce, occorre somministrarle una quantità infinita di energia. Da tutto ciò si ha la conferma che la velocità della luce C nel vuoto è costante ed è insuperabile da parte degli altri corpi (incluso qualsiasi tipo di vettore di informazioni). Naturalmente, esistono mezzi nei quali la velocità della luce è alquanto inferiore; aggiungo che, guardando una notte stellata, lo sguardo può spostarsi più velocemente della luce, ma non determina alcuna interazione fra gli oggetti osservati. La velocità di cui parliamo é la classica derivata dello spazio rispetto al tempo t, e non va confusa con la quadrivelocità, che è derivata rispetto al tempo proprio s, e può raggiungere qualsiasi valore (la componente temporale è pari a k e vale infinito nel caso dei fotoni, mentre vale uno nel caso di oggetti fermi rispetto al riferimento). Da parte di alcuni, la costanza della velocità della luce viene addirittura confusa con lo stesso principio di relatività. Ho preferito enunciare il principio di relatività in una forma che sia la più simile alla concezione di Einstein, e poi trattare la velocità della luce come un fatto sperimentale compatibile con quel principio. Lo spazio-tempo e la sua metrica costituiscono l'unico mezzo, fino ad oggi, per fornire una descrizione razionale dei fatti osservati. Tutti i tentativi basati sulla fisica "fluodinamica" dell'etere sono falliti, o non sono arrivati allo stesso sviluppo. Oggi la fisica relativistica è consolidata e anche perfezionata rispetto alla trattazione alquanto euristica di Einstein, ma in alcuni rimane il dubbio se lo spazio-tempo e la sua metrica siano artificio o realtà. Ma quand'anche fosse un artificio, in grado di spiegare tante cose reali, verrebbe a proposito il verso di Dante (sulla crescita del Cristianesimo): "questo è miracol che gli altri sopravanza".

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)