"Una carica
 è disposta uniformemente sul volume di una sfera di raggio
è disposta uniformemente sul volume di una sfera di raggio  dentro cui si trovano due cavità sferiche simmetriche rispetto al centro, di raggio
dentro cui si trovano due cavità sferiche simmetriche rispetto al centro, di raggio  .
.Determinare il campo elettrico in tutti i punti di una retta passante per il centro della sfera e delle due cavità, disegnandone il grafico."
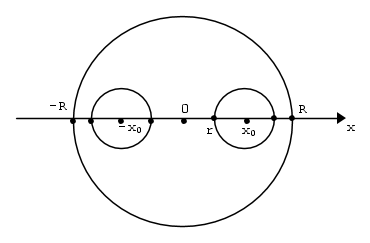
Ho disposto il centro della sfera di raggio R nel punto O=(0,0) e i centri delle due sfere di raggio r sull'asse x.
Ho calcolato E(x) con la sovrapposizione degli effetti e mi risulta:









Situazione simmetrica per x < 0.
Dal momento che questo è uno degli 8 punti del compito d'esame, non c'è molto tempo per disegnare il grafico, e quindi vorrei sapere come si può procedere a disegnare il grafico a occhio con questi dati a disposizione perché non mi è venuto nulla in mente.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)
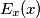 .
.


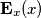 . Le formule restano comunque quelle cose piuttosto lunghe. Il grafico che devo fare è soltanto uno, sì, ma non so come vedere a occhio l'andamento, se sale come parabola, con che concavità, ecc... per ognuno dei 4 tratti
. Le formule restano comunque quelle cose piuttosto lunghe. Il grafico che devo fare è soltanto uno, sì, ma non so come vedere a occhio l'andamento, se sale come parabola, con che concavità, ecc... per ognuno dei 4 tratti 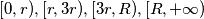 lungo l'asse x.
lungo l'asse x.

 e
e 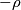 , il campo all'interno della cavità, somma vettoriale dei due campi, entrambi inversamente proporzionali alle distanze dai rispettivi centri, risulta vettorialmente costante in tutta la cavità, con componente non nulla solo lungo x.
, il campo all'interno della cavità, somma vettoriale dei due campi, entrambi inversamente proporzionali alle distanze dai rispettivi centri, risulta vettorialmente costante in tutta la cavità, con componente non nulla solo lungo x.



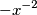 e questa è già un'ottima cosa
e questa è già un'ottima cosa  e
e  .
.
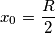 . I tuoi sono più generali e vanno sicuramente meglio.
. I tuoi sono più generali e vanno sicuramente meglio.