Già che ci siamo, per completezza e visto che se n'è parlato nei messaggi precedenti, proviamo anche a risolvere il problema con i diagrammi spazio-tempo.
In nero, nel diagramma sopra, sono rappresentati gli assi del sistema non accentato, quello in cui la barra è in quiete. Sull'asse dei tempi c'è il prodotto

. Per semplicità, ho posizionato gli estremi della sbarra in

e

: le rette azzurre rappresentano le linee d'universo di questi due estremi nel sistema in cui la barra è in quiete.
Innanzitutto, come vengono visti dal sistema di riferimento non accentato gli assi coordinati del riferimento accentato? Gli assi del riferimento accentato, hanno equazione

(asse dei tempi) e

(asse delle ascisse). Per l'asse dei tempi, per l'equazione di Lorentz, si ha

da cui

Questa è l'equazione rappresentativa dell'asse dei tempi

, come viene visto nel sistema non accentato (in altra maniera, è la traccia che l'asse dei tempi del sistema accentato lascia nel sistema non accentato): è una retta, rappresentata in rosso nel diagramma sopra, inclinata rispetto all'asse

di un angolo

tale che

Per l'asse delle ascisse si ha

da cui

Questa è l'equazione rappresentativa dell'asse delle ascisse

come viene visto nel sistema non accentato: è una retta, sempre rappresentata in rosso nel diagramma sopra, inclinata rispetto all'asse

dell'angolo

.
Volendo misurare la lunghezza della barra nel sistema accentato, dobbiamo determinare la posizione delle estremità della sbarra nello stesso istante di tempo

. In questo diagramma, le curve di equazione

sono tutte rette parallele a quella di equazione

, cioè all'asse delle ascisse rosso. Per semplicità, allora, immaginiamo di fare la misura proprio in

, come segnato nel diagramma sopra. I due punti azzurri corrispondono alle intersezioni delle due linee d'universo delle estremità della barra con l'asse

e nel sistema accentato hanno ascisse

e

da determinarsi (e questa, al prossimo post).
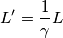 allora non dovrebbe essere vero che
allora non dovrebbe essere vero che ![\[\bigtriangleup x^{,}=\gamma \bigtriangleup x\] \[\bigtriangleup x^{,}=\gamma \bigtriangleup x\]](/forum/latexrender/pictures/d3959c8688a92cf9a69acaa6f06670c4.png) o forse non sono la stessa cosa? o è sbagliato come le intendo io? Sbaglio se dico che questa equazione serve a ricavare la lunghezza
o forse non sono la stessa cosa? o è sbagliato come le intendo io? Sbaglio se dico che questa equazione serve a ricavare la lunghezza 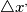 nel sistema che si muove rispetto all'oggetto da misurare, partendo dalla lunghezza
nel sistema che si muove rispetto all'oggetto da misurare, partendo dalla lunghezza 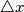 misurata nel sistema in cui l'oggetto appare fermo?
misurata nel sistema in cui l'oggetto appare fermo?
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

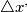 nel sistema che si muove rispetto all'oggetto da misurare, partendo dalla lunghezza
nel sistema che si muove rispetto all'oggetto da misurare, partendo dalla lunghezza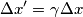 non sono la stessa cosa. Cerchiamo di capire perché.
non sono la stessa cosa. Cerchiamo di capire perché.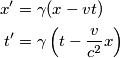
 al tempo
al tempo  (questa roba la chiamiamo,
(questa roba la chiamiamo,  al tempo
al tempo  .
. e
e 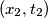 . In base alle equazioni sopra abbiamo
. In base alle equazioni sopra abbiamo![\Delta x^\prime = x_2^\prime-x_1^\prime = \gamma\left[x_2-x_1-v(t_2-t_1)\right] = \gamma(\Delta x - v\Delta t) \Delta x^\prime = x_2^\prime-x_1^\prime = \gamma\left[x_2-x_1-v(t_2-t_1)\right] = \gamma(\Delta x - v\Delta t)](/forum/latexrender/pictures/c6e77752b9535b264f31342033a50c50.png)
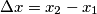 e
e 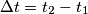 .
. 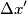 è la distanza
è la distanza 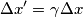 vale solo quando
vale solo quando  , cioè quando i due eventi sono simultanei nel sistema
, cioè quando i due eventi sono simultanei nel sistema  instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.
 e
e  , e le due lampadine vengono accese
, e le due lampadine vengono accese 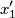 e
e  con
con 
 . Per semplicità, ho posizionato gli estremi della sbarra in
. Per semplicità, ho posizionato gli estremi della sbarra in  e
e  : le rette azzurre rappresentano le linee d'universo di questi due estremi nel sistema in cui la barra è in quiete.
: le rette azzurre rappresentano le linee d'universo di questi due estremi nel sistema in cui la barra è in quiete. (asse dei tempi) e
(asse dei tempi) e  (asse delle ascisse). Per l'asse dei tempi, per l'equazione di Lorentz, si ha
(asse delle ascisse). Per l'asse dei tempi, per l'equazione di Lorentz, si ha

 , come viene visto nel sistema non accentato (in altra maniera, è la traccia che l'asse dei tempi del sistema accentato lascia nel sistema non accentato): è una retta, rappresentata in rosso nel diagramma sopra, inclinata rispetto all'asse
, come viene visto nel sistema non accentato (in altra maniera, è la traccia che l'asse dei tempi del sistema accentato lascia nel sistema non accentato): è una retta, rappresentata in rosso nel diagramma sopra, inclinata rispetto all'asse  tale che
tale che


 sono tutte rette parallele a quella di equazione
sono tutte rette parallele a quella di equazione  e
e  da determinarsi (e questa, al prossimo post).
da determinarsi (e questa, al prossimo post). (è l'ipotenusa di un triangolo di cui
(è l'ipotenusa di un triangolo di cui 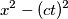 è invariante, ovvero
è invariante, ovvero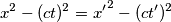
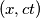 le curve di equazione
le curve di equazione 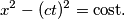 sono delle iperboli e poiché la costante è invariante, vengono chiamate
sono delle iperboli e poiché la costante è invariante, vengono chiamate  .
.
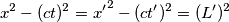
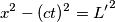
 , nel punto di ascissa
, nel punto di ascissa 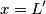 . Questo punto di intersezione è mostrato nel diagramma sopra e, come si può vedere, si ha
. Questo punto di intersezione è mostrato nel diagramma sopra e, come si può vedere, si ha 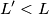 . Anche graficamente, si riottiene la contrazione delle lunghezze. Insomma, le iperboli invarianti servono da "righello" per il sistema accentato.
. Anche graficamente, si riottiene la contrazione delle lunghezze. Insomma, le iperboli invarianti servono da "righello" per il sistema accentato.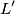 e vedere che coincide con i risultati dati in [30]
e vedere che coincide con i risultati dati in [30] 