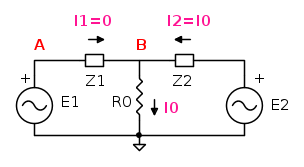
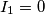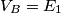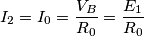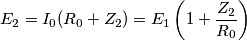Ecco i dati:




Quesiti:
A) Calcolare il valore di E2 (valore efficace e differenza di fase rispetto a E1) così che il generatore E2 non eroghi né assorba alcuna potenza (escludere il caso E2 = 0).
B) Determinare il valore di E2 (valore efficace e differenza di fase rispetto a E1) in modo che il generatore E1 non eroghi né assorba alcuna potenza; calcolare inoltre i valori massimo e minimo della potenza istantanea erogata dal generatore E2.
Sul punto A ho risolto tagliando con Thevenin inglobando tutto quello a sinistra di

Trovando una
 e un
e un 
Ora facendo il modulo del generatore equivalente ottengo

Ora non riesco a capire perché il generatore
 deve avere anch'esso questo valore efficacie per soddisfare il punto B.
deve avere anch'esso questo valore efficacie per soddisfare il punto B. Come dimostro che questo generatore non eroga ne assorbe potenza??
Per il punto C buio più totale, sono sicuro che mi sfugge qualcosa perché ci ho perso 4 ore filate di ragionamenti misti a far tornare i risultati a forza; sicuramente sbaglio totalmente approccio perché mi trovo ad avere troppe incognite per poche equazioni (in questo caso il valore efficacie di
 diventa incognito?).
diventa incognito?).Se qualche anima pia oltre a darmi un'input scontato (provaci con le potenze complesse ecc ecc) potrebbe impostarmi i passaggi sarebbe gentilissimo.
Per i temerari che ci provino ecco i risultati del quesito B:
 ,
,  ,
,  ,
, 
Colgo l'occasione anche per fare un'augurio per un buon 25 aprile!

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)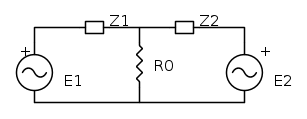

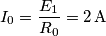
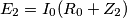
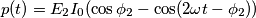
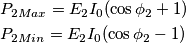


 è determinata esclusivamente da
è determinata esclusivamente da  se uno dei due generatori non fornisce ne eroga potenza significa che esso non influisce su tale tensione?
se uno dei due generatori non fornisce ne eroga potenza significa che esso non influisce su tale tensione?