quali sono i primi due termini dello sviluppo asintotico della funzione y=arcsin(x) nel punto x=1 ?
... e i primi tre?
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero
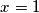 per poter avere uno sviluppo?
per poter avere uno sviluppo? 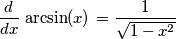
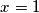 esplode, quindi direi che se l'analisi non mi ha abbandonato (che è una cosa possibilissima eheheh) non è sviluppabile (derivate inoltre non limitate ma soprattutto funzione non derivabile).
esplode, quindi direi che se l'analisi non mi ha abbandonato (che è una cosa possibilissima eheheh) non è sviluppabile (derivate inoltre non limitate ma soprattutto funzione non derivabile).RenzoDF ha scritto:quali sono i primi due termini dello sviluppo asintotico della funzione y=arcsin(x) nel punto x=1 ?
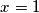 , questo non si può fare, come detto da
, questo non si può fare, come detto da ![\arcsin(1-x) = \frac{\pi}{2}-(2x)^\frac{1}{2}\left[1+\sum_{k=1}^\infty\frac{1\times 3\times 5\times\cdots\times(2k-1)}{2^{2^k}(2k+1)k!}x^k\right] \arcsin(1-x) = \frac{\pi}{2}-(2x)^\frac{1}{2}\left[1+\sum_{k=1}^\infty\frac{1\times 3\times 5\times\cdots\times(2k-1)}{2^{2^k}(2k+1)k!}x^k\right]](/forum/latexrender/pictures/8345cd8b445f7a8dd6bfc9ffae7111e3.png)
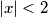 .
. instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.

DirtyDeeds ha scritto:...Il termine sviluppo asintotico è un po' ambiguo.
DirtyDeeds ha scritto:... Se intendi lo sviluppo di Taylor intorno a, questo non si può fare, come detto da
yustel.... Si possono però fare altri tipi di sviluppi ...
Simplify[ComplexExpand[Normal[Series[ArcSin[x], {x, 1, a}]]], x < 1]


 a
a  e le due costanti c perché venivano fuori numeri improponibili)
e le due costanti c perché venivano fuori numeri improponibili)

RenzoDF ha scritto:Non c'è dubbio, ma "quella" era la domanda, che non è mia.
RenzoDF ha scritto:Visto però che "gli altri sviluppi" non erano di certo assunti noti, anche se non direttamente, direi che Taylor potrebbe comunque essere utilizzato.
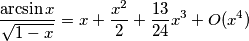
 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.

DirtyDeeds ha scritto:Non direttamente. Quello che si potrebbe fare è trovare lo sviluppo di Taylor per la funzione arcoseno divisa per un'opportuna funzione che gli rimuova la singolarità


PietroBaima ha scritto:Ecco sì, in altre parole abbiamo fatto la stessa cosa
 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.




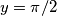 che, vista la richiesta dei soli due primi termini limito a
che, vista la richiesta dei soli due primi termini limito a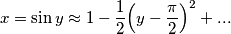


 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.

Visitano il forum: Nessuno e 7 ospiti