Perché non posso farlo?
Ah, dimenticavo di chiedere, perché non è asintotica a quella retta? Se ne calcolo il limite del rapporto viene una costante..
Diamo i numeri 2
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero
1
voti
[42] Re: Diamo i numeri 2
Ianero ha scritto:Perché non posso farlo?
perché trovi una ovvietà.
Trovi il fatto che quella funzione è compresa tra... se stessa e poi ne fai il limite.
Questo funzionerebbe con qualunque funzione
Ianero ha scritto:Ah, dimenticavo di chiedere, perché non è asintotica a quella retta? Se ne calcolo il limite del rapporto viene una costante..
Sto già scrivendo
Tra un po' ho finito...
-

 PietroBaima
PietroBaima
90,7k 7 12 13 - G.Master EY

- Messaggi: 12207
- Iscritto il: 12 ago 2012, 1:20
- Località: Londra
0
voti
[43] Re: Diamo i numeri 2
perché trovi una ovvietà.
Ho solo detto che quella disuguaglianza vale fino a un infinitesimo superiore a 1, perché posso ripetere correttamente per tutti questi valori la maggiorazione dell'esponenziale.
Non vedo l'ovvietà
Perché i ragionamenti che ci sono in quel passaggio sono errati?
Sto già scrivendo
Ti ringrazio :)
9
voti
[44] Re: Diamo i numeri 2
Il problema della soluzione di limiti per funzioni implicite è un problema annoso, rompiscatole e maledettamente necessario in fisica, che barba.
Per risolvere questo tipo di limiti, un metodo generale è quello delle funzioni speciali.
Una è la funzione Gamma di Stirling, per generalizzare il fattoriale, ne parleremo asap in "Diamo i numeri 3", magari mi ci metto domani. Ma ce ne sono molte altre.
Quando bisogna risolvere funzioni implicite non esplicitabili, trascendenti o che comunque non conviene esplicitare (spesso anche per questioni di comportamento numerico) conviene utilizzare una qualche funzione speciale. Ce ne sono molte.
Scegliere quella giusta è come scegliere l'anguria buona al mercato, non puoi essere sicuro della tua scelta, ma puoi cercare di intuire...
Nei casi in cui la parte che da fastidio è un esponenziale, come in questo caso, in genere conviene utilizzare la W di Lambert.
Questa funzione, che chiameremo W(z) è definita così:

Ho messo z perché questa funzione è estendibile al campo complesso. E' una funzione molto utile in meccanica quantistica.
Una proprietà facile da dimostrare di questa funzione è, in campo reale, la sua confrontabilità, verso infinito, al logaritmo.
Dalla definizione:

facendo il log di entrambi i membri ho:

da cui

quindi


Ragioniamo.
Il primo membro dice che il limite deve essere finito, per cui la funzione W deve essere confrontabile al logaritmo di z oppure deve esserlo il suo logaritmo, verso infinito.
Se lo fosse il suo logaritmo l'altro addendo divergerebbe, quindi ciò non è possibile.
Deve esserlo quindi la funzione stessa.
Se lo è la funzione stessa, confrontata con il logaritmo, prenderne il logaritmo e confrontarlo con il logaritmo di zeta significa ottenere zero.
Abbiamo quindi che:

Sui testi che parlano di Lambertiane si possono trovare altre proprietà davvero interessanti.
Noi però dobbiamo calcolare:

con


Quindi


Adesso osservando l'ultima espressione che ho ricavato e confrontandola con la definizione:

posso scrivere che:

da cui ovviamente:

Quindi devo calcolare

Pongo
se allora
allora 
e il limite diventa:

dato che abbiamo ricavato che W(z) è confrontabile con log(z) per z che tende a più infinito.
Poi devo tirare scherzosamente le orecchie a Ianero
Ianero 
Se una funzione è confrontabile con un'altra non significa che è ad essa asintotica.
In questo caso voglio vedere se la nostra f(x) è asintotica ad una retta.
Devo quindi verificare che esista un asintoto obliquo ad una retta, che devo trovare.
Ricordando Analisi I, per trovare un asintoto obliquo si procede in questo modo:
Facciamo un esempio di una funzione che sembra avere un asintoto ma non ce l'ha:

Punto 1. e 2. verificati, per x che va ad infinito la funzione diverge.
Punto 3. e 4. verificati, se calcolo quel limite trovo ovviamente 1.
Punto 5. e 6. no. Se calcolo quel limite trovo che diverge. Non ci sono asintoti.
Questo succede perché la radice di x non diventa trascurabile ad infinito, ma continua a crescere, pur restando "sottomessa" alla retta.
Ecco il grafico delle due funzioni tra 0 e 1:
e tra 1milione 900 mila e 2 milioni:
Come vedi l'asintoticità è solo apparente. Infatti l'unica condizione che non si verifica è l'ultima.
Roba da tema d'esame di Analisi 1, no?
Vediamo adesso l'asintoticità della nostra f(x) ad una retta.
Dimostrare che:
 diverge è banale.
diverge è banale.

Quindi resta da calcolare:

La gara è aperta
Ciao,
Pietro.
PS: il fatto che la funzione non sia asintotica ad una retta non significa che non sia asintotica ad una parabola o a qualche altra funzione, ovviamente.
Per risolvere questo tipo di limiti, un metodo generale è quello delle funzioni speciali.
Una è la funzione Gamma di Stirling, per generalizzare il fattoriale, ne parleremo asap in "Diamo i numeri 3", magari mi ci metto domani. Ma ce ne sono molte altre.
Quando bisogna risolvere funzioni implicite non esplicitabili, trascendenti o che comunque non conviene esplicitare (spesso anche per questioni di comportamento numerico) conviene utilizzare una qualche funzione speciale. Ce ne sono molte.
Scegliere quella giusta è come scegliere l'anguria buona al mercato, non puoi essere sicuro della tua scelta, ma puoi cercare di intuire...
Nei casi in cui la parte che da fastidio è un esponenziale, come in questo caso, in genere conviene utilizzare la W di Lambert.
Questa funzione, che chiameremo W(z) è definita così:

Ho messo z perché questa funzione è estendibile al campo complesso. E' una funzione molto utile in meccanica quantistica.
Una proprietà facile da dimostrare di questa funzione è, in campo reale, la sua confrontabilità, verso infinito, al logaritmo.
Dalla definizione:

facendo il log di entrambi i membri ho:

da cui

quindi


Ragioniamo.
Il primo membro dice che il limite deve essere finito, per cui la funzione W deve essere confrontabile al logaritmo di z oppure deve esserlo il suo logaritmo, verso infinito.
Se lo fosse il suo logaritmo l'altro addendo divergerebbe, quindi ciò non è possibile.
Deve esserlo quindi la funzione stessa.
Se lo è la funzione stessa, confrontata con il logaritmo, prenderne il logaritmo e confrontarlo con il logaritmo di zeta significa ottenere zero.
Abbiamo quindi che:

Sui testi che parlano di Lambertiane si possono trovare altre proprietà davvero interessanti.
Noi però dobbiamo calcolare:

con


Quindi


Adesso osservando l'ultima espressione che ho ricavato e confrontandola con la definizione:

posso scrivere che:

da cui ovviamente:

Quindi devo calcolare

Pongo

se
 allora
allora 
e il limite diventa:

dato che abbiamo ricavato che W(z) è confrontabile con log(z) per z che tende a più infinito.
Poi devo tirare scherzosamente le orecchie a
Se una funzione è confrontabile con un'altra non significa che è ad essa asintotica.
In questo caso voglio vedere se la nostra f(x) è asintotica ad una retta.
Devo quindi verificare che esista un asintoto obliquo ad una retta, che devo trovare.
Ricordando Analisi I, per trovare un asintoto obliquo si procede in questo modo:
- bisogna calcolare
 ;
; - se il limite è infinito si passa al punto seguente, altrimenti non c'è asintoto;
- bisogna calcolare
 ;
; - se questo limite è finito e non nullo (chiamiamo questo valore m) significa che la funzione è confrontabile con una retta e si passa al punto successivo, altrimenti non c'è asintoto;
- bisogna calcolare
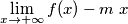 , se questo limite è finito (chiamiamo questo valore q) la funzione f(x) ha un asintoto obliquo a
, se questo limite è finito (chiamiamo questo valore q) la funzione f(x) ha un asintoto obliquo a 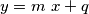 altrimenti non c'è asintoto.
altrimenti non c'è asintoto.
Facciamo un esempio di una funzione che sembra avere un asintoto ma non ce l'ha:

Punto 1. e 2. verificati, per x che va ad infinito la funzione diverge.
Punto 3. e 4. verificati, se calcolo quel limite trovo ovviamente 1.
Punto 5. e 6. no. Se calcolo quel limite trovo che diverge. Non ci sono asintoti.
Questo succede perché la radice di x non diventa trascurabile ad infinito, ma continua a crescere, pur restando "sottomessa" alla retta.
Ecco il grafico delle due funzioni tra 0 e 1:
e tra 1milione 900 mila e 2 milioni:
Come vedi l'asintoticità è solo apparente. Infatti l'unica condizione che non si verifica è l'ultima.
Roba da tema d'esame di Analisi 1, no?
Vediamo adesso l'asintoticità della nostra f(x) ad una retta.
Dimostrare che:
 diverge è banale.
diverge è banale.
Quindi resta da calcolare:

La gara è aperta
Ciao,
Pietro.
PS: il fatto che la funzione non sia asintotica ad una retta non significa che non sia asintotica ad una parabola o a qualche altra funzione, ovviamente.
-

 PietroBaima
PietroBaima
90,7k 7 12 13 - G.Master EY

- Messaggi: 12207
- Iscritto il: 12 ago 2012, 1:20
- Località: Londra
1
voti
[45] Re: Diamo i numeri 2
Ianero ha scritto:Perché i ragionamenti che ci sono in quel passaggio sono errati?
Prova a scambiare i due limiti...
-

 PietroBaima
PietroBaima
90,7k 7 12 13 - G.Master EY

- Messaggi: 12207
- Iscritto il: 12 ago 2012, 1:20
- Località: Londra
0
voti
[46] Re: Diamo i numeri 2
PietroBaima ha scritto:Roba da tema d'esame di Analisi 1
Infatti, nella comune parabola conica

la pendenza tende ad infinito ma non c'è alcun asintoto verticale (invece c'è un punto di tangenza con la retta all'infinito del piano)
3
voti
[47] Re: Diamo i numeri 2
EcoTan ha scritto:PietroBaima ha scritto:Prova a scambiare a caso le tre righe che ho evidenziato in rosso.
Ho provato, non cambia nulla.
Urca, non mi ricordavo più che l'epsilon di macchina del qbasic fosse così modesto.
Per provare la mia supposizione ho replicato il tuo programma in Mathematica, con questo codice:
- Codice: Seleziona tutto
y[n_] := 1 - 8^-n
f[a_] := Table[{N[y[n],
a], (N[y[n], a] - 1)*(N[y[n], a] - 1)/(Cos[Pi/2/N[y[n], a]])*(Tan[
Pi/2*N[y[n], a]])}, {n, 1, 10}]
Il parametro a forza la precisione di macchina ad arrestarsi ad un certo numero di cifre significative.
Con 5,10 e 13 cifre significative si ottiene:
Hai problemi di epsilon di macchina, l'algoritmo numerico diverge.
-

 PietroBaima
PietroBaima
90,7k 7 12 13 - G.Master EY

- Messaggi: 12207
- Iscritto il: 12 ago 2012, 1:20
- Località: Londra
0
voti
[48] Re: Diamo i numeri 2
Non è che ho capito tanto bene. Nel quickBasic non mi pare che ci sia il parametro a per forzare la precisione di macchina, ho soltanto definito alcune variabili in doppia precisione (floating con 64 bit, ritengo) aggiungendo un carattere # al nome della variabile. Poi ho provato, come tu mi hai suggerito, a cambiare l'ordine con cui faccio le operazioni per calcolare la funzione, ed ho notato, anche con una certa sorpresa, che di tutte quelle cifre che compaiono nella tabella non ne cambia nessuna. Questo non mi pare proprio che sia un difetto! (il limite della funzione per x tendente ad uno, deve venire correttamente zero, o no?)
Invece approfitto di questo post per fare un po' di retromarcia sulla faccenda della parabola. La pendenza della curva c'entra poco, per cercare gli asintoti bisogna esaminare il rapporto e non la derivata, come giustamente hai scritto nella condizione numero 4.
Invece approfitto di questo post per fare un po' di retromarcia sulla faccenda della parabola. La pendenza della curva c'entra poco, per cercare gli asintoti bisogna esaminare il rapporto e non la derivata, come giustamente hai scritto nella condizione numero 4.
Ultima modifica di  EcoTan il 2 lug 2014, 22:57, modificato 1 volta in totale.
EcoTan il 2 lug 2014, 22:57, modificato 1 volta in totale.
6
voti
[49] Re: Diamo i numeri 2
Chapeau  PietroBaima!
PietroBaima! 


Un altro modo veloce di trovare il limite, ma che contiene un certo numero di aspetti delicati, è il seguente. Sia , si ha
, si ha
![\frac{f(x)}{x}=\frac{a}{x}\exp\left[x\frac{1-bf(x)/x}{c}\right] \frac{f(x)}{x}=\frac{a}{x}\exp\left[x\frac{1-bf(x)/x}{c}\right]](/forum/latexrender/pictures/79f565e00b9f23e54fb2c607a8a744ee.png)
Adesso assumiamo che il limite cercato esista finito e denotiamolo con ; assumiamo anche
; assumiamo anche  sia una funzione continua, almeno nella regione di interesse. Se
sia una funzione continua, almeno nella regione di interesse. Se  , per la continuità delle funzioni coinvolte, si può scrivere
, per la continuità delle funzioni coinvolte, si può scrivere
![L = \lim_{x\rightarrow\infty}\frac{a}{x}\exp\left[x\frac{1-bL}{c}\right] L = \lim_{x\rightarrow\infty}\frac{a}{x}\exp\left[x\frac{1-bL}{c}\right]](/forum/latexrender/pictures/3e7fe5df58583273ff11169db27d840a.png)
Avendo assunto , la frazione
, la frazione  è diversa da zero: se tale frazione è positiva, l'esponenziale diverge e il limite al secondo membro non può essere finito; viceversa, se tale frazione è negativa, l'esponenziale è decrescente e il limite al secondo membro è nullo.
è diversa da zero: se tale frazione è positiva, l'esponenziale diverge e il limite al secondo membro non può essere finito; viceversa, se tale frazione è negativa, l'esponenziale è decrescente e il limite al secondo membro è nullo.
Quindi, se con le assunzioni scritte sopra,

esiste finito, o vale o vale 0.
o vale 0.



Un altro modo veloce di trovare il limite, ma che contiene un certo numero di aspetti delicati, è il seguente. Sia
 , si ha
, si ha![\frac{f(x)}{x}=\frac{a}{x}\exp\left[x\frac{1-bf(x)/x}{c}\right] \frac{f(x)}{x}=\frac{a}{x}\exp\left[x\frac{1-bf(x)/x}{c}\right]](/forum/latexrender/pictures/79f565e00b9f23e54fb2c607a8a744ee.png)
Adesso assumiamo che il limite cercato esista finito e denotiamolo con
 ; assumiamo anche
; assumiamo anche  sia una funzione continua, almeno nella regione di interesse. Se
sia una funzione continua, almeno nella regione di interesse. Se  , per la continuità delle funzioni coinvolte, si può scrivere
, per la continuità delle funzioni coinvolte, si può scrivere ![L = \lim_{x\rightarrow\infty}\frac{a}{x}\exp\left[x\frac{1-bL}{c}\right] L = \lim_{x\rightarrow\infty}\frac{a}{x}\exp\left[x\frac{1-bL}{c}\right]](/forum/latexrender/pictures/3e7fe5df58583273ff11169db27d840a.png)
Avendo assunto
 , la frazione
, la frazione  è diversa da zero: se tale frazione è positiva, l'esponenziale diverge e il limite al secondo membro non può essere finito; viceversa, se tale frazione è negativa, l'esponenziale è decrescente e il limite al secondo membro è nullo.
è diversa da zero: se tale frazione è positiva, l'esponenziale diverge e il limite al secondo membro non può essere finito; viceversa, se tale frazione è negativa, l'esponenziale è decrescente e il limite al secondo membro è nullo.Quindi, se con le assunzioni scritte sopra,

esiste finito, o vale
 o vale 0.
o vale 0.It's a sin to write  instead of
instead of  (Anonimo).
(Anonimo).
...'cos you know that ain't
ain't  , right?
, right?
You won't get a sexy tan if you write in lieu of
in lieu of  .
.
Take a log for a fireplace, but don't take for
for  arithm.
arithm.
 instead of
instead of  (Anonimo).
(Anonimo)....'cos you know that
 ain't
ain't  , right?
, right?You won't get a sexy tan if you write
 in lieu of
in lieu of  .
.Take a log for a fireplace, but don't take
 for
for  arithm.
arithm.-

 DirtyDeeds
DirtyDeeds
55,9k 7 11 13 - G.Master EY

- Messaggi: 7012
- Iscritto il: 13 apr 2010, 16:13
- Località: Somewhere in nowhere
2
voti
[50] Re: Diamo i numeri 2
EcoTan ha scritto:Non è che ho capito tanto bene. Nel quickBasic non mi pare che ci sia il parametro a per forzare la precisione di macchina, ho soltanto definito alcune variabili in doppia precisione (floating con 64 bit, ritengo) aggiungendo un carattere # al nome della variabile. Poi ho provato, come tu mi hai suggerito, a cambiare l'ordine con cui faccio le operazioni per calcolare la funzione, ed ho notato, anche con una certa sorpresa, che di tutte quelle cifre che compaiono nella tabella non ne cambia nessuna. Questo non mi pare proprio che sia un difetto! (il limite deve venire correttamente zero, o no?)
Io sono anni che non uso più il qbasic, e non mi ricordo più molto, purtroppo.
Il limite deve fare
 (confronta il post [2]).
(confronta il post [2]).Il fatto che tu non ottenga alcun cambiamento scambiando quelle righe potrebbe essere anche un brutto segno, non necessariamente un buon segno.
Per esempio anche quando c'è cancellazione numerica si ottengono dei problemi di questo tipo, anche difficili da identificare.
Se noti le ridotte tendono a fuggire da
 , che, numericamente vale circa -0.405
, che, numericamente vale circa -0.405Guarda l'implementazione dell'algoritmo su mathematica, vedrai che l'algoritmo è forzato a partire prima di quel valore, poi lo oltrepassa e ovviamente finisce nel buco nero dell'eps, quindi va verso zero.
Se guardi il tuo algoritmo vedrai che le ridotte sono già in direzione dello zero, indice di un ridotto eps di macchina.
EcoTan ha scritto:Invece approfitto di questo post per fare un po' di retromarcia sulla faccenda della parabola. La pendenza della curva c'entra poco, per cercare gli asintoti bisogna esaminare il rapporto e non la derivata, come giustamente hai scritto nella condizione numero 4.
Vorrei farti fare retromarcia sulla retromarcia.
Il limite:

è successivo alla verifica che vuole

per cui è una forma indeterminata del tipo infinito su infinito.
Applicando De l'Hopital viene quindi fuori che il limite

è equivalente a:

-

 PietroBaima
PietroBaima
90,7k 7 12 13 - G.Master EY

- Messaggi: 12207
- Iscritto il: 12 ago 2012, 1:20
- Località: Londra
Chi c’è in linea
Visitano il forum: Nessuno e 5 ospiti

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

 pigreco]=π
pigreco]=π
