ElectroYou - la comunità dei professionisti del mondo elettrico

da **Wed_17** » 31 dic 2008, 14:32

Ciao a tutti
ho il seguente circuito:

: esempio6vi8.png (2.67 KiB) Osservato 3313 volte

la rete è a riposo per t<0 e l'interruttore è aperto. A t=0 l'interruttore viene chiuso. Devo ricavare le due correnti che scorrono nei due induttori.
Ho impostato il sistema con le equazioni differenziali e sono arrivato ad un'equazione differenziale di terzo grado con incognita iL1. Per l'equazione omogenea non ci sono problemi.
Non so però in che forma devo cercare la soluzione particolare, perché questo circuito non ammette soluzione per iL1 in regime stazionario in quanto c'è un generatore di tensione in corto

come posso procedere??
Grazie a tutti

da **g.schgor** » 31 dic 2008, 16:32

Un "trucco" potrebbe essere quello (adottato nei simulatori in questi casi)
di introdurre, al posto dell'interruttore, una resistenza fittizia e piccolissima
(es. 10^(-6)ohm) che permette di superare l'ostacolo riscontrato.

da **Wed_17** » 31 dic 2008, 17:49

Non ho capito bene come funzioni: perché se io introduco uan resistenza piccolissima, e riffaccio il sistema completamente, ritrovo una nuova equaizone differenziale sempre di terzo grado, la cui soluzione particolare di iL1, risulta essere una costante. Ma questa costante, oltre a essere stata introdotta "volutamente", non soddisfa l'equazione differenziale che ho senza imporre quella resistenza, non so se mi sono spiegato. Quindi come devo procedere??
Inoltre, vedendo che sono giunto a questa equazione d^3/dt^3 iL1+10^6 d/dt iL1=2*10^6, posso scrivere che la soluzione particolare ha questa forma: iL1p=At dove A è una costante che vado a determinare dall'equazione e in questo caso risulta essere 2???

da **g.schgor** » 1 gen 2009, 10:35

Purtroppo non sono un matematico e non ti posso aiutare nella soluzione
dell'eq. differenziale. Ho anche tentato la strada di Laplace, ma non ho
raggiunto un risultato concreto.
Se ti puo' aiutare, posso dirti che la soluzione dovrebbe essere una tensione
ai capi di L1C1 di valore meta' di Vs1( quindi 5V), oscillante a ca 5kHz
modulata in ampiezza da una frequenza di ca 330Hz (escursione di ca +/- 0.2V)

da **Wed_17** » 1 gen 2009, 14:28

Ho trovato i risultati e viene

Grazie dell'aiuto

da **RenzoDF** » 1 gen 2009, 15:10

Ciao wed_17

... stavo proprio leggendo il tuo post ... un circuito interessante .

Ci racconti come hai fatto per favore :?:

Direi anzi che potresti scrivere un articolo sull'argomento ... sarebbe utile per molti ... io per primo.

Renzo

da **Wed_17** » 1 gen 2009, 16:20

Hai trovato la persona sbagliata, non vorrei passare per uno bravo in elettrotecnica...

Comuqnue posto volentieri il procedimento: innanzitutto i valori in figura sono completamente messi a caso. I valori che ho utilizzato per arrivare alla soluzione sono: L1=15mH, L2=30mH, C1=0.1mF, E=90mV. Sappiamo che la rete è a riposo per t<0 e l'interruttore è aperto. Per t=0 l'interruttore si chiude; le richieste sono le espressioni delle correnti negli induttori. Si suppone inoltre che tutte le grandezze siano continue per t=0.
Possiamo subito determinare le condizioni iniziali dal testo, e dire che per t<0: iL1=iL2=0 e Uc=0. Sapendo che le grandezze sono continue posso scrivere:iL1(0-)=iL1(0+)=iL2(0-)=iL2(0+)=0 e Uc(0-)=Uc(0+)=0.
Ora possiamo passare allo studio per t>0.
Impostiamo subito le equazioni di Kirchhoff e le leggi di bipolo e le mettiamo a sistema (premetto che è la prima volta che uso LaTex e non so fare il sistema):
$E=U_{L1}+U_{L2}, U_{L1}=U_{C1}, i_{E}=i_{L1}+i_{C1}, U_{L2}=L_{2}\frac{d}{dt}i_{E}, U_{L1}=L_{1}\frac{d}{dt}i_{L1}, i_{C1}=C_{1}\frac{d}{dt}U_{C1}$
ora sostituiamo le leggi di bipolo nelle equazioni di Kirchhoff, e arriviamo al seguente sistema, e dopo qualche sostituzione arriaviamo alla seguente equazione differenziale non omogena di terzo grado con la sola incognita iL1:
$\frac{d^3}{dt^3}i_{L1}+(\frac{L_1+L_2}{C_1L_1L_2})\frac{d}{dt}i_{L1}=\frac{E}{C_1L_1L_2}$
La soluzione sarà data dalla somma della soluzione omogena e di una soluzione particolare:
$i_{L1}(t)=i_{L1o}+i_{L1p}$ .
Sostituendo i numeri, troviamo l'equaizone caratteristica, che è:
s^3+10^6s=0

le cui soluzioni sono s_1=0

e $s_{2,3}=+-1000j$
La soluzione omogenea avrà quindi la forma $i_{L1o}=Bcos(1000t)+Dsin(1000t)$ dove B e D sono costanti da determinare imponendo le condizioni iniziali (ho messo D invece di C per non confonderlo col condensatore).
Dall'equazione differenziale possiamo vedere che si può cercare la soluzione particolare nella forma:
$i_{L1p}=At$ dove A è possibile determinarla direttamente dall'equaizone differenziali sostituendo a iL1, iL1p, ottenendo quindi 10^6A=2*10^6

->

.
All'istante t=0 sappiamo che iL1=0 quindi imponendo ciò abbiamo:
$i_{L1}(t)=i_{L1o}+i_{L1p}=At+Bcos(1000t)+Dsin(1000t)$ -> t=0 B=0

.
Adesso bisogna sfruttare le altre condizioni inziali, e sapendo che:
$U_{C1}=L1\frac{d}{dt}i_{L1}=L_1\frac{d}{dt}[Bcos(1000t)+Dsin(1000t)+At]=L_1*(1000*D*cos(1000t)+2)$ ->t=0-> 0=L_1(1000D+2)

->D=-2*10^(-3).
Ora possiamo scrivere l'espressione di iL1:
$i_{L1}(t)=-2*10^{-3}sin(1000t)+2t$
La iL2 la si può trovare sostituendo l'espressione appena trovata nel primo sistema.
Spero sia corretto e comprensibile

da **RenzoDF** » 1 gen 2009, 16:25

L'equazione differenziale per la corrente sulla L1, come tu hai gia trovato, dovrebbe essere del tipo
$\frac{{d^3 i}} {{dt^3 }} + a^2 \frac{{di}} {{dt}} = b$

ho interpretato bene?

$\left( {ho\,\,scritto\,\,a^2 \,\,per\,\,convenienza\,\,di\,\,calcolo } \right)$

Per non trovarmi una radice quadrata fra i piedi risolvendo in letterale .
E quindi la soluzione finale del tipo: (AVEVO pure SBAGLIATO ... che scarso che sono)

$i(t) = - \frac{b} {{a^3 }}\sin (at) + \frac{b} {{a^2 }}t$

io ho posto
$\begin{gathered}a^2 = \frac{{L_1 + L_2 }}{{C \cdot L_1 \cdot L_2 }} \hfill \\b = \frac{{V_{s1} }} {{C \cdot L_1 \cdot L_2 }} \hfill \\ \end{gathered}$

dimmi se ho sbagliato ancora qualcosa.

.... vedo che mi hai anticipato

) BRAVO

da **RenzoDF** » 1 gen 2009, 16:29

Direi proprio che con il LAVORO che hai fatto ci vuole proprio un articolo!

Che ne dici Zeno ?

Lo convinci tu :?:

Veramente in gamba wed !!!! =D>

... te lo dice un "vecchio" dell'elettrotecnica!

Renzo

da **Wed_17** » 1 gen 2009, 17:03

Ih dio grazie troppi complimenti :oops:

Approfitto della tua conoscenza per la risoluzione di questo circuito che allego.

Il circuito è in regime sinusiodale, i valori sono quelli indicati in figura e per il generatore di corrente risulta:
J(t)=J_Msin(Wt+A)=18*sin(1500t+pi/2)

La rete è in regime sinusoidale per t<0, variabili sempre continue alla chiusura dell'interruttore, trovare le espressioni temporali di Uc, iL1 e della corrente iT nel corto.
Sto cercando l'espressione di Uc, e l'equazione caratteristica mi viene:
s^2+150*s+10^5=0

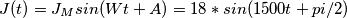
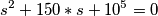mentre la soluzione scrive s^2+200*s+10^5=0

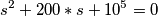e non capisco dove sbaglio

: esempio7ql2wed_17.png (2.97 KiB) Osservato 3157 volte

ElectroYou - la comunità dei professionisti del mondo elettrico

Circuito in Regime Variabile

[1] Circuito in Regime Variabile

[2] Re: Circuito in Regime Variabile

[3] Re: Circuito in Regime Variabile

[4] Re: Circuito in Regime Variabile

[5] Re: Circuito in Regime Variabile

[6] Re: Circuito in Regime Variabile

[7] Re: Circuito in Regime Variabile

[8] Re: Circuito in Regime Variabile

[9] Re: Circuito in Regime Variabile

[10] Re: Circuito in Regime Variabile

Chi c’è in linea

Informazioni

Seguici

Pubblicità

Credits