(Esercizio) Sfera Isolante e Guscio Metallico

[EdmondDantes]

Dal Mazzoldi - Nigro:
"Le proprietà dei conduttori in equilibrio possono essere riassunte dicendo che la carica di un conduttore si distribuisce sempre sulla sua superficie (ok) in modo tale che il campo elettrostatico generato da essa e da altre cariche eventualmente presenti sia nullo all'interno del conduttore".

Il Mazzoldi-Nigro-Voci tratta anche il conduttore cavo e lo schermo elettrostatico. Hai studiato quel paragrafo?

[MrEngineer]

Certamente. Ma può anche darsi che io abbia travisato qualcosa, per carità!

[EdmondDantes]

E gli esempi svolti con tutti gli andamenti dei potenziali e dei campi E (presenti nel paragrafo)?
Credo che sia abbastanza chiaro quel paragrafo.

Hai la possibilita' di prendere in prestito altri libri di fisica?

[IsidoroKZ]

Nel disegno che hai fatto, mi pare che ci sia campo dentro al guscio, cosa che non puo` essere.

Provo a partire dal principio. Guscio e sfera, ambedue metallici, hanno cariche Q1 e Q2 (Q1 e Q2 possono essere sia positive che negative, uguali o diverse...). I due oggetti sono molto lontani, non interagiscono, le due cariche sono tutte sulle superfici esterne. Dentro al buco non c'e` campo, come si vede dalla superficie gaussiana rossa dato che dentro non c'e` carica.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Quando si mette la sferetta dentro il guscio mi sembra che dica che si ha questa situazione della figura a sinistra, ma questo e` impossibile perche' vorrebbe dire avere campo dentro al guscio. Se guardi la superficie gaussiana rossa a destra vedi che questa contiene la carica Q2 e quindi ci dovrebbe essere campo, cosa impossibile

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Quello che succede e` che quando introduci la sfera piccola con carica Q2, sull'interno del guscio, per induzione, si localizza una carica -Q2, che cancella il campo nel guscio, e adesso la superficie di Gauss rossa tratteggiata contiene una carica +Q2-Q2=0 e quindi niente campo nel metallo, comde deve essere (figura sotto a sinistra)

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Ma questo non basta, perche' il guscio e` isolato, prima aveva carica Q1, e se deve spostare una carica -Q2 all'interno, dovendo rimanere la carica totale +Q1, sull'esterno la carica deve essere +Q1+Q2 e puoi calcolare il campo esterno con la carica Q1+Q2 e la superficie rossa solita.

Oppure puoi pensare che inizialmente avevi due cariche separate Q1 e Q2. Le metti insieme contornate dalla stessa superficie, il campo totale e` dato dalla somma delle cariche, non ti interessa come si dispongono (NB, questo puoi dimenticarlo, e` complicato).

Se ora metti un filo fra sfera e guscio, come mostrato sotto, hai che Q2 e -Q2 si annullano, e rimane solo Q1+Q2 fuori dalla sfera (figura sotto)

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

[PietroBaima]

Impossibile spiegarlo meglio di come è stato spiegato qui sopra.

[MrEngineer]

Madonna che risposta! E che grafici! Ti meriti 100 punti per l'impegno e la precisione. Il grafico che ho fatto nella pagina dietro, precisamente questo

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

si riferisce ad un altro esercizio, non vorrei aver fatto troppa confusione con le domande. In particolare, si riferisce al seguente:
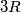"Sia dato un cilindro metallico di raggio e lunghezza su cui è distribuita una carica . Una guaina metallica cilindrica di altezza , raggio interno e spessore ) è posta coassiale al cilindro e possiede una carica ." Alla luce di quanto letto, avevo tracciato quel grafico, che è ovviamente inguardabile. Chiedo venia.

Invece, per il testo di cui sopra, quello corretto dovrebbe essere il seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Mi confermate?

[IsidoroKZ]

Non va. Se la guaina ha carica iniziale -Q, anche alla fine deve essere -Q, quindi la carica esterna della guaina deve essere....

Oppure detto diversamente se metti insieme una carica Q e una -Q la carica totale, che e` quella che conta per Gauss, vale... e quindi il campo esterno vale...

Visto che la guaina funziona da schermo, puoi anche pensare che il campo esterno sia tutto dovuto alla carica sulla superficie esterma della guaina, quindi la carica esterna vale...

Le due cose importanti da ricordare in questi esercizi sono che la carica si conserva e dentro al metallo non c'e` campo, quindi una superficie gaussiana che passa dentro al metallo include una carica totale nulla.

[MrEngineer]

Mannaggia
Se inseriamo una sfera di carica Q all'interno della cavità, sulla superficie interna della cavità si avrà per induzione una carica -Q. E su questo non ci piove. Ma se c'è una carica -Q all'interno, deve esserci una carica +Q sulla superficie esterna della guaina, che a sua volta era già carica con carica -Q. Ma se deve esserci -Q all'esterno, allora sulla superficie della guaina non dovrebbe esserci una carica -Q - Q + Q?

[PietroBaima]

Gauss nel metallo...

[MrEngineer]

Non so che dire, a questo punto mi sa che son duro io di testa. Ma a me sembrava proprio la situazione descritta qui:

Ma questo non basta, perche' il guscio e` isolato, prima aveva carica Q1, e se deve spostare una carica -Q2 all'interno, dovendo rimanere la carica totale +Q1, sull'esterno la carica deve essere +Q1+Q2 e puoi calcolare il campo esterno con la carica Q1+Q2 e la superficie rossa solita.