Buon giorno.
L'impedenza Zo di una linea di trasmissione, vista dai morsetti di alimentazione della stessa, ha, come noto, un valore costante (indipendentemente dalla lunghezza della linea stessa).
Sappiamo che Zo tiene conto della R , L, G e C per unità (m, km) e che costituiscono celle infinitesimali della linea stessa. E che di queste celle infinitesimali ce ne sono, ovviamente, un numero infinito.
Ma,chiedo,come si può impostare un'espressione matematica che tenga conto di tutto ciò e che dimostri che Zo è sempre la stessa in ogni punto?
Vi ringrazio e saluto tutti.
La Zo di una linea di trasmissione.
Moderatori: ![]() carloc,
carloc, ![]() g.schgor,
g.schgor, ![]() BrunoValente,
BrunoValente, ![]() IsidoroKZ
IsidoroKZ
33 messaggi
• Pagina 1 di 4 • 1, 2, 3, 4
0
voti
luigi_48 ha scritto:L'impedenza Zo di una linea di trasmissione, vista dai morsetti di alimentazione della stessa, ha, come noto, un valore costante (indipendentemente dalla lunghezza della linea stessa).
Achtung, questo è vero se la linea è chiusa su una impedenza uguale oppure ha lunghezza infinita.
La trattazione non la ricordo, così a orecchio mi pare che ci fosse da integrare un sistema differenziale detto "dei telegrafisti".
0
voti
Buongiorno,
Credo che tu stia cercando l'equazione dei telegrafisti :
https://www.electroyou.it/users/Sicurez ... /linee.htm
Credo che tu stia cercando l'equazione dei telegrafisti :
https://www.electroyou.it/users/Sicurez ... /linee.htm
0
voti
Grazie ragazzi per le risposte. Sì, in effetti è l'equazione dei telegrafisti che dà risposta al mio quesito. Pensavo, però, ci fosse un altro modo, magari più semplice, per arrivare alla stessa conclusione.
Ho visto di recente un esercizio di elettrotecnica così impostato:
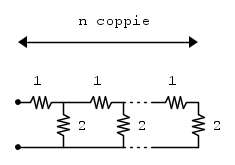
si consideri una rete elettrica costituita da una serie infinita di resistenze da 1ohm ognuna delle quali ha in parallelo una resistenza da 2ohm. Determinare il valore della resistenza equivalente di questa rete.
Per risolvere il problema bisogna dire che la resistenza equivalente è sempre la stessa in ogni punto della rete (come la Zo delle linee di trasmissione) . La resistenza equivalente è = 1ohm con in parallelo 2ohm ai quali 2ohm sta in parallelo la stessa resistenza equivalente. Ne nasce un'equazione di secondo grado il cui risultato è 2ohm (-1ohm si esclude).
E' tutto molto semplice, direi banale. Però, perché dicono che la resistenza equivalente è la stessa in tutti i punti della rete? Qual è l'espressione analitica che dimostra ciò?
Bisogna anche in questo caso ricorrere ad un'equazione simil-telegrafisti per carirlo?
E' questo che mi domando.
Ho visto di recente un esercizio di elettrotecnica così impostato:
si consideri una rete elettrica costituita da una serie infinita di resistenze da 1ohm ognuna delle quali ha in parallelo una resistenza da 2ohm. Determinare il valore della resistenza equivalente di questa rete.
Per risolvere il problema bisogna dire che la resistenza equivalente è sempre la stessa in ogni punto della rete (come la Zo delle linee di trasmissione) . La resistenza equivalente è = 1ohm con in parallelo 2ohm ai quali 2ohm sta in parallelo la stessa resistenza equivalente. Ne nasce un'equazione di secondo grado il cui risultato è 2ohm (-1ohm si esclude).
E' tutto molto semplice, direi banale. Però, perché dicono che la resistenza equivalente è la stessa in tutti i punti della rete? Qual è l'espressione analitica che dimostra ciò?
Bisogna anche in questo caso ricorrere ad un'equazione simil-telegrafisti per carirlo?
E' questo che mi domando.
1
voti
luigi_48 ha scritto:Però, perché dicono che la resistenza equivalente è la stessa in tutti i punti della rete? Qual è l'espressione analitica che dimostra ciò?
La frase:
luigi_48 ha scritto:si consideri una rete elettrica costituita da una serie infinita di resistenze da 1ohm ognuna delle quali ha in parallelo una resistenza da 2ohm
la puoi tradurre analiticamente come segue.
Costruiamo una successione
 , partendo da
, partendo da  :
: .
.La successione la definiamo poi per ricorrenza, dicendo che il termine
 è legato al precedente così:
è legato al precedente così:
che visualizzato significa che se il termine
 -esimo corrisponde a questo:
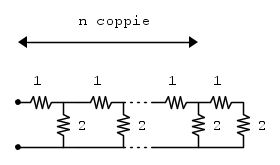
-esimo corrisponde a questo:allora il termine
 -esimo è questo:
-esimo è questo:Poiché la successione appena definita ammette limite, allora hai come immediata conseguenza che:

per qualsiasi
 , che è proprio la risposta alla tua domanda.
, che è proprio la risposta alla tua domanda.0
voti
Ianero ha scritto:la successione appena definita ammette limite
Mi stavo chiedendo se fosse possibile calcolare direttamente il limite di questa successione definita per ricorrenza
0
voti
Bella domanda! La successione non può tendere a zero perché abbiamo la prima resistenza in serie, non può tendere a infinito perché abbiamo la prima resistenza in parallelo, non può essere oscillante perché altrimenti mi arrabbio quindi deve tendere a un valore finito?
0
voti
Se per qualche motivo ci troviamo ad avere l'elemento n-esimo della successione oltre 2, allora (puoi verificarlo in un attimo):

Potrebbe oscillare? No, perché (di nuovo, si verifica in un attimo):

che è contro l'ipotesi di partenza.
Ma allora, essendo partiti con , abbiamo generato una successione decrescente e inferiormente limitata, per le quali il limite esiste per forza.
, abbiamo generato una successione decrescente e inferiormente limitata, per le quali il limite esiste per forza.

Potrebbe oscillare? No, perché (di nuovo, si verifica in un attimo):

che è contro l'ipotesi di partenza.
Ma allora, essendo partiti con
 , abbiamo generato una successione decrescente e inferiormente limitata, per le quali il limite esiste per forza.
, abbiamo generato una successione decrescente e inferiormente limitata, per le quali il limite esiste per forza.0
voti
Aggiungo una curiosità.
La rete di resistenze così costruita genera delle frazioni continue (troncate, non intere e costruite al contrario):

Vuoi vedere che [1;1/2,1,1/2,1,...] è proprio 2?
La rete di resistenze così costruita genera delle frazioni continue (troncate, non intere e costruite al contrario):

Vuoi vedere che [1;1/2,1,1/2,1,...] è proprio 2?
33 messaggi
• Pagina 1 di 4 • 1, 2, 3, 4
Chi c’è in linea
Visitano il forum: Nessuno e 66 ospiti

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)








 , allora:
, allora:
