 da
da  Ingchimico » 5 ott 2011, 11:13
Ingchimico » 5 ott 2011, 11:13
Buongiorno a tutti,sto studiando per l'esame di elettrotecnica,son arrivato alle reti trifase e non mi è chiaro un punto:sul testo dice che esiste una relazione tra tensioni concatenate e quelle stellate,e fin qui ci sono.Ad esempio sono note queste relazioni:



Ora io mi chiedo,se ad esempio mi occorre la tensione concatenata

,ed ho a disposizione la tensione stellata

,come mi devo muovere?Come ottengo tutte le possibili combinazioni tra tensioni stellate e concatenate? Spero di aver espresso in maniera chiara il mio dubbio

.Grazie a chi risponderà.



 ,ed ho a disposizione la tensione stellata
,ed ho a disposizione la tensione stellata  ,come mi devo muovere?Come ottengo tutte le possibili combinazioni tra tensioni stellate e concatenate? Spero di aver espresso in maniera chiara il mio dubbio
,come mi devo muovere?Come ottengo tutte le possibili combinazioni tra tensioni stellate e concatenate? Spero di aver espresso in maniera chiara il mio dubbio 
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

 , devi ricavare
, devi ricavare 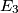 , sapendo che questa è in anticipo rispetto alla prima di 120° (o se vuoi in ritardo di 240°). La loro differenza ti darà la tensione concatenata
, sapendo che questa è in anticipo rispetto alla prima di 120° (o se vuoi in ritardo di 240°). La loro differenza ti darà la tensione concatenata 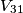 .
.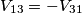


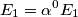

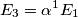
 e
e 
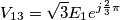 ?
? ,
,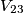 ,
,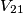 ,
,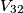 ,
,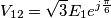

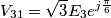
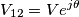
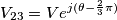

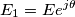
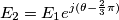
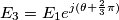
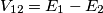
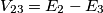
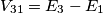
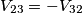
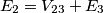
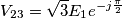 ,ma non riesco a capire il perché..
,ma non riesco a capire il perché..



