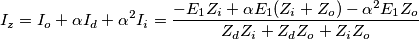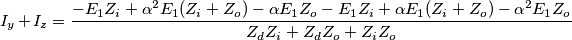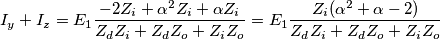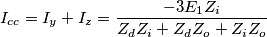da
da  admin » 10 nov 2011, 16:06
admin » 10 nov 2011, 16:06
pot ha scritto:[..]
(-j3^1/2 En (Zo-aZi))/ZdZo+ZoZi+ZiZo scusate ma non so inserire le formule con latex

Non è una scusa valida:
si deve imparare, ci sono strumenti che facilitano, come indicato negli articoli di Help. Non si capisce perché tu voglia infliggere di interpretare le formule senza fare il minimo sforzo per collaborare con chi è disposto ad aiutarti, nel caso conosca l'argomento. (Tra l'altro la formula che hai scritto è pure sbagliata: cosa facilissima da ottenere scrivendo le formule in quel modo).
-----
Il guasto è il seguente
Le condizioni di guasto permettono di stabilire che

quindi di impostare il seguente sistema per le componenti di sequenza delle tensioni e delle correnti

Tale sistema corrisponde al parallelo dei tre bipoli di sequenza, quindi allo schema
Si possono ora ricavare le correnti di sequenza

Quindi le correnti di guasto valgono:

e poiché si ha


si ottiene

---

e poiché

si può scrivere anche

-----
Infine si ha

(che in fondo è una verifica essendo la corrente sul neutro il triplo della componente omopolare)

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)




















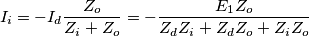
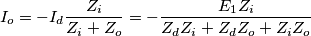
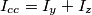
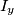 da:
da: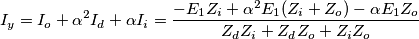
 da:
da: