Si in effetti sto trovando serie difficoltà..comunque nella rappresentazione del primario è disegnata sul mio testo un'impedenza

, percorsa dalla corrente

nel ramo trasversale con ai capi la tensione primaria a vuoto

. Bah..Comunque è vero, ho capito benissimo quello che mi hai detto sulla corrente a vuoto e quella che dovrebbe essere la vera rappresentazione. Piuttosto fatico ancora a capire alcune cose:
1) la f.e.m. indotta può essere scelta arbitrariamente
nel suo verso ai capi dell' induttore primario? E così anche per la corrente e la f.e.m. indotta ai capi dell'induttore secondario? Non si tiene conto del senso degli avvolgimenti? Cioè: una volta scelto il verso delle correnti nel primario e nel secondario, il verso della f.e.m. indotta non dipende da essi in base al senso degli avvolgimenti?
2) Il circuito secondario che ho disegnato è quello che il mio testo riporta non come circuito semplificato, ma come circuito che rende conto del funzionamento vero e proprio, senza trascurare l'effetto della corrente a vuoto.. Non capisco però come si passa da questa situazione al primario:

a questa al secondario:

3) Non capisco perché, nella rappresentazione del primario,

. Il rapporto non dovrebbe essere semplicemente uguale al rapporto spire, essendo quello un trasformatore ideale?
4) Non capisco come si trovano i parametri (tensioni e correnti) riportati al secondario. Cioè:

Ho visto la spiegazione di
 lillo
lillo ma non capisco dove vogliono arrivare i primi passaggi. Ho capito benissimo invece, il passaggio al secondario dell'impedenza a vuoto.
P.S.: il mio testo è un misto di appunti scritti a mano dal professore e capitoli di un libro di cui non conosco né titolo né autore.
Grazie!

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



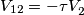 , dove
, dove  è il rapporto spire.
è il rapporto spire. 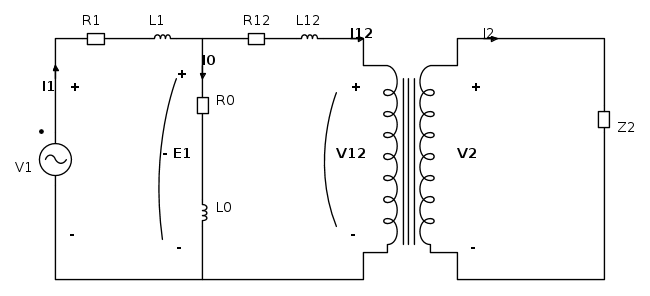
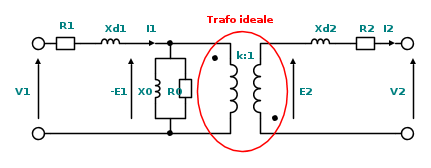
 . Per svolgere correttamente questa trasformazione, è utile ricordare che l'impedenza "vista" dai morsetti primari di un trasformatore ideale risulta essere...
. Per svolgere correttamente questa trasformazione, è utile ricordare che l'impedenza "vista" dai morsetti primari di un trasformatore ideale risulta essere...
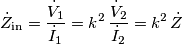

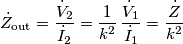




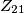 , si fanno delle considerazioni energetiche sulla potenza dissipata e si arriva a trovare la relazione
, si fanno delle considerazioni energetiche sulla potenza dissipata e si arriva a trovare la relazione 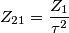 . Tutto questo considerando un' approssimazione fondamentale:
. Tutto questo considerando un' approssimazione fondamentale: 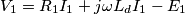
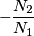 :
: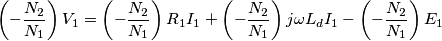
 per
per 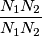 :
: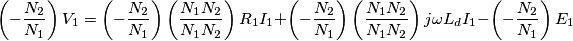
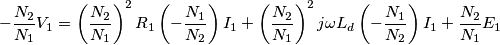
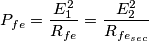
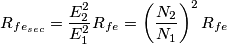
 induttanza magnetizzante:
induttanza magnetizzante: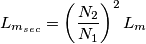

 , percorsa dalla corrente
, percorsa dalla corrente  nel ramo trasversale con ai capi la tensione primaria a vuoto
nel ramo trasversale con ai capi la tensione primaria a vuoto  . Bah..Comunque è vero, ho capito benissimo quello che mi hai detto sulla corrente a vuoto e quella che dovrebbe essere la vera rappresentazione. Piuttosto fatico ancora a capire alcune cose:
. Bah..Comunque è vero, ho capito benissimo quello che mi hai detto sulla corrente a vuoto e quella che dovrebbe essere la vera rappresentazione. Piuttosto fatico ancora a capire alcune cose:

 . Il rapporto non dovrebbe essere semplicemente uguale al rapporto spire, essendo quello un trasformatore ideale?
. Il rapporto non dovrebbe essere semplicemente uguale al rapporto spire, essendo quello un trasformatore ideale? 

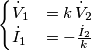
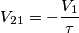 . Cioè la tensione pr. riportata al sec. è uguale a meno il rapporto tra quella primaria e il rapporto spire.
. Cioè la tensione pr. riportata al sec. è uguale a meno il rapporto tra quella primaria e il rapporto spire.
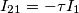
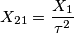
 , cioè il rapporto tra le tensioni a vuoto è uguale al rapporto spire.
, cioè il rapporto tra le tensioni a vuoto è uguale al rapporto spire.