Gentilmente heeelp grazie!!!
Traccia:
Il circuito in figura è a riposo per
 . Determinare l'andamento nel tempo della tensione del condensatore
. Determinare l'andamento nel tempo della tensione del condensatore  .
.Dati del problema:
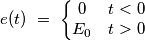
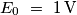
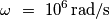

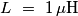
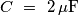
Circuito:
Moderatori: ![]() carloc,
carloc, ![]() g.schgor,
g.schgor, ![]() BrunoValente,
BrunoValente, ![]() IsidoroKZ
IsidoroKZ
 . Determinare l'andamento nel tempo della tensione del condensatore
. Determinare l'andamento nel tempo della tensione del condensatore  .
.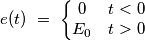
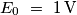
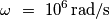

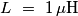
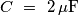


Glorietta ha scritto:Grazie ancora e perdonate la scrittura delle formule un po' elementare...prima o poi diventerò pratica ;)
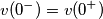 e
e 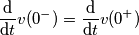 .
.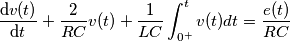


angelsanct ha scritto:...ricordando che......



 per trovare una delle due costanti di indeterminazione.
per trovare una delle due costanti di indeterminazione.  , applichi
, applichi  per calcolare l'ultima costante di indeterminazione ed è fatta
per calcolare l'ultima costante di indeterminazione ed è fatta 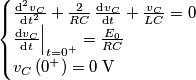
![\[v_C=\frac{{\text{e}}^{-250000\,t}\,\mathrm{sin}\left( 250000\,\sqrt{7}\,t\right) }{\sqrt{7}}\] \[v_C=\frac{{\text{e}}^{-250000\,t}\,\mathrm{sin}\left( 250000\,\sqrt{7}\,t\right) }{\sqrt{7}}\]](/forum/latexrender/pictures/83199874d5f54462936517fdc5b0a31c.png)


Visitano il forum: Nessuno e 52 ospiti