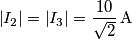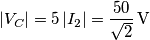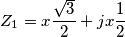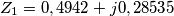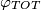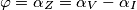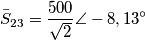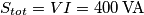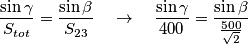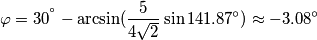Nel circuito in figura sono noti:




Sapendo che l'impedenza
 è ohmico-induttiva con angolo caratteristico di 30° determinare:
è ohmico-induttiva con angolo caratteristico di 30° determinare:• la corrente di ciascun ramo;
• la tensione ai capi del parallelo;
• l'angolo di sfasamento fra corrente totale e tensione totale.
Mi sono trovato la Z equivalente del parallelo e mi esce:

Poi mi ricavo la Z totale del circuito facendo:

Da cui trovo
 :
:
Calcolo la caduta di tensione su Z1 e mi risulta uguale:

Dopodiché ho trovato la tensione ai capi del parallelo che mi risulta uguale a:

E mi sono ricavato quindi le correnti che circolano in ogni ramo che risultano entrambe di:

Fino qui i risultati mi tornano come quelli del libro ma per calcolare l'angolo di sfasamento totale tra tensione e corrente non so come fare.
Se potreste aiutarmi vi sarei molto grato.
Il risultato sul libro dice che deve risultare:
 in anticipo.
in anticipo.
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)