Volevo una conferma sulla derivata della seguente funzione composta:
^{2}} y=\sqrt[3](x+1)^{2}}](/forum/latexrender/pictures/b5c6e3a94870a6a5382b1cfdf1fb67f5.png)
(è tutto sotto la radice)
la sua derivata è questa?
![y'=\frac{1}{3\sqrt[3]{(x+1)^{2}}}\cdot 2(x+1)1 y'=\frac{1}{3\sqrt[3]{(x+1)^{2}}}\cdot 2(x+1)1](/forum/latexrender/pictures/ec530c4db2106c5d0ac2edabc5cf4497.png)
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero
^{2}} y=\sqrt[3](x+1)^{2}}](/forum/latexrender/pictures/b5c6e3a94870a6a5382b1cfdf1fb67f5.png)
![y'=\frac{1}{3\sqrt[3]{(x+1)^{2}}}\cdot 2(x+1)1 y'=\frac{1}{3\sqrt[3]{(x+1)^{2}}}\cdot 2(x+1)1](/forum/latexrender/pictures/ec530c4db2106c5d0ac2edabc5cf4497.png)


![y=\sqrt[3]{\left(x+1\right)^{2}}=\left(x+1\right)^{\frac{2}{3}} y=\sqrt[3]{\left(x+1\right)^{2}}=\left(x+1\right)^{\frac{2}{3}}](/forum/latexrender/pictures/3e675f8c69aa1ee145f1b226fd0683e3.png)
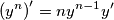
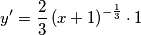



palliit ha scritto:E' sbagliata.
 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.



GustaVittorio ha scritto:
PietroBaima ha scritto:


![y'=\frac{2(x+1)}{3\sqrt[3]{((x+1)^{2})^{3-1}}}=\frac{2(x+1)}{3\sqrt[3]{(x+1)^{4}}} y'=\frac{2(x+1)}{3\sqrt[3]{((x+1)^{2})^{3-1}}}=\frac{2(x+1)}{3\sqrt[3]{(x+1)^{4}}}](/forum/latexrender/pictures/9616237fe81e64fc89baeaf1df5316a7.png)


GustaVittorio ha scritto:Se volessi procedere secondo il mio metodo allora pongo una correzione :
 dentro la radice e semplificarlo con quello al numeratore...Ti verrebbe fuori il risultato calcolato con il metodo della potenza...Di solito infatti si preferisce usare il metodo con la potenza perché è di più facile risoluzione e dà un risultato pressoché già "semplificato"
dentro la radice e semplificarlo con quello al numeratore...Ti verrebbe fuori il risultato calcolato con il metodo della potenza...Di solito infatti si preferisce usare il metodo con la potenza perché è di più facile risoluzione e dà un risultato pressoché già "semplificato"Visitano il forum: Nessuno e 6 ospiti