lo schema rappresenta un tratto infinitesimo di linea, facente parte di una cascata di quadripoli a
 .
.prendendo in considerazione il tratto infinitesimo rappresentato e considerando la retta delle ascisse come riferimento dello spazio, prendiamo come verso positivo quello che va dall'arrivo alla partenza;
vogliamo studiare l'evolversi del circuito, non più solo in funzione del tempo, come l'elettrotecnica classica insegna, ma anche in funzione dello spazio:
applicando le leggi di Kirchhoff al quadripolo possiamo scrivere:

ora qualche semplificazione:
![\left\{\begin{matrix}
v(x,t)+\frac{\partial v(x,t)}{\partial x}\mathrm{d}x-v(x,t)=ri(x,t)\mathrm{d}x+r\frac{\partial i(x,t)}{\partial x}\mathrm{d}x\mathrm{d}x+l\frac{\partial }{\partial t}\left [i(x,t)\mathrm{d}x+\frac{\partial i(x,t)}{\partial x}\mathrm{d}x \mathrm{d}x \right ]\\
i(x,t)+\frac{\partial i(x,t)}{\partial x}\mathrm{d}x-i(x,t)=gv(x,t)\mathrm{d}x+c\frac{\partial v(x,t)}{\partial t}\mathrm{d}x
\end{matrix}\right. \left\{\begin{matrix}
v(x,t)+\frac{\partial v(x,t)}{\partial x}\mathrm{d}x-v(x,t)=ri(x,t)\mathrm{d}x+r\frac{\partial i(x,t)}{\partial x}\mathrm{d}x\mathrm{d}x+l\frac{\partial }{\partial t}\left [i(x,t)\mathrm{d}x+\frac{\partial i(x,t)}{\partial x}\mathrm{d}x \mathrm{d}x \right ]\\
i(x,t)+\frac{\partial i(x,t)}{\partial x}\mathrm{d}x-i(x,t)=gv(x,t)\mathrm{d}x+c\frac{\partial v(x,t)}{\partial t}\mathrm{d}x
\end{matrix}\right.](/forum/latexrender/pictures/ba4448cef5b1d1634118956ba221f964.png)
trascuriamo gli infinitesimi di ordine superiore al primo, e semplifichiamo per ottenere:

ovvero le equazioni dei telegrafisti.
tali equazioni sono valide per qualsiasi forma d'onda in ingresso al quadripolo, con ipotesi di linearità del circuito.
in condizioni di regime sinusoidale le equazioni possono essere così riscritte:

con:


quindi otteniamo:

deriviamo adesso la prima, ovvero la (1.1), rispetto a x:

ma dalla (1.2) vediamo che:

da cui ricaviamo:

e procedendo analogamente con la seconda, abbiamo il nuovo sistema:

nell'ultimo sistema abbiamo introdotto la seguente quantità:

definita come la costante di propagazione della linea.
K è complesso e quindi può essere scritto come:

con:


 causa per l'appunto l'attenuazione del modulo delle grandezze dalla partenza all'arrivo, mentre
causa per l'appunto l'attenuazione del modulo delle grandezze dalla partenza all'arrivo, mentre  lo sfasamento delle stesse all'arrivo rispetto alla partenza.
lo sfasamento delle stesse all'arrivo rispetto alla partenza.le (2.1) e (2.2) sono equazioni differenziali del second'ordine e come tali ammettono soluzioni del tipo

in realtà le soluzioni linearmente indipendenti sono solo due, essendo
 e
e  soluzioni anche di:
soluzioni anche di:
sostituiamo nella (1.1) le soluzioni trovate in (3.1):

ma dalle (1) risulta anche:

e uguagliando i coefficienti otteniamo:


e individuiamo:

con
 impedenza d'onda della linea.
impedenza d'onda della linea.il sistema quindi diventa:

e per trovare le costanti k1 e k2 dobbiamo imporre le condizioni ai limiti:
risparmiandoci l'intero svolgimento giungiamo a:

attraverso le equazioni appena scritte, noi possiamo conoscere tensione e corrente in qualsiasi punto della linea attraverso la conoscenza delle grandezze all'arrivo
le parti sottolineate sono mie affermazioni e sarei grato a chiunque me ne desse conferma.
ovviamente sono ben accette correzioni di qualsiasi tipo.
3D un po' pesante, quindi ringrazio chiunque lo legga fino alla fine.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)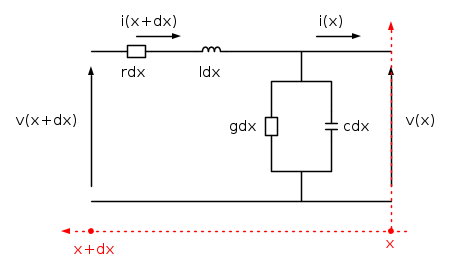





 ma con lunghezza longitudinale (usualmente in funzione della coordinata
ma con lunghezza longitudinale (usualmente in funzione della coordinata  ) che
) che 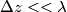 in cui le variabili di stato tensione e corrente sono funzioni della coordinata spaziale
in cui le variabili di stato tensione e corrente sono funzioni della coordinata spaziale 
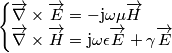
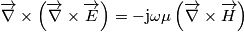
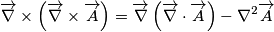
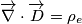
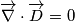
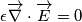

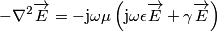
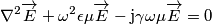
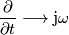
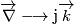

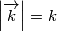
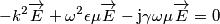
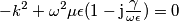
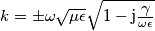
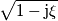
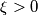 , poiché
, poiché 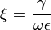
![\sqrt{1-\mathrm{j}\xi}=\frac{1}{\sqrt{2}}\left[\sqrt{\sqrt{1+\xi^{2}}+1}-\mathrm{j}\sqrt{\sqrt{1+\xi^{2}}-1}\right] \sqrt{1-\mathrm{j}\xi}=\frac{1}{\sqrt{2}}\left[\sqrt{\sqrt{1+\xi^{2}}+1}-\mathrm{j}\sqrt{\sqrt{1+\xi^{2}}-1}\right]](/forum/latexrender/pictures/62f18ec870a3a6a3fc922d9c675baf1e.png)
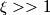
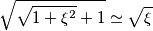
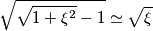
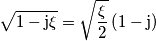
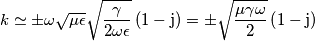
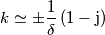

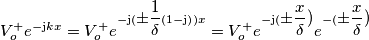

 pigreco]=π
pigreco]=π

