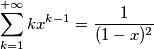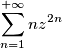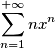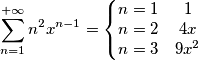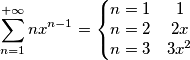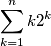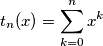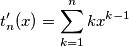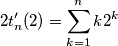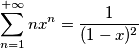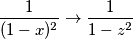Stavo provando a risolvere un esercizio in cui veniva chiesto di calcolare la trasformata z di questa funzione

Io ho provato a ragionare in questo modo

Per ottenere la z-trasformata ho fatto
![Z[a(n)\cdot u(n))]=Z_u[a(n)]=\sum_{n=0}^{3}2^{3-n}z^{-n} + \sum_{n=3}^{+\infty} 2^{n-3}z^{-n} Z[a(n)\cdot u(n))]=Z_u[a(n)]=\sum_{n=0}^{3}2^{3-n}z^{-n} + \sum_{n=3}^{+\infty} 2^{n-3}z^{-n}](/forum/latexrender/pictures/d07d5e8cb934652723b98e426d2b2c45.png)
Ora la prima serie è una serie finita di termini per cui li ho sviluppati e la seconda serie l'ho ricondotta ad una serie di potenze... ho scritto

ottenendo

Il problema è che non mi trovo con il risultato che mi da wolfram in quanto

Io penso di aver sbagliato con la serie finita perché il problema mi nasce con quel
 che mi altera l'espressione. Ho provato anche ad escludere quell'elemento ma comunque non mi trovo...
che mi altera l'espressione. Ho provato anche ad escludere quell'elemento ma comunque non mi trovo...Ora risolvere un esercizio a tentativi non è proprio il massimo della vita, vorrei capire cosa sbaglio
Vi ringrazio in anticipo per ogni aiuto! :)

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

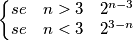
 nella definizione non è ben posta.
nella definizione non è ben posta.

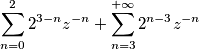
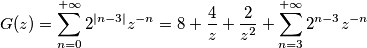
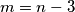
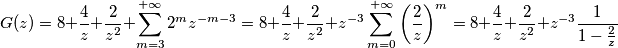
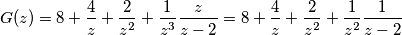
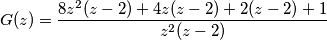
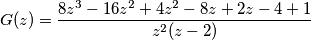
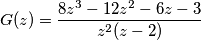
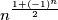

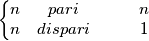
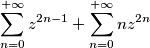
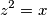 e usa la relazione
e usa la relazione