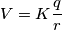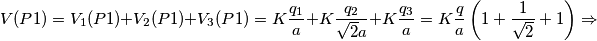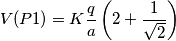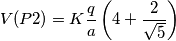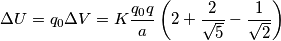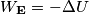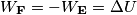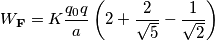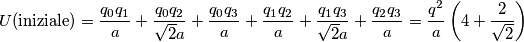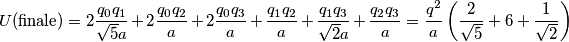Ho un problema con questo esercizio:
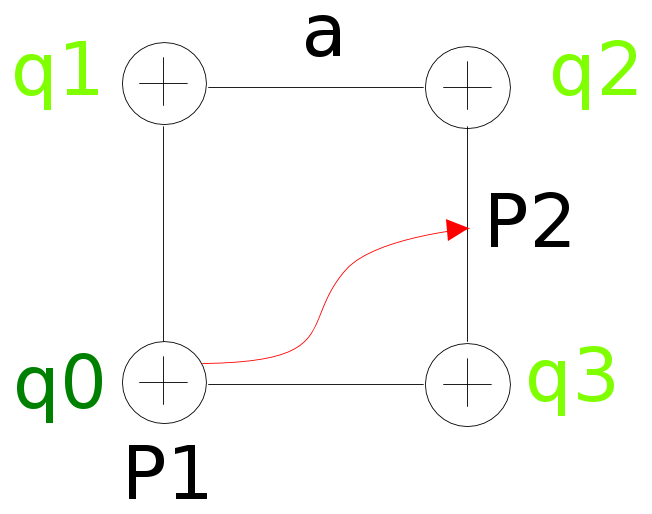
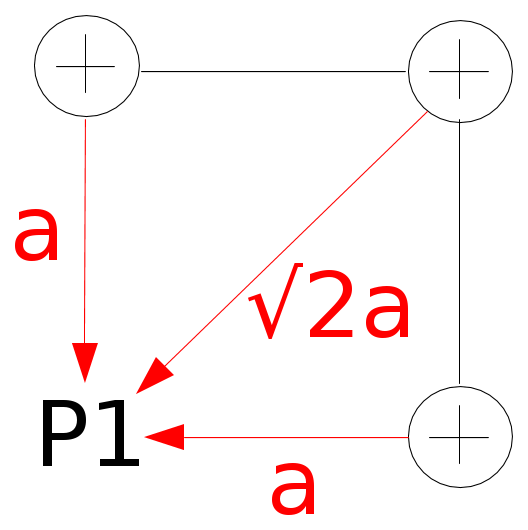
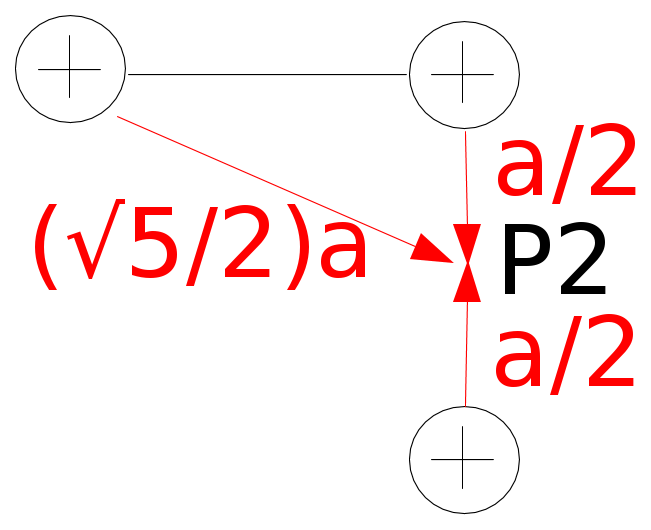
"Quattro cariche puntiformi di egual valore q=10^(−8) C sono poste ai vertici di un quadrato di lato a=10 cm. Calcolare l'energia potenziale elettrostatica del sistema e il lavoro necessario per spostare una delle cariche dalla posizione iniziale P1 al punto P2 indicato in figura e situato nel centro del lato"
Per quanto riguarda il calcolo dell'energia potenziale elettrostatica non ho problemi, mentre sul calcolo del lavoro ho una incongruenza col segno. Indicando con V il potenziale generato dalle restanti 3 cariche e con K la costante di Coulomb, trovo dopo qualche passaggio:
![W_{P_1 \rightarrow P_2} =-q[V(P_2)-V(P_1)] \Rightarrow W_{P_1 \rightarrow P_2} =-q[V(P_2)-V(P_1)] \Rightarrow](/forum/latexrender/pictures/f2d527869761bcd6a9f212b384954cf8.png)

numericamente:

I conti mi sembrano corretti, per cui vorrei sapere (tanto per togliermi il dubbio) se ho ben compreso tutte le definizioni riguardanti lavoro, energia potenziale e potenziale elettrico:



dove
 è la carica di prova,
è la carica di prova,  è il vettore campo elettrico e
è il vettore campo elettrico e  è l'energia potenziale elettrica.
è l'energia potenziale elettrica.
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)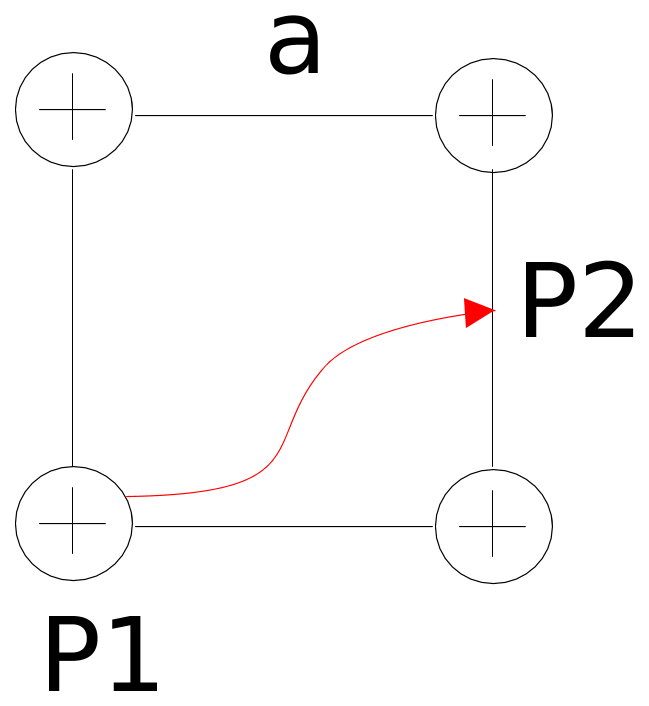


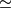 che stà ad indicare "uguaglianza asintotica", non "uguale a circa" per il quale si usa invece
che stà ad indicare "uguaglianza asintotica", non "uguale a circa" per il quale si usa invece  .
.