Sia X un insieme di numeri reali non vuoto limitato superiormente, allora X è dotato di estremo superiore.
È specificato che questo teorema vale solo per i numeri reali.
Mi sono chiesto: per quale motivo non dovrebbe valere anche per i razionali?
Se esiste comunque un insieme di maggioranti Y di X, può al massimo capitare che l'estremo superiore reale sia minore rispetto al minimo maggiorante razionale, ma questo non ne pregiudica comunque l'esistenza, come invece dice il teorema.
Mi sbaglio?

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.
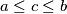


 non sarebbe comunque completo come spazio metrico.
non sarebbe comunque completo come spazio metrico.