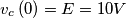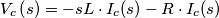Ciao a tutti vorrei sapere quali passaggi bisogna fare utilizzando la trasformata di Laplace per analizzare il seguente circuito:
Inizialmente i contatti K1 sono chiusi mentre K2 è aperto, quindi il condensatore si carica.
All'istante t=0+ i contatti di K1 si aprono e nel frattempo si chiude K2.
Dati:
E = 10 V
C = 100 mF
L = 2 H
R = 10 Ω
Devo trovare la funzione della tensione in uscita V0.
Sapreste spiegarmi che passaggi devo fare?
Analisi circuito RLC
Moderatori: ![]() g.schgor,
g.schgor, ![]() IsidoroKZ
IsidoroKZ
16 messaggi
• Pagina 1 di 2 • 1, 2
2
voti
Direi sia immediato vedere che il condensatore per t=0+ sarà carico alla tensione E del generatore mentre l'induttore sarà attraversato da una corrente nulla, ne segue che, introdotto il generatore fittizio per modellare la condizione iniziale su C, e sostituiti i bipoli con gli equivalenti secondo Laplace, si tratta di scrivere una semplice equazione di Kirchhoff alla maglia per ricavare la corrente I(s) nella stessa e di conseguenza la V0(s)=R*I(s).
Antitrasformando avrai la funzione del tempo cercata.
Ora però tocca a te fare il calcolo, poi noi controlleremo.
Antitrasformando avrai la funzione del tempo cercata.
Ora però tocca a te fare il calcolo, poi noi controlleremo.
"Il circuito ha sempre ragione" (Luigi Malesani)
3
voti








Io un generatore ce lo vedo...
-

 PietroBaima
PietroBaima
90,7k 7 12 13 - G.Master EY

- Messaggi: 12206
- Iscritto il: 12 ago 2012, 1:20
- Località: Londra
2
voti
Eneru ha scritto:Scusa puoi spiegarmi meglio cosa rappresenta il generatore fittizio e come diventerebbe il circuito aggiungendolo?
Mi sembra molto strano che tu pretenda di risolvere con Laplace senza conoscerlo, ad ogni modo
"Il circuito ha sempre ragione" (Luigi Malesani)
2
voti
Eneru ha scritto:ma quando devo risolverlo la corrente I(s) non dovrebbe andare al contrario nello stesso senso del generatore?
La convenzione per la corrente nella rete la scegli poi come più ti comoda, quello che ti ho disegnato è solo l'equivalente del bipolo che, usando la convenzione degli utilizzatori, porta alla relazione costitutiva standard per il dispositivo

"Il circuito ha sempre ragione" (Luigi Malesani)
3
voti
Eneru ha scritto:Quindi è giusto scrivere l'equazione di di Kirchhoff in questo modo:
Certo ma mi sembra più "conveniente" scegliere una corrente di maglia opposta, vista la tensione richiesta.
Io la rete la disegnerei in questo modo, dove ho lasciato indicato anche il GIT impulsivo fittizio relativo all'induttore (in questo caso nullo)
Come vedi ho scelto la corrente di maglia I(s) concorde con IL(S) e opposta alla IC(S) e, vista la semplicità della stessa, invece di Kirchhoff, userei un bel partitore di tensione.
Ad ogni modo, se posso darti un consiglio, questi GIT o GIC addizionali relativi alle condizioni iniziali devi ricordarteli a memoria, non è difficile: per il condensatore potrai scegliere fra un normale GIT serie (vc(0)/s) o un GIC impulsivo parallelo (C*v(0)) e viceversa per l'induttore con GIT impulsivo serie (L*iL(0)) o GIC parallelo (iL(0)/s).
Nel nostro caso particolare abbiamo scelto i generatori serie sempre per "convenienza", ma nel caso di una parallelo R L C sarebbe stato "conveniente" scegliere i corrispondenti generatori parallelo.
"Il circuito ha sempre ragione" (Luigi Malesani)
16 messaggi
• Pagina 1 di 2 • 1, 2
Torna a Elettrotecnica generale
Chi c’è in linea
Visitano il forum: Nessuno e 19 ospiti

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



 pigreco]=π
pigreco]=π