
In wikipedia dice inoltre che si può arrivare a questa formula partendo dalla corrente
 e tensione
e tensione  istantenee.
istantenee.Potete mostrarmi come fare, oppure darmi un indizio in più perché la non dice altro? Ve ne sono grato se mi aiutate.
Moderatori: ![]() g.schgor,
g.schgor, ![]() IsidoroKZ
IsidoroKZ

 e tensione
e tensione  istantenee.
istantenee.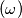 , quindi una frequenza
, quindi una frequenza  , quindi un periodo
, quindi un periodo 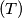 . A questo punto il concetto di istantaneità della potenza reattiva si perde.
. A questo punto il concetto di istantaneità della potenza reattiva si perde.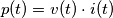 . Io fino ad oggi credo solo a questa relazione. Poi chissà cosa ci inventeremo per il futuro.
. Io fino ad oggi credo solo a questa relazione. Poi chissà cosa ci inventeremo per il futuro.
 lectroYou
lectroYourini ha scritto:Nella relazione che hai proposto compare un omega, quindi una frequenza
, quindi un periodo
. A questo punto il concetto di istantaneità della potenza reattiva si perde.[/list]
 è una costante, quindi non influenza l'intervallo di osservazione e non si perde il concetto di istantaneità.
è una costante, quindi non influenza l'intervallo di osservazione e non si perde il concetto di istantaneità.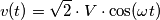

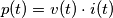
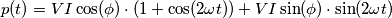
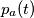 ), il secondo la potenza reattiva istantanea (
), il secondo la potenza reattiva istantanea (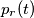 ):
):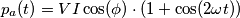
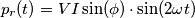
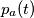 e
e 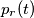 si può ricavare "sviluppando" la corrente nelle sue componenti in fase
si può ricavare "sviluppando" la corrente nelle sue componenti in fase 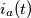 e in quadratura (
e in quadratura (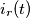 ) con la tensione:
) con la tensione: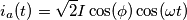
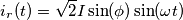
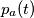 e
e 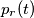 sono dunque:
sono dunque: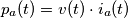
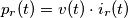

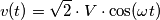

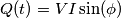 , che però è il solito valore della potenza reattiva, definito come il massimo della potenza reattiva istantanea
, che però è il solito valore della potenza reattiva, definito come il massimo della potenza reattiva istantanea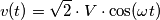


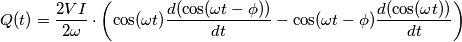
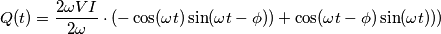
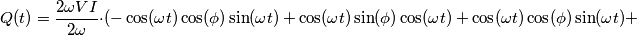

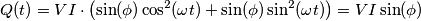
E' un errore allora.


 , dovranno essere diverse le definizioni delle potenze reattive istantenee, la qual cosa tutto sommato non è un problema, perché, come già detto da
, dovranno essere diverse le definizioni delle potenze reattive istantenee, la qual cosa tutto sommato non è un problema, perché, come già detto da  .
.


 , coerentemente con ciò che ci saremmo aspettati secondo la teoria delle potenze in regime periodico non sinusoidale, dove, secondo la teoria di Budeanu:
, coerentemente con ciò che ci saremmo aspettati secondo la teoria delle potenze in regime periodico non sinusoidale, dove, secondo la teoria di Budeanu:

Torna a Elettrotecnica generale
Visitano il forum: Nessuno e 14 ospiti