 come faccio per calcolare f(0),f(1),f(2)... ?
come faccio per calcolare f(0),f(1),f(2)... ? Quello che vorrei capire è come interpreto questo valore ?
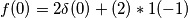
Ringrazio in anticipo
 come faccio per calcolare f(0),f(1),f(2)... ?
come faccio per calcolare f(0),f(1),f(2)... ? 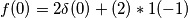

elettro1 ha scritto: come faccio per calcolare?
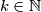 e svolgi i calcoli
e svolgi i calcoli 
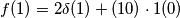

 per le funzioni continue e
per le funzioni continue e ![f[n] f[n]](/forum/latexrender/pictures/eaed2299febf5554577674f2ee2db3c2.png) per quelle a tempo discreto.
per quelle a tempo discreto. ![\delta[n] \overset{\Delta}{=}
\begin{cases}
1 & \text{se } n = 0\\
0 & \text{se } n \neq 0
\end{cases} \delta[n] \overset{\Delta}{=}
\begin{cases}
1 & \text{se } n = 0\\
0 & \text{se } n \neq 0
\end{cases}](/forum/latexrender/pictures/b7fa8c34ff3327c20ad5b216cef7c4f5.png)
Torna a Elaborazione numerica ed analogica dei segnali
Visitano il forum: Nessuno e 2 ospiti