 ma ho una serie infinita di problemi. Io l’avrei calcolata partendo dalla definizione , considerando che il periodo della funzione è pi greco e che posso integrare la funzione da pigreco a - pigreco perché oltre si ripete, avrei scritto :
ma ho una serie infinita di problemi. Io l’avrei calcolata partendo dalla definizione , considerando che il periodo della funzione è pi greco e che posso integrare la funzione da pigreco a - pigreco perché oltre si ripete, avrei scritto : 
A questo punto il mio libro mi suggerisce di applicare le formule di eulero , così dopo aver posto il seno uguale a
 mi sono bloccata. Inoltre cercando altri esercizi svolti per cercare di capire, ho visto che esercizi simili vengono però risolti con la definizione
mi sono bloccata. Inoltre cercando altri esercizi svolti per cercare di capire, ho visto che esercizi simili vengono però risolti con la definizione  e non capisco quando applicare una o l’altra. So che ho sicuramente lacune spaventose ma potreste provare ad illuminarmi
e non capisco quando applicare una o l’altra. So che ho sicuramente lacune spaventose ma potreste provare ad illuminarmi 

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

 e
e 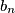 , poi eventualmente ricavando i coefficienti
, poi eventualmente ricavando i coefficienti  partendo da questi ultimi, oppure faccio il contrario.
partendo da questi ultimi, oppure faccio il contrario.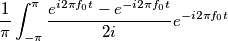



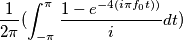 . Adesso porto fuori la i a denominatore e poi spezzo l’integrale della sottrazione , che ho a numeratore, da cui ricavo
. Adesso porto fuori la i a denominatore e poi spezzo l’integrale della sottrazione , che ho a numeratore, da cui ricavo 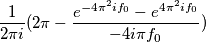
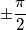 ma pigreco ?
ma pigreco ?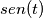 ha periodo
ha periodo 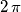 , la funzione
, la funzione 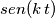 con
con  costante e reale ha il periodo di
costante e reale ha il periodo di 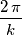 quindi nel tuo caso
quindi nel tuo caso 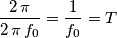 .
.


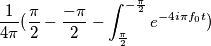 questo perché essendo la funzione sen2x ha (credo ) un periodo di 1/2pi e non di 1/pi come avevo scritto prima, inoltre ho corretto gli estremi dell’integrale che vanno da pigreco mezzi a - pigreco mezzi. Ora risolvendo gli integrali mi risulta
questo perché essendo la funzione sen2x ha (credo ) un periodo di 1/2pi e non di 1/pi come avevo scritto prima, inoltre ho corretto gli estremi dell’integrale che vanno da pigreco mezzi a - pigreco mezzi. Ora risolvendo gli integrali mi risulta 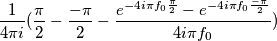 . A parte risolvere la prima parte della parentesi , poi non saprei come andare avanti
. A parte risolvere la prima parte della parentesi , poi non saprei come andare avanti