z^2 + ¡z + (1 + ¡)^8 -10 = 0
Qual è il procedimento per risolverla? Ho provato a farla parecchie volte ma mi ritrovo sempre in un punto in cui non riesco ad ottenere la forma canonica delle eqz di secondo grado.
Grazie in anticipo
Come si risolve la seguente equazione con numeri complessi?
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero
6 messaggi
• Pagina 1 di 1
0
voti
Prova ad esplicitare la parte reale ed immaginaria di z: 
e vedi cosa salta fuori.
perché ti dico di fare questo?
Se scrivo la seguente equazione nelle variabili reali :
:

con x, y, a, b numeri reali
ti è chiaro il fatto che da questa equazione ne consegue direttamente:

?

e vedi cosa salta fuori.
perché ti dico di fare questo?
Se scrivo la seguente equazione nelle variabili reali
 :
:
con x, y, a, b numeri reali
ti è chiaro il fatto che da questa equazione ne consegue direttamente:

?
"The past is not really the past until it has been registered. Or put another way, the past has no meaning or existence unless it exists as a record in the present."
John Archibald Wheeler
John Archibald Wheeler
0
voti
Perdonami ma non sono riuscito a cogliere del tutto le operazioni mostrate sopra. Però, svolgendo l' equazione
sono riuscito ad arrivare a questo punto:
z^2 + iz +32i -10 = 0
Lo scopo è trovare i valori di z per cui l'equazione è verificata. Per fare ciò necessito della forma base:
az^2 + bz + c = 0
Cosa dovrei fare? grazie in anticipo
sono riuscito ad arrivare a questo punto:
z^2 + iz +32i -10 = 0
Lo scopo è trovare i valori di z per cui l'equazione è verificata. Per fare ciò necessito della forma base:
az^2 + bz + c = 0
Cosa dovrei fare? grazie in anticipo
0
voti
Grazie veramente del suggerimento. Avevo sbagliato proprio là. Infatti ora (1+i)^8 mi viene 16 e il problema scompare.
8
voti
Secondo me questi problemi sono utili per imparare un metodo, piuttosto che per imparare a fare calcoli a testa bassa.
Il problema è questo:

cosa mi da fastidio?
Due cose:
1. la j davanti a z
2. 1+j elevato alla ottava potenza.
Partiamo dal secondo punto.
Se elevo 1+j al quadrato ottengo 2j, perché
quindi
quindi
quindi l'equazione è

adesso veniamo al primo punto, il j di fronte alla z. Raccolgo un meno e riscrivo l'equazione in questa forma:

applico quindi la formula risolutiva delle equazioni di secondo grado:


Il problema è questo:

cosa mi da fastidio?
Due cose:
1. la j davanti a z
2. 1+j elevato alla ottava potenza.
Partiamo dal secondo punto.
Se elevo 1+j al quadrato ottengo 2j, perché

quindi

quindi

quindi l'equazione è

adesso veniamo al primo punto, il j di fronte alla z. Raccolgo un meno e riscrivo l'equazione in questa forma:

applico quindi la formula risolutiva delle equazioni di secondo grado:


-

 PietroBaima
PietroBaima
90,7k 7 12 13 - G.Master EY

- Messaggi: 12206
- Iscritto il: 12 ago 2012, 1:20
- Località: Londra
6 messaggi
• Pagina 1 di 1
Chi c’è in linea
Visitano il forum: Nessuno e 0 ospiti

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



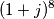

 pigreco]=π
pigreco]=π