![\lim_{x \to \infty}\frac{\sqrt[3]{1+x^{2}+2x^{\alpha }}-\cos x}{x+x^{\alpha }} \lim_{x \to \infty}\frac{\sqrt[3]{1+x^{2}+2x^{\alpha }}-\cos x}{x+x^{\alpha }}](/forum/latexrender/pictures/3f9335531e2d5fbe92d0d98ef66da862.png)
con

Il problema non è lo studio del limite, ma del suo studio legato al parametro alpha.
Sono arrivato alla soluzione (spero giusta) dell'esercizio a tentativi, dando cioè dei valori ad alpha e studiando il limite ogni volta, ma mi rendo conto che questo non è il metodo più corretto ne il più veloce.
Esistono dunque dei metodi che mi permettono di arrivare alla soluzione di limiti come questo senza dare arbitrariamente dei valori ad alpha o altri parametri che entrano in gioco?
Ad ogni modo il risultato da me trovato è:
![\frac{1}{\sqrt[3]{x^{\infty}}}\Rightarrow 0 \frac{1}{\sqrt[3]{x^{\infty}}}\Rightarrow 0](/forum/latexrender/pictures/b49ead965a276ac81748c2eeb7f6e3e6.png)
Ringrazio tutti già da ora per il tempo speso

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)
 non essendo un numero reale o naturale. Dovresti fare un limite di un limite e la cosa non viene richiesta/concessa. Prova a postare i passaggi che hai fatto :). La soluzione è più semplice di quello che ti aspetti.
non essendo un numero reale o naturale. Dovresti fare un limite di un limite e la cosa non viene richiesta/concessa. Prova a postare i passaggi che hai fatto :). La soluzione è più semplice di quello che ti aspetti.



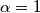
![\lim_{x\to\infty}\frac{\sqrt[3]{1-x^{2}+2x}-cosx }{x+x}\Rightarrow\lim_{x\to\infty}\frac{\sqrt[3]{x^{2}(\frac{1}{x^{2}}-1+\frac{2}{x})}-cosx }{2x} \lim_{x\to\infty}\frac{\sqrt[3]{1-x^{2}+2x}-cosx }{x+x}\Rightarrow\lim_{x\to\infty}\frac{\sqrt[3]{x^{2}(\frac{1}{x^{2}}-1+\frac{2}{x})}-cosx }{2x}](/forum/latexrender/pictures/7036ea0c405031db4649bbfaab71bcb5.png)
![\Rightarrow\lim_{x\to\infty}\sqrt[3]{\frac{x^{2}}{x}}\Rightarrow\lim_{x\to\infty}\frac{1}{\sqrt[3]x}\Rightarrow0 \Rightarrow\lim_{x\to\infty}\sqrt[3]{\frac{x^{2}}{x}}\Rightarrow\lim_{x\to\infty}\frac{1}{\sqrt[3]x}\Rightarrow0](/forum/latexrender/pictures/871d7542e749d088615100fb0daa7427.png)
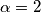
![\lim_{x \to \infty}\frac{\sqrt[3]{1+x^{2}}-cosx }{x+x^{2}}\Rightarrow\lim_{x \to \infty}\frac{\sqrt[3]{x^{2}}}{x^{2}}\Rightarrow\lim_{x \to \infty}\frac{1}{\sqrt[3]{x^{5}}}\Rightarrow0 \lim_{x \to \infty}\frac{\sqrt[3]{1+x^{2}}-cosx }{x+x^{2}}\Rightarrow\lim_{x \to \infty}\frac{\sqrt[3]{x^{2}}}{x^{2}}\Rightarrow\lim_{x \to \infty}\frac{1}{\sqrt[3]{x^{5}}}\Rightarrow0](/forum/latexrender/pictures/15b9fef8e49e39a7d606e8502ef666f1.png)
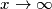
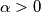
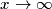
 .
.![\lim_{x \to \infty}\frac{\sqrt[3]{x^{\alpha }}}{x^{\alpha}}\Rightarrow\lim_{x \to \infty}x^{\frac{\alpha}{3}-\alpha}\Rightarrow\lim_{x \to \infty}\frac{{1}}{\sqrt[3]x^{2\alpha}}\Rightarrow0 \lim_{x \to \infty}\frac{\sqrt[3]{x^{\alpha }}}{x^{\alpha}}\Rightarrow\lim_{x \to \infty}x^{\frac{\alpha}{3}-\alpha}\Rightarrow\lim_{x \to \infty}\frac{{1}}{\sqrt[3]x^{2\alpha}}\Rightarrow0](/forum/latexrender/pictures/cd92f1c96a42008258f0f48f60cd2038.png)
![\lim_{x \to \infty}\frac{x^{\alpha /3 }\sqrt[3]{\frac{1}{x^{\alpha }}+\frac{1}{x^{\alpha-2}}+2}-\cos x}{x+x^{\alpha }}\quad \text{quando}\; \alpha\geq 2 \lim_{x \to \infty}\frac{x^{\alpha /3 }\sqrt[3]{\frac{1}{x^{\alpha }}+\frac{1}{x^{\alpha-2}}+2}-\cos x}{x+x^{\alpha }}\quad \text{quando}\; \alpha\geq 2](/forum/latexrender/pictures/f3773aff7c263f566234736dcb66e8fa.png)
![\lim_{x \to \infty}\frac{x^{2/3}\sqrt[3]{\frac{1}{x^2}+1+2\frac{1}{x^{2-\alpha }}}-\cos x}{x+x^{\alpha }}\quad \text{quando}\; \alpha<2 \lim_{x \to \infty}\frac{x^{2/3}\sqrt[3]{\frac{1}{x^2}+1+2\frac{1}{x^{2-\alpha }}}-\cos x}{x+x^{\alpha }}\quad \text{quando}\; \alpha<2](/forum/latexrender/pictures/29d8aa4bdf993c82f50e20387f8c1db8.png)
 , quindi nella seconda espressione del limite, qualunque sia
, quindi nella seconda espressione del limite, qualunque sia  , c'è già un
, c'è già un 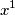 al denominatore che abolisce il numeratore, indipendentemente da chi sia il monomio più alto al denominatore. :)
al denominatore che abolisce il numeratore, indipendentemente da chi sia il monomio più alto al denominatore. :)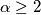 o
o 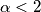 ottengo comunque un limite che tende a 0.
ottengo comunque un limite che tende a 0.