Il testo è il seguente:

Prima di vederne lo svolgimento ho provato ad eseguirlo per conto mio e, semplicemente, sono arrivato alla conclusione che questa serie converge a 0 per
 .
.Secondo i miei calcoli e passaggi otterrei infatti:

Quindi andrei a sommare valori sempre più piccoli e tendenti a
 , quindi 0.
, quindi 0.I passaggi eseguiti dall'autore del video (che ho compreso comunque senza alcun problema) portano però ad un risultato completamente opposto.
Vi espongo brevemente questi passaggi:


Sviluppando la sommatoria ottiene in fine il suo risultato:

che, chiaramente, diverge a

Il problema è che non riesco a capire cosa ci sia di sbagliato nei miei passaggi che, secondo me, hanno un senso matematico e logico.
Ringrazio tutti per il tempo speso ad aiutare me e chi può avere simili dubbi.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

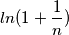 per intenderci, é infinitesimo (per
per intenderci, é infinitesimo (per 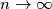 ), ma si tratta solo della verifica di una condizione necessaria, non é il risultato della somma!
), ma si tratta solo della verifica di una condizione necessaria, non é il risultato della somma!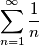 : il termine generale é infinitesimo, ma la serie diverge (serie armonica)
: il termine generale é infinitesimo, ma la serie diverge (serie armonica)

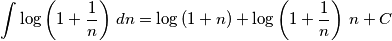


 pigreco]=π
pigreco]=π