In questo articolo si riporta lo studio basico del fenomeno del collasso di tensione nei sistemi elettrici di potenza, con la stesura dello studio elettrotecnico associato alla curva a naso della linea stessa. Si vedrà, nei diagrammi successivi, la metodologia della tracciatura della curva stessa e lo studio nei casi di collasso.
LA RETE ELETTRICA DI RIFERIMENTO
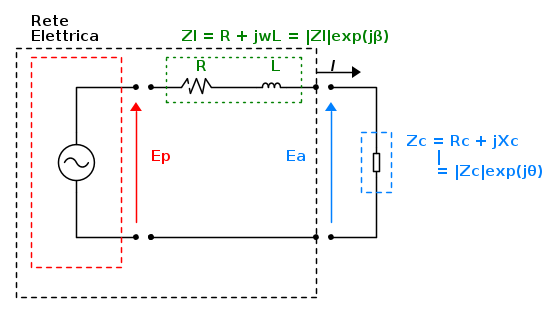
Si riporta la rete elettrica di riferimento del nostro studio del collasso di tensione.
In rosso il generatore, ed in verde l'impedenza, che rappresentano la rete elettrica equivalente (in tratteggio nero) vista dall'impedenza Zc presa in esame nel nostro studio, e studiata nel fenomeno di collasso.
Esprimiamo la tensione (è un fasore non uno scalare) ai capi del generatore di tensione sinusoidale:

Tensione ai capi dell'impedenza in esame (fasore).

Si ricava la formula della corrente I che sperimenta l'impedenza Zc:

Riscriviamo quindi Ea come:

Riarrangiamo la formula sotto radice:


La potenza elettrica assorbita dal carico Zc, si può scrivere con la seguente:

e sostituendo in essa la I, la Ea e la parentesi riscritta otteniamo:

Nel caso fossimo nella situazione di carico adattato, la condizione è:
Zc = Zl
e la potenza sarebbe così riscritta:

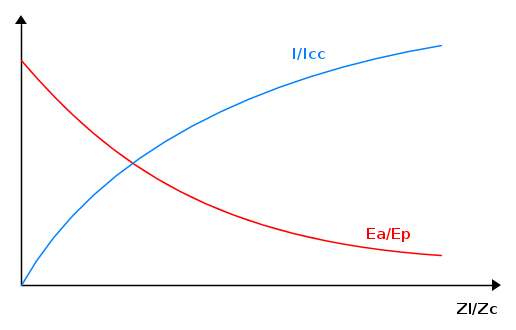
Nel diagramma successivo si vede l'andamento del rapporto I / Icc e della quota di tensione del carico Ea relativa al valore Ep della rete, in funzione dell'impedenza relativa Zl / Zc.
Si noti come il diagramma di sopra mostri come la corrente I che transita la Zc aumenti al diminuire di Zc stessa ( o se vogliamo all'aumento del rapporto Zl/Zc); viceversa per la tensione: al diminuire (RELATIVO A Zl!!!) di Zc, la tensione Ea cala relativamente sulla tensione Ep (o se vogliamo, la tensione Ea diminuisce all'aumento dell'impedenza di linea).
LA CURVA A NASO
La potenza assorbita dall'utenza Zc è, come sappiamo, sostanzialmente il prodotto di una variabile estensiva come la tensione ed una intensiva come la corrente. Molteplici sono in natura le analogie: in ogni sistema energetico o energivoro chessia si possono individuare queste due variabili, spesso denominate anche come variabile qualitativa ( tensione, entalpia, altezza geodetica, forza....) e variabile quantitativa ( corrente, portata, velocità..). Quindi, nel nostro caso, data una potenza, essa può essere data dalla combinazione di tensione e corrente, e quindi di tensione relativa (Ea/Ep) e di corrente relativa (I/Icc), riferiti entrambi alle condizioni limite Ep ed Icc (I di cortocircuito).
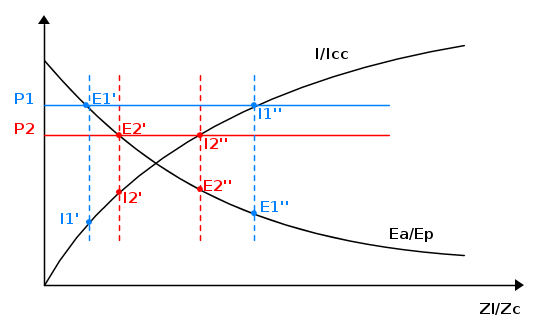
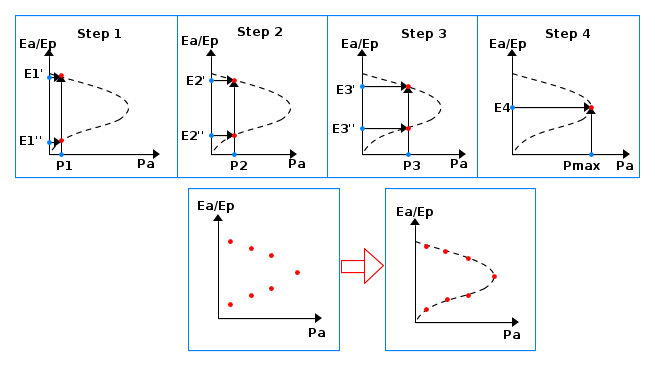
Allora possiamo avere i seguenti casi, come illustrato in figura:
Come si vede lo stesso ammontare di potenza istantaneamente assorbito o prodotto dall'utenza, può esser dato da due diversi valori di tensione e corrente.


e quindi

e così via per altri valori di potenza maggiori e minori rispettivamente di P1 e P2, ed ovviamente anche per i valori tra P1 e P2.
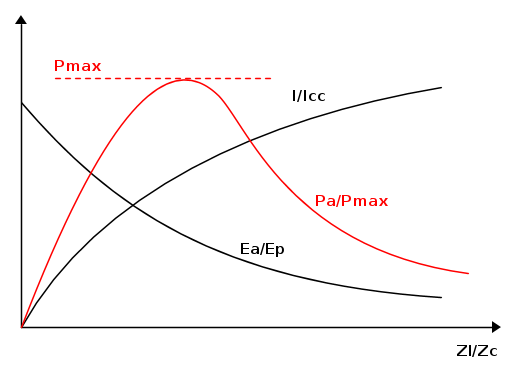
Si può così tracciare sullo stesso diagramma l'andamento della potenza assorbita/prodotta dall'utenza in funzione del rapporto Zl/Zc.
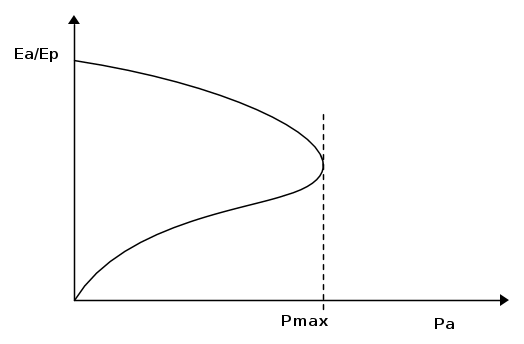
Nel successivo diagramma andiamo a tracciare la curva chiamata "a naso" per la sua forma (immagino ??), che vede il rapporto di tensione Ea/Ep vs Pa.
Ogni punto di questa curva, ossia ogni valore di potenza dell'asse delle ascisse Pa, è individuato graficamente, andando a segnare i valori di potenza relativi ad un dato valore del rapporto di tensione Ea/Ep. Quindi, per un dato Pa corrispondono due valori di Ea/Ep, tranne nel caso di Pmax, dove è unico. Da grafico alcuni esempi.
COLLASSO DI TENSIONE
Definiamo queste tipologie di utenze elettriche:
dati Po e Qo nominali, esprimiamo le potenze ( attiva e reattiva) come


e rappresentabili, con ovvio significato delle variabili, nel seguente diagramma.
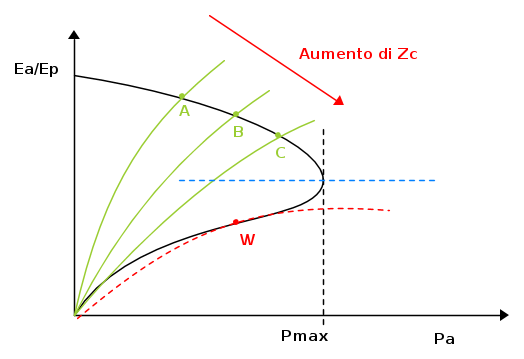
Unendo la curva a naso con la caratteristica delle utenze, supponiamo per α>1 otteniamo il seguente diagramma
Questo diagramma parla chiaro. La curva a naso è la curva del SISTEMA ELETTRICO, e assieme abbiamo la curva delle utenze (verdi e rossa). Supponiamo di lavorare nel punto A. In quel caso, il sistema fornisce una data potenza ad una data tensione Ea/Ep. Ad un aumento di impedenza vista dalla rete, ci si sposta verso il punto B e così fino al punto C, dove il sistema risponde con un aumento di potenza all'utenza a scapito di una riduzione di tensione relativa alla stessa utenza. In questi casi il sistema riesce a fornire la maggiorazione di potenza richiesta dall'utenza senza problemi. Da notare ( agli occhi dei meccanici è forse più intuibile..), che la curva a naso, nella sua parte superiore ha andamento negativo con la variabile INTENSIVA (in questo caso relativa); questo è un segnale di stabilità intrinseca del sistema. Arrivati al punto di incrocio della curva a naso con la tratteggiata blu, ci troviamo nelle condizioni in cui il sistema è alla sua massima potenza. Ad una eventuale richiesta di potenza ulteriore del carico, il sistema risponde diminuendo ancora la tensione, ma portandoci nella parte inferiore della curva, la potenza diminuisce. Il sistema collassa, in quanto, non vedendo che riesce a supplire alla richiesta di potenza, tenta di diminuire la tensione ma in questa zona ad essa corrisponde una ulteriore diminuzione di potenza (punto W). Notare come la parte instabile abbia pendenza positiva con la variabile intensiva.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)