ElectroYou - la comunità dei professionisti del mondo elettrico

Indice

1 Sintesi del procedimento
2 Dati
3 Dimensionamento preliminare
4 Avvolgimento B.T.
- 4.1 Perdite e sovratemperatura
5 Avvolgimento A.T.
- 5.1 Perdite e sovratemperatura
6 Il circuito magnetico
- 6.1 Perdite nel Ferro
- 6.2 Corrente a vuoto
7 Rendimento
8 Circuito equivalente di una fase
9 Dimensionamento del cassone
10 Bibliografia

Sintesi del procedimento

In base alla potenza si sceglie, con una formula empirica, il valore per il flusso magnetico $Φ$ .
Si fissa l'induzione massima di lavoro $B M$ , in base ai lamierini scelti, quindi si ricava la sezione necessaria del Ferro $S f e$ .
Si calcola il numero di volt per spira $E s$ con cui si stabilisce il numero di spire del secondario e del primario.
Si fissa la densità di corrente $δ$ e si dimensionano gli avvolgimenti.
Si calcolano le perdite nel rame e nel ferro ed i parametri del circuito equivalente.
Si dimensiona il cassone.

Dati

Trasformatore trifase in olio DYn a raffreddamento naturale
$S_n=630 \quad {\rm{kVA}}$
$U_1=10.500 \, {\rm{V}} \pm 500 \, {\rm{V}}$
$U_{20}=400 \, {\rm{V}}$
$f=50 \, {\rm{Hz}}$

Dimensionamento preliminare

Per un trasformatore di questo tipo si adotta la costruzione a tre colonne complanari.
La formula empirica per scegliere il flusso magnetico, espresso in weber, è

$\Phi = C \cdot \sqrt {\frac{S}{f}}$

dove $S$ è la potenza apparente del trasformatore espressa in kVA, ed $f$ la frequenza di funzionamento.
Il flusso è espresso in weber. Il coefficiente $C$ assume valori compresi tra $1 \times 10^{-2}$ ed $1,6 \times 10^{-2} \, \frac{{{\rm{V}} \cdot {\rm{s}}^{{\rm{0}}{\rm{,5}}} }}{{\rm{m}}}$ .
Un basso valore di C richiederà più spire. Il valore di C, in definitiva influenza il rapporto rame/ferro. Scegliamo $C=1,35 \times 10^{-2}$ .
Avremo
$\Phi = 1,35 \times 10^{-2} \times \sqrt {\frac{630 }{50}}=4,75 \times 10^{-2} \, {\rm{Wb}}$
Scegliendo ora per l'induzione massima un valore di $B_M=1,7 \, {\rm{T}}$ , otterremo, per il ferro, una sezione $S_{Fe}=\frac {4,75 \times 10^{-2}}{1,7}=0,028 \, {\rm{m^2}}=280 \, {\rm{cm^2}}$ .
Useremo lamierini al silicio a cristalli orientati (Terni ARMCO M6 T35)

B-H

che hanno un cifra di perdita
$C_p=0,5 \, \frac {\text{W}}{\text{kg}}$
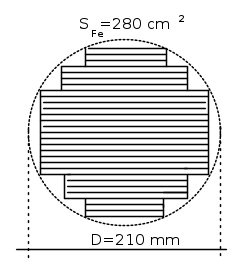
La sezione del Ferro sarà a gradini.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Realizzeremo avvolgimenti concentrici. La sezione circolare della colonna avrà un diametro $D$ ricavabile dalla equazione
$\pi \cdot \frac {D^2}{4} \cdot K_u \cdot K_s =S_{Fe}$
$K u < 1$ : coefficiente di utilizzazione perché la sezione del Ferro è a gradini;
$K s < 1$ : coefficiente di stipamento
Scegliendo $K u = 0,9$ e $K s = 0,92$ otterremo
$D=\sqrt {\frac {4 \cdot S_{Fe}}{\pi \cdot K_u \cdot K_s}}= \sqrt {\frac {4 \times 280 \cdot 10^2}{\pi \times 0,9 \times 0,92}}\approx 210 \, {\rm{mm}}$ .
Possiamo ora ricavare la tensione di ogni spira applicando la
$E_s=4,44 \times f \cdot \Phi_M$
Sostituendo in essa i valori otteniamo
$E_s=4,44 \times 50 \times 4,75 \cdot 10^{-2} = 10,5 \, {\rm{V}}$

Avvolgimento B.T.

Il numero di spire dell'avvolgimento si ricava con
$N_2=\frac {\frac {U_{20}}{\sqrt{3}}} {E_s}=\frac {230}{10,5}=22$
La corrente nominale che le deve percorrere è
$I_{2n}= \frac {S}{\sqrt{3} \cdot U_{20}}=\frac {630 \times 10^3}{\sqrt{3} \times 400}=910 \, {\rm{A}}$
A tale corrente corrisponde una forza magnetomotrice pari a
$N_2 \cdot I_{2n}=910 \times 22 = 20.000 \, {\rm{A}}$
E' il dato che serve per stabilire l'altezza dell'avvolgimento, quindi della colonna.
Una formula empirica che fornisce gli amperfili per centimetro, cioè il rapporto tra la forza magnetomotrice e l'altezza della colonna in centimetri

$A_{f,cm}=K \cdot \sqrt {\Phi_M}$

aiuta nello stabilire una altezza accettabile.
Il coefficiente K assume valori compresi tra 1500 e 3000, crescente con la potenza nominale.
Considerando un valore $K=2000 \, \frac {\rm{A}}{\rm{cm \cdot Wb^{0,5}}}$ ricaviamo
$A_{f,cm} = 2000 \times \sqrt {4,75 \times 10^{ - 2} } = 436 \, {\rm{ }}\frac{{\rm{A}}}{{{\rm{cm}}}}$
in base a cui stabiliamo l'altezza dell'avvolgimento
$h = \frac{{N_2 \cdot I_{2n} }}{{A_{f,m} }} = \frac{{910 \times 22}}{{436}} = 43,8 \to 45 \, {\rm{ cm}}$
Fissiamo ora la densità di corrente in $\delta = 3 \, \frac {\rm{A}}{\rm{mm^2}}$
Il suo valore è responsabile di perdite per effetto Joule, quindi delle sovratemperature ed in genere è compreso tra $2,5 \div 3, 5 \frac {\rm{A}}{\rm{mm^2}}$
Ricaviamo allora una sezione di rame $S_{Cu,BT}=\frac {I_{2n}}{\delta}=\frac {910}{3} \cong 300 \, {\rm{mm^2}}$
Decidiamo di distribuire l'avvolgimento, ad elica, in due strati, ciascuno di 11 spire. Dividendo l'altezza della colonna per il numero di spire di uno strato, aumentato di uno, si ottiene l'altezza di una spira, comprensiva dell'isolamento.
Dunque
$h_{sp_is,BT}=\frac {H}{11+1}=\frac {450}{12}=37,2 \, {\rm{mm}}$
Consideriamo un'altezza della spira, al netto dell'isolamento, di $h_{sp,BT}=36 \, \text{mm}$ ; la larghezza necessaria sarà $s = \frac{S}{{h_{sp,BT} }} = \frac{{300}}{{36}} = 8,33 \to 8,5{\rm{ mm}}$ .

Sezione 1

Per ridurre le perdite per correnti parassite, suddividiamo la sezione in più piattine. Ad esempio 8 piattine da $4,5 \times 8,5 \, {\text{mm}}$ , per una sezione complessiva di $S_{Cu,BT}=8 \times 4,5 \times 8,5=306 \, {\rm{mm^2}}$ (La densità di corrente non diminuisce in modo apprezzabile, quindi considereremo ancora il valore scelto)

Con la configurazione del disegno l'altezza dell'avvolgimento è
$h_{BT}=36 \times 12 = 432 \, \text{mm}$
Il diametro interno dell'avvolgimento sarà
$D_{int,BT}=D+s_{imp}+2 \cdot s_{co}=210+5+2 \cdot 6 = 227 \to 230 \, {\rm{mm}}$
$s_{imp}=5 \, \text{mm}$ è lo spessore, in mm dell'impregnamento per tenere saldo l'avvolgimento, ad esempio ottenuto con colla vinilica.
$s_{co}=6 \, \text{mm}$ è la larghezza del canale per la circolazione dell'olio tra nucleo ed avvolgimento.
Il diametro esterno sarà
$D_{ext,BT}=D_{int,BT}+2 \cdot ( 2 \cdot s_{st}+s_{coi} )=$
$=230 + 2 \times ((2 \times (4,5 +0,25 \times 2)) \times 2 + 6)=282 \, {\rm{mm}}$
$s s t$ è lo spessore di uno strato, somma dello spessore del rame e dell'isolamento in carta (0,25 mm per ogni lato della piattina).
$s c o i$ è la larghezza del canale centrale per la circolazione dell'olio tra i due strati
Il diametro medio è
$D_{medio,BT}=\frac {D_{ext,BT}+D_{int,BT}}{2}=\frac {230+282}{2}=256 \, {\rm{mm}}$

Perdite e sovratemperatura

Verifichiamo in base ai dati ottenuti le perdite nel rame dell'avvolgimento e la sua sovratemperatura rispetto all'olio

$\begin{array}{l} P_{cu,BT} = 3 \cdot R_2 \cdot I_{2n}^2 = 3 \cdot \rho _{Cu} \cdot \frac{l}{{S_{Cu,BT} }} \cdot I_{2n}^2 = \\ = 3 \cdot \rho _{Cu} \cdot \frac{{S_{Cu,BT} \cdot l}}{{S_{Cu,BT} }} \cdot \frac{{I_{2n}^2 }}{{S_{Cu,BT} }} = 3 \cdot \rho _{Cu} \cdot V_{Cu,BT} \cdot \delta ^2 = \\ = 3 \cdot \rho _{Cu} \cdot \frac{{P_{Cu,BT} }}{{p_{cu} }} \cdot \delta ^2= 3 \cdot \frac{{\rho _{Cu,75^{\circ}} }}{{p_{Cu} }} \cdot P_{Cu,BT} \cdot \delta ^2 \\ \end{array} \, [1]$

$\rho _{Cu,75^{circ}}$ : resistività del rame alla temperatura di riferimento di $75^\circ C \to 0,0213 \times 10^{-6} \, \Omega \cdot {\rm{m}}$

$p C u$ : peso specifico del rame $= 8,9 \times 10^3 \, \frac {\rm{kg}}{\rm{m^3}}$

$\frac{{\rho _{Cu,75^\circ } }}{{p_{Cu} }} = \frac{{0,0213 \times 10^{ - 6} }}{{8,9 \times 10^3 }} = 0,24 \times 10^{ - 11} {\rm{ }}\frac{{\Omega \cdot {\rm{m}}^4 }}{{{\rm{kg}}}}$

$P C u, B T$ : peso del rame dell'avvolgimento secondario

$V C u, B T$ : volume dell'avvolgimento secondario

$\begin{array}{l} P_{Cu,BT}=V_{Cu,BT} \cdot p_{Cu}= \pi \cdot D_{medio,BT} \cdot N_2 \cdot S_{Cu,BT} \cdot p_{Cu}= \\ =\pi \times 0,256 \times 22 \times 3,06 \times 10^{-4} \times 8,9 \times 10^3 = 48,2 \, {\rm{kg}}\\ \end{array}$

$P_{Cu,BT}=3 \cdot 0,24 \times 10^{ - 11} \times 48,2 \times 3^2 \times 10^{12}=3123 \, {\rm{W}}$

Nota: Si può ovviamente porre $k_p=2,4 \, \frac {\Omega \cdot \text{mm}^4}{kg}$ ed usare

$P_{Cu}=k_p \cdot peso_{Cu} \cdot \delta^2$ per calcolare le perdite nel rame nota densità di corrente in $\frac{A}{\text{mm}^2}$ e peso in

k g

La superficie disperdente totale dell'avvolgimento è costituita da 4 superfici cilindriche, avendo predisposto un canale di raffreddamento tra i due strati e vale

$S_{D,BT} = 4 \cdot \pi \cdot D_{medio,BT} \cdot h_{BT} = 4 \cdot \pi \times 0,256 \times 0,432 = 1,38{\rm{ m}}^2$

Considerando un coefficiente di trasmissione globale avvolgimento.olio pari a $K_T= 80 \frac {\rm{W}}{\rm{m}^2 \rm{K}}$ (vedi l'articolo sovrariscaldamento [11]), si ha

$\Delta \vartheta = \frac{{\frac{1}{3} \cdot P_{Cu,BT} }}{{K_T \cdot S_{D,BT} }} = \frac{{1041}}{{80 \times 1,38}} = 9,4 \, {\rm{ K}}$

Tenendo presente che è ammessa normativamente una sovratemperatura Rame-Olio di 15 K, la nostra è una macchina fredda. Si può pensare di rinunciare al canale intermedio di raffreddamento. Però in tal modo la superficie disperdente dimezza e la sovratemperatura raddoppia, diventando quasi 19 K. Per portarla a 15 K occorre diminuire le perdite nel rame aumentando la sezione, quindi diminuendo la densità di corrente.

La densità di corrente è inversamente proporzionale al peso

$\delta {\rm{ = }}\frac{{I_n }}{{S_{Cu,BT} }} = \frac{{I_n \cdot l}}{{S_{Cu,BT} \cdot V_{2,Cu} }} \to \partial \propto \frac{1}{{peso_{Cu}}}$

mentre le perdite sono direttamente proporzionali al peso ed al quadrato della densità, quindi complessivamente inversamente proporzionali al peso

$P_{Cu,BT} \propto peso_{Cu} \cdot \delta ^2 = \frac{1}{{peso_{Cu} }}$

Per avere una sovratemperatura massima di 15 K le perdite devono essere, senza il canale intermedio di raffreddamento, pari a

$P_{Cu,BT} = \Delta \vartheta _{\max } \cdot \frac{{S_{D,BT} }}{2} = 15 \times 0,69 \times 80 = 828{\rm{ W}}$

quindi diminuire del $\frac{{{\rm{1041 - 828}}}}{{1040}} \times 100 \approx 21 \%$ , quindi il peso di rame aumenterà nella stessa percentuale.

$P_{Cu}=48,2 \times 1,21 \approx 58 \, {\rm{kg}}$

Il volume è proporzionale alla sezione di rame, che aumenta dunque del 21% diventando

$S_{Cu,BT} = 306 \times 1,21 = 370{\rm{ mm}}^2$

Lasciando inalterata l'altezza di 36 mm, avremo una larghezza di 370/36 mm che arrotonderemo a 11 mm.

Con una piattina $5,5 \times 8,5$ la sezione di rame è

$S_{Cu,BT}=5,5 \times 8,5 \times 8=374 \, \text{mm}^2$

e la configurazione dell'avvolgimento senza canale intermedio tra gli strati è:

Sezione spira BT

In totale lo spessore del rame aumenta di 4 mm; è stato però eliminato il canale intermedio di raffreddamento di 6 mm. Lo spessore complessivo è allora ridotto di 2 mm. Il diametro esterno dell'avvolgimento risulta pertanto diminuito di 4 mm. Quindi

$D_{ext,BT}=278 \, {\rm{mm}}$

Il nuovo diametro medio è allora di $D_{medio,BT}= 254 \, {\rm{mm}}$

Ricapitolando, con le nuove dimensioni:

$\delta=\frac {910}{374}=2,43 \, \frac {\rm{A}}{\rm{mm}^2}$

$\begin{array}{l} P_{Cu} = \pi \cdot D_{medio,BT} \cdot S_{Cu,BT} \cdot N_2 \cdot p_{Cu} = \\ = \pi \times 0,254 \times 374 \times 10^{ - 6} \times 22 \times 8900 = 58,4{\rm{ kg}} \\ \end{array}$

$P_{Cu,BT}=3 \times 2,4 \times 58,4 \times 2,43^2 =2483 \, {\rm{W}}$

$\Delta \vartheta = \frac{{\frac{1}{3} \cdot P_{Cu,BT} }}{{K_T \cdot S_{D,BT} }} = \frac{{828}}{{80 \times \frac {1,38}{2}}} = 15{\rm{ K}}$

Avvolgimento A.T.

Manteniamo l'altezza identica a quella dell'avvolgimento B.T. : $h_{AT}=h_{BT}=430 \, \text{mm}$

L'olio serve, oltre che per il raffreddamento, per l'isolamento. La sua rigidità dielettrica di lavoro è

$K_{c,olio}=50 \frac {\rm{kV}}{cm}$

La tensione da considerare per l'isolamento AT/BT è il picco della tensione di prova prevista che, nel nostro caso è $U_P=28 \, \text {kV}$ , quindi:

$U_{p,max}=\sqrt{2} \cdot U_p=\sqrt {2} \times 28 \approx 40 \, \rm{kV}$

Tra i due avvolgimenti occorre un canale d'olio di larghezza

$s_{co}=\frac {40}{50}=0,8 \, \rm{cm}$

Inseriamo anche un cartoccio di $s_c=3 \, \text{mm}$ di spessore, che ha una rigidità di circa $100 \, \frac {\text{kV}}{\text{cm}}$ che quindi, già da solo, regge quasi la tensione di prova.

Dobbiamo pure prevedere anelli di supporto e di isolamento. Usiamo cartone che regge 1 kV di prova per ogni millimetro. Gli anelli avranno uno spessore di 28 mm che arrotondiamo a tre centimetri.

L'altezza della colonna su cui saranno infilati gli avvolgimenti dovrà essere almeno $h_c=h_{AT}+2 \cdot s_c=430+2 \times 30=490 \, \text{mm}$ . Per una maggior sicurezza costruttiva considereremo $h_{colonna}=500 \, \text{mm}$

Il numero di spire sarà

$N_1=\frac {U_{1n}}{E_s}=\frac {10.500}{10,5}=1000$ cui devono essere aggiunte $n_{reg}=\frac {0,05 \cdot U_{1n}} {E_s}=\frac {525}{10,5}=50$ spire di regolazione

La corrente che le percorre è ricavabile dalla

$I_1=I_2 \cdot \frac {N_2}{N_1}=910 \times \frac {22}{1000}=20 \, \text{A}$

Fissando una densità $\delta=3,5 \frac {\text{A}}{\text{mm}^2}$ , occorre una sezione di $S_{AT}=5,7 \, \text{mm}^2$ . Va bene un filo di diametro $d=2,7 \, \text{mm}$ . Il filo deve essere isolato. Useremo 5 carte di spessore 0,1 mm per cui il diametro d'ingombro del filo sarà di $d_f=3,2 \, \text{mm}$ .

Sezione AT: dimensioni in mm

Uno strato di avvolgimento sarà allora composto da $N_{sp/strato}=\frac {h_{col}}{d_f}=\frac{430}{3,2}=133$ spire. Per completare l'avvolgimento occorrono $n_s=\frac {N1}{N_{sp/strato}}=\frac{1050}{133}=8$ strati. Osserviamo però che tra strato e strato

Tensione tra due strati

si presenta una tensione di $V_{ss}=133 \cdot 2 \times 10,5=2793 \, \text {V}$ che sono troppi: al massimo ammettiamo 2500 V. Suddividiamo allora l'avvolgimento in due bobine che saranno collegate in serie. Una bobina sarà composta di $\frac {1050}{2}=525$ spire che suddivideremo in 8 strati di 60 spire più uno da 45. La tensione massima tra strato e strato diventa $120 \times 10,5=1260 \text{V}$ . Separiamo poi ogni strato con due millimetri di carta. Inoltre suddividiamo gli strati in due gruppi separati con cartone ondulato di spessore $5mm$ .

Spessore AT

Possiamo ora calcolare lo spessore dell'avvolgimento:

$s_{AT}=9 \times 32 +8 \times 0,2 + 5 = 35 \text{mm}$

L'altezza di ogni bobina è $h_b=3,2 \times 60 =192 \to 195 \, \text{mm}$

Tra una bobina e l'altra sarà posto un anello di cartone di $40mm$ di spessore

Il diametro interno dell'avvolgimento, tenendo conto del cartoccio di 3 mm tra avvolgimento di alta e quello di bassa, e di due canali d'olio da 6 mm per la circolazione dell'olio, è

$D_{int,AT}=280+(3+6+6) \times 2=310 \, \text{mm}$

mentre il diametro esterno vale

$D_{ext,AT}=D_{int,AT}+2 \cdot s_{AT}=310+2 \times 35= 380 \, \text{mm}$

Perdite e sovratemperatura

Il peso in rame dell'avvolgimento

$P_{Cu,AT}=\pi \cdot D_{m,AT} \cdot S_{AT} \cdot N_1 \cdot p_{Cu}=$ = $\pi \cdot 3,45 \times 5,7 \times 10^{-4} \times 1000 \times 8,9=55 \, \text{kg}$

In base all [1] del paragrafo perdite e sovratemperatura, calcoliamo le perdite totali nominali dell'avvolgimento AT

$P_{Cu,AT}=3 \times 2,4 \times 55 \times (3,5)^2 =4851 \, \text{W}$

La superficie disperdente è, tenendo conto di un coefficiente di riduzione di 0,5 per le due superfici cilindriche affacciate dei due gruppi di 4 e 4+1 strati

$\begin{array}{l} S_{D,AT} = 2 \cdot h_{s,AT} \cdot \pi \cdot \left( D_{int,AT} + D_{ext,AT} + 2D_{m,AT} \cdot 0,5 \right) \\ S_{D,AT} = 2 \times 0,195 \times \pi \times \left( 0,31 + 0,38 + 0,345 \right) = 1,27 \, {\rm{ m}}^2 \approx 1,3{\rm{ m}}^2 \\ \end{array}$

Per cui la sovratemperatura rispetto all'olio è

$\Delta \theta_{AT}=\frac {\frac {P_{AT}}{3}}{S_{D,AT} \cdot K_T}=\frac {1617}{1,27 \times 80}=16 \, K$

accettabile.

Il circuito magnetico

La sezione del nucleo è a gradini. La massima larghezza della sezione è di 200 mm; il diametro del cerchio circoscritto di 210 mm. La distanza tra gli assi delle colonne è di 410 mm, lasciando un canale di 30 mm tra gli avvolgimenti AT di due colonne adiacenti (190x2+30=410).

Trasformatore 630 kVA - quote in cm

Perdite nel Ferro

Il peso del circuito magnetico, essendo $p_{specifico,Fe}=7,7 \, \frac {\text {kg}}{\text{dm}^3}$ è dato da

$Peso_{colonna} = S_{Fe} \cdot h_{colonna} \cdot p_{specifico,Fe} = 2,8 \times 5 \times 7,7 = 108 \, {\rm{ kg}}$ $Peso_{giogo} = S_{Fe} \cdot L_{giogo} \cdot p_{specifico,Fe} = 2,8 \times 10,2 \times 7,7 = 220 \, {\rm{ kg}}$ $Peso_{Fe} = 3 \cdot Peso_{colonna} + 2 \cdot Peso_{gioghi} = 3 \times 108 + 2 \times 220 = 764 \, \text{kg}$

Le perdite nel Ferro le stimiamo maggiorando del 50% le perdite teoriche ricavabili con la cifra di perdita

$P_{Fe,teoriche} = C \cdot B_M^2 \cdot Peso_{Fe} = 0,5 \times 1,7^2 \times 764 = 1104{\rm{ W}}$ $P_{Fe}=1,5 \cdot P_{Fe,teoriche} =1,5 \times 1104 =1656{\rm{ W}}$

Nota: la cifra di perdita è riferita ad all'induzione di 1 T e le perdite dipendono dal quadrato dell'induzione massima.

Corrente a vuoto

La corrente a vuoto si ricava con

$I_0 = \sqrt {I_{_\mu }^2 + I_{_a }^2 }$

Per la stima del valore efficace della corrente magnetizzante $I μ$ , si considera un percorso costituito da una colonna, un interasse e due traferri. Un "buon" traferro con giunti affacciati è, di solito, $t=0,05 \, \text {mm}$ .

Nei lamierini usati, all'induzione di $B_M=1,7 \, \text{T}$ corrisponde un campo $H=200 \, \frac {\text{A}}{\text{m}}$ .

La tensione magnetica necessaria per stabilire il flusso nel percorso interasse giogo-colonna è $\Im _{Fe} = H \cdot \left( {l_{{\rm{interasse}}} + h_{col} } \right) = 2 \times \left( {41 + 50} \right) = 182 \, {\rm{ A}}$

Quella necessaria per il traferro è invece

$\Im _{\rm{t}} = H_t \cdot 2t = \frac{{B_M }}{{\mu _0 }} \cdot 2t = \frac{{1,7}}{{1,256}} \times 10^6 \times 2 \times 0,05 \times 10^{ - 3} = 135{\rm{ A}}$

Quindi

$I_\mu = \frac{{\Im _{Fe} + \Im _{\rm{t}} }}{{N_1 \cdot \sqrt 2 }} = \frac{{317}}{{1000 \times \sqrt 2 }} = 0,224{\rm{ A}}$

La componente attiva $I a$ si ricava dalle perdite nel ferro $I_a = \frac{{\frac{{P_{Fe} }}{3}}}{{U_1 }} = \frac{{552}}{{10500}} = 0,052{\rm{ A}}$

Dunque

$I_0 = \sqrt {0,224^2 + 0,052^2 } \approx 0,23{\rm{ A}}$

Rendimento

Valutiamo il rendimento a pieno carico con fattore di potenza unitario. Maggioriamo le perdite nel rame e nel ferro calcolate del 10%; otteniamo $P_{tot} = 1,1 \cdot \left( {P_{Fe} + P_{Cu,AT} +P_{Cu,BT}} \right) = 1,1 \times \left( {1656 + 4869 + 2842} \right) = 10303{\rm{ W}}$

$\eta = \frac{{630}}{{630 + P_{tot} }} \approx \frac{{630}}{{{\rm{640}}}} = 0,984$

Circuito equivalente di una fase

La reattanza longitudinale equivalente di una fase del primario si può stimare con la formula $X_{1c} = 8,4\frac{{N_1^2 }}{h} \cdot f \cdot \pi \cdot D_{m,ATBT} \cdot \left( {d + \frac{{s_{AT} + s_{BT} }}{3}} \right) \cdot 10^{ - 8} \, {\rm{ }}\Omega$

dove $d = D i n t, A T - D e x t, B T$ è la distanza che separa gli avvolgimenti AT e BT; $D_{m,ATBT}=\frac {D_{int, AT}+D_{ext, BT}}{2}=29,5 \, \text{cm}$ , è il diametro medio degli avvolgimenti; $h=43 \, \text{cm}$ è l'altezza degli avvolgimenti; f la frequenza di alimentazione; $N 1$ il numero di spire nominali del primario. Quindi si ha

$X_{1c} = 8,4\frac{{10^{ - 2} }}{{43}} \times 50 \times \pi \times 29,5 \times \left( {1,5 + \frac{{3,5 + 2,5}}{3}} \right) = 32 \, {\rm{ }}\Omega$

La resistenza longitudinale si ricava dalla perdite nel rame

$R_{1c} = \frac{{\frac{{P_{Cu} }}{3}}}{{I_1^2 }} = \frac{{\frac{{4869 + 2580}}{3}}}{{400}} = 6,2 \, {\rm{ }}\Omega$

La resistenza trasversale si ricava dalle perdite a vuoto, quindi dalla componente attiva della corrente a vuoto

$R_0 = \frac{{U_1 }}{{I_a }} = \frac{{10500}}{{0,052}} \approx 202{\rm{ k}}\Omega$

La reattanza trasversale dalla corrente magnetizzante

$X_0 = \frac{{U_1 }}{{I_\mu }} = \frac{{10500}}{{0,224}} \approx 47{\rm{ k}}\Omega$

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Dimensionamento del cassone

Il cassone deve dissipare il calore sviluppato in modo che l'olio assuma temperature eccessive. La sovratemperatura massima dell'olio rispetto all'aria deve essere di 60 K. Noi considereremo una sovratemperatura media di di 50 K come limite.

Il cassone disperde il calore verso l'ambiente per convezione e per irradiazione.

Per entrambe si può assumere in prima approssimazione una legge che stabilisce la potenza termica dispersa proporzionale alla differenza di temperatura tra olio ed aria, come mostrato nell'articolo Sovrariscaldamento(formula [11]; [8] per la convezione naturale.

Se immaginiamo un cassone liscio di $132 \times 50 \times 1300 \, \text{cm}^3$ , considerando come disperdente la superficie laterale

$S_d=p_{cass} \cdot h_{cass}=2 \times (1,32 + 0,5 ) \times 1,3 =3,64 \times 1,3=4,73 \text {m}^2$ considerando

$K_i=6 \, \frac {\text{W}}{\text{m}^2 \, \text{K}}$ , per l'irradiazione,

$K_c=6,5 \, \frac {\text{W}}{\text{m}^2 \, \text{K}}$ , per la convezione

$\Delta \theta=50 \, \text{K}$ salto di temperatura tra olio-cassone ed aria

abbiamo una

$P_{dc}=\left (K_i+K_c \right ) \cdot S_d \cdot \Delta \theta=12,6 \times 4,73 \times 50=$

$= 1419_{irr} + 1561_{conv}=2980 \, \text {W}$

La potenza da dissipare è però di circa $10.000 \, \text{W}$

Occorre dunque aumentare la superficie disperdente. Lo possiamo fare usando due file di tubi. La sezione dei tubi disponibili è la seguente

Sezione Tubo.gif

Il cui perimetro è

$p_{Sez,tubo}=2 \times (40+ \pi \times 20)=143 \, \text {mm}$

Cassone del Trasformatore 630 kVA

La prima fila esterna è lunga

$L_{tubo,ext}=90 + 2 \times 25= 140 \, \text{cm}$

quella interna

$L_{tubo,int}=70 + 2 \times 11= 92 \, \text{cm}$

La superficie laterale dei tue tubi

$S_{L,coppia}=(L_{tubo,ext}+L_{tubo,int}) \cdot p_{Sez,tubo} =2,32 \times 0,143=0,33 \, \text {m}^2$

Con i tubi aumenta anche la superficie irradiante che è uguale al perimetro del poligono tangente al bordo dei tubi esterni per l'altezza del cassone, quindi

$S_{irr1}=h_{cass} \cdot p_{tubi}=1,3 \times (2 \times (1,32 + 0,5 )+4 \times 0,28 \sqrt{2})=6,8 \, \text{m}^2$

quindi aumenta la potenza irradiata

$P_{irr1}=6 \times 6,8 \times 50=2040 \, \text{W}$

Rimane da dissipare per convezione

$P_{c,tubi}=P_p -P_{irr1}-P_{conv}=10000-2040-1561 \approx 6400 \, \text{W}$

Occorre dunque che sviluppino una superficie

$S_{tubi}=\frac {P_{c,tubi}}{K_c \cdot \Delta \theta}=\frac {6400}{6,6 \times 50}=19,4 \, \text{m}^2$

Sono necessari almeno

$n_{coppie,tubi}= \frac {S_{tubi}}{S_{L,coppia}}=\frac{19,4}{0,33} \approx 60$

Il passo tra le coppie delle due file di tubi è

$p_t=\frac {p_{cass}}{n_{coppie,tubi}}=\frac {364}{60} \approx 6 \, \text{cm}$

Bibliografia

Costruzioni Elettromeccaniche - Giovanni Someda Ed. Patron
Appunti di lezione del prof. Luciano Merigliano, 1972
http://www-3.unipv.it/dmae/materiale_didattico/Costruzioni_1_Materiali_magnetici.pdf
Elettrotecnica Applicata -Bressi-Corticelli-Cremonini-Zerbetto Ed. Zanichelli
Quaderno Tecnico Schneider su Prove di Collaudo dei Trasformatori

ElectroYou - la comunità dei professionisti del mondo elettrico

Progetto di un trasformatore di potenza MT/BT

Indice

Sintesi del procedimento

Dati

Dimensionamento preliminare

Avvolgimento B.T.

Perdite e sovratemperatura

Avvolgimento A.T.

Perdite e sovratemperatura

Il circuito magnetico

Perdite nel Ferro

Corrente a vuoto

Rendimento

Circuito equivalente di una fase

Dimensionamento del cassone

Bibliografia

Inserisci un commento

Argomenti correlati

Tag Cloud

Informazioni

Seguici

Pubblicità

Credits