Indice |
Ci eravamo lasciati...
...qui.
L'effetto fotoelettrico
La figura schematica di sopra mostra un apparecchio usato per lo studio dell'effetto fotoelettrico.
Un fascio di luce monocromatica, che incide su una lastra di metallo A, libera dei fotoelettroni, che possono essere rivelati sotto forma di corrente qualora vengano attratti dalla cavità metallica B per mezzo di una differenza di potenziale V applicata tra A e B.
Il galvanometro G consente di misurare questa corrente fotoelettrica.
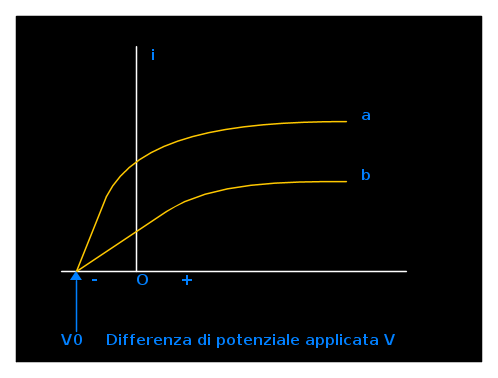
Consideriamo ora la seguente figura:
essa (curva a) rappresenta il grafico della corrente fotoelettrica in un apparecchio simile a quello schematizzato sopra, in funzione della differenza di potenziale V. Se V è abbastanza grande la corrente fotoelettrica arriva fino ad un certo valore limite ed in corrispondenza di tale valore tutti i fotoelettroni che sono emessi dalla lastra A sono raccolti dalla cavità B.
Cambiando il segno di V, la corrente fotoelettrica non scende subito a zero: ciò dimostra il fatto che gli elettroni sono emessi da A ad una velocità finita; alcuni di essi raggiungeranno la cavità B nonostante il campo elettrico si opponga al loro moto. Però se questa differenza di potenziale, cambiata di segno, viene resa sufficientemente grande, si raggiunge un valore detto potenziale critico, indicato con V0, in corrispondenza del quale la corrente fotoelettrica si riduce a zero. Tale differenza di potenziale V0, moltiplicata per la carica dell'elettrone, misura l'energia cinetica Kmax del fotoelettrone emesso più veloce. In sostanza si ha:

Kmax è indipendente dalla velocità della luce, come indicato dalla curva b della figura di cui sopra, in cui l'intensità luminosa è stata ridotta della metà.
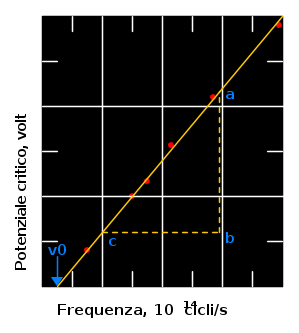
Nella figura che segue, invece, è riportato il potenziale critico V0 in funzione della frequeza della luce incidente, per il sodio:
Si vede che vi è una precisa frequenza di taglio ν0, al di sotto della quale non si verifica l'effetto fotoelettrico.
Questi dati furono raccolti da Millikan a cui nel 1923 fu assegnato il premio Nobel per i suoi risultati sull'effetto fotoelettrico.
Dato che l'effetto fotoelettrico interessa in particolare la superficie del metallo è importante evitare pellicole di ossido, di grasso e più in generale altre contaminazioni superficiali.
Millikan elaborò una tecnica per tagliare, sotto vuoto, delle lamine sottili, dalla superficie metallica, costruendosi, una sorta di "officina del vuoto", come lui la definiva.
Tre tra le più importanti caratteristiche dell'effetto fotoelettrico non sono spiegabili con la teoria ondulatoria della luce:
- La teoria ondulatoria della luce afferma che l'energia cinetica dei fotoelettroni aumenta con l'aumentare dell'intensità del fascio luminoso. Tuttavia, precedentemente, si è visto che Kmax è indipendente dall'intensità luminosa; ciò è stato verificato per un intervallo di intensità di 107.
- Secondo la teoria ondulatoria della luce l'effetto fotoelettrico si dovrebbe verificare per una qualsiasi frequenza della luce, a patto che questa sia abbastanza intensa. Si è visto però che esiste, per ciascuna superficie, una frequenza di taglio caratteristica ν0. Per frequenze inferiori a questa l'effetto fotoelettrico scompare, qualunque sia l'intensità dell'illuminazione.
- Se l'energia dei fotoelettroni è quella ceduta dall'onda incidente alla lamina di metallo, è improbabile che l'area dalla quale l'elettrone nel metallo può assorbire energia sia molto superiore a quella corrispondente ad alcuni diametri atomici. In questo modo, se l'intensità luminosa è molto piccola, dovrebbe esserci un ritardo di tempo misurabile tra l'arrivo della luce sulla superficie e l'emissione del fotoelettrone. Durante questo intervallo di tempo l'elettrone dovrebbe assorbire energia dal fascio fino a quando non ne ha accumulata abbastanza per uscire dal metallo.
Invece non è stato mai misurato alcun ritardo.
Questo disaccordo è sorprendente quando la sostanza sulla quale si verifica l'effetto fotoelettrico è un gas: infatti in questo caso l'energia del fotoelettrone emesso deve essere trasferita dal fascio ad un singolo atomo.
Einstein e la teoria del fotone
Einstein riuscì a spiegare l'effetto fotoelettrico ed avanzò in tal senso una ipotesi notevole: l'energia in un fascio luminoso viaggia nello spazio divisa in pacchetti, detti fotoni.
L'energia E di un fotone è esprimibile mediante la seguente relazione:

Planck pensava che la luce, nonostante fosse emessa dalla sorgente in modo discontinuo, si propagasse nello spazio sotto forma di onda elettromagnetica.
L'ipotesi di Einstein afferma che la luce, viaggiando nello spazio, non si comporti come un'onda ma come una particella.
Millikan, i cui esperimenti confermavano le ipotesi di Einstein, definì l'ipotesi stessa di einstein come "audace per non dire avventata".
Applicando il concetto di fotone all'effetto fotoelettrico, Einstein pervenne a:

dove hν è l'energia del fotone.
L'equazione scritta sopra afferma quindi che un fotone introduce nella superficie un'energia hν e parte di tale energia (E0) permette di far passare l'elettrone attraverso la superficie metallica.
L'energia che resta (hν − E0) è ceduta all'elettrone in forma di energia cinetica. Se l'elettrone non perde energia a causa di collisioni interne mentre esce dal metallo, conserverà tale energia come energia cinetica. In questo modo Kmax è l'energia cinetica massima che il fotoelettrone può avere fuori dalla superficie; in quasi tutti i casi esso sarà dotato di un'energia minore per via delle perdite interne.
Consideriamo come l'ipotesi del fotone di Einstein risponda alle tre "obiezioni" che sono state sollevate contro l'interpretazione dell'effetto fotoelettrico tramite la teoria ondulatoria della luce.
Per quanto riguarda la prima obiezione (indipendenza di Kmax dall'intensità di illuminazione), c'è un accordo completo tra la teoria del fotone e l'esperimento.
Se si raddoppia l'intensità luminosa si raddoppia semplicemente il numero dei fotoni e quindi la corrente fotoelettrica, mentre non cambia l'energia ( = hν) dei singoli fotoni.
La seconda obiezione viene aggirata ricorrendo ancora all'equazione (1) scritta sopra.
Infatti se Kmax è pari a zero, si ha:

che afferma che il fotone ha un'energia appena sufficiente ad estrarre i fotoelettroni e nessuna in sovrappiù da comunicare come energia cinetica. Questa quantità E0 è chiamata lavoro di estrazione della sostanza.
Se ν è inferiore a ν0 i singoli fotoni, indipendentemente dal loro numero, non avranno energia sufficiente ad estrarre fotoelettroni.
La terza obiezione è rimossa dalla teoria del fotone, perché l'energia che richiesta è fornita in quantità discreta e non distribuita uniformemente su una vasta area, come nella teoria ondulatoria.
Nonostante l'ipotesi del fotone spieghi i fenomeni della fotoelettricità, essa sembra essere in conflitto con la teoria ondulatoria della luce che permette di interpretare correttamente moltissimi esperimenti.
Il moderno punto di vista riguardo la natura della luce è che essa abbia un carattere duale poiché si comporta come un'onda in certe circostanze e come una particella, o fotone, in altre.
Riscriviamo ora l'equazione (1) dell'effetto fotoelettrico di Einstein, sostituendo eV0 a Kmax :

La teoria di Einstein prevede una dipendenza lineare tra V0 e ν, in accordo con l'esperienza.
La pendenza della curva sperimentale riportata nella figura 1 dovrebbe essere h / e, cioè:

Possiamo ricavare h moltiplicando questo rapporto per la carica dell'elettrone e:

Da una analisi più precisa di questo dato e di altri dati, compresi quelli relativi alla superficie di litio, Millikan trovò il valore  , con un errore dello 0,5 % circa.
, con un errore dello 0,5 % circa.
Questo accordo con il valore di h ricavato dalla formula della radiazione di Planck è una conferma del concetto di fotone di Einstein.
L'effetto Compton
Una conferma definitiva del concetto di fotone come quanto di energia fu data nel 1923 da A. H. Compton che ottene per il suo lavoro il Nobel nel 1927.
Compton inviò un fascio monocromatico di raggi X di lunghezza d'onda λ su un blocco di grafite, come schematizzato nella figura che segue e misurò, per diversi angoli di diffusione, l'intensità dei raggi X in funzione della lunghezza d'onda:
La figura che segue, invece, mostra i risultati dell'esperimento condotto.
Si vede che per quanto il fascio incidente abbia una sola lunghezza d'onda λ, i raggi X diffusi hanno dei picchi di intensità a due lunghezze d'onda; uno di essi corrisponde alla lunghezza d'onda incidente e l'altro alla lunghezza d'onda λ' più grande della precedente di Δλ, che è denominato spostamento Compton, il quale varia con il variare dell'angolo a cui i raggi X diffusi sono osservati.
La presenza di un'onda diffusa di lunghezza d'onda pari a λ' non può essere spiegata se si considera i raggi X incidenti come un'onda elettromagnetica secondo una descrizione in cui l'onda incidente, di frequenza ν, fa sì che gli elettroni del blocco sul quale si ha la diffusione, oscillino alla stessa frequenza. Questi elettroni che oscillano si possono paragonare alle cariche che si muovono avanti e indietro in una antenna radio piccolissima ed irradiano onde elettromagnetiche della medesima frequenza ν. Quindi nella descrizione ondulatoria l'onda diffusa dovrebbe avere la stessa frequenza e lunghezza d'onda dell'onda incidente.
Compton riuscì a spigare i risultati dei suoi esperimenti arrivando a postulare che il fascio di raggi X incidente non è un'onda, bensì un insieme di fotoni di energia E pari a hν e che questi urtano gli elettroni liberi nel blocco su cui avviene la diffusione.
I fotoni "di rinculo" che escono dal blocco, da questo punto di vista, costituiscono la radiazione diffusa.
Poiché il fotone incidente trasferisce un po' della sua energia all'elettrone con cui entra in collisione, il fotone diffuso deve possedere una energia inferiore E'; dovrà quindi avere una frequenza inferiore ν' (pari ad E' / h) e quindi si avrà una lunghezza d'onda più elevata pari a λ' (cioè a c / ν').
Tale descrizione considera tiene conto dal punto di vista qualitativo dello spostamento di lunghezza d'onda Δλ.
Questo modello a particelle della diffusione dei raggi X è diverso da quello che si basa sulla descrizione ondulatoria.
Analizziamo ora dal punto di vista quantitativo la singola collisione tra fotone ed elettrone.
La seguente figura ritrae schematicamente la collisione tra il fotone e l'elettrone.
si ipotizza che l'elettrone sia a riposo e libero, cioè non legato agli atomi del diffusore.
Applichiamo alla collisione la legge della conservazione dell'energia. Poiché gli elettroni di rinculo possono avere una velocità v paragonabile a quella della luce occorre adoperare l'espressione relativistica dell'energia cinetica dell'elettrone.
Possiamo quindi scrivere:

in cui il secondo termine del secondo membro rappresenta l'espressione relativistica dell'energia cinetica dell'elettrone di rinculo, dove m è la massa relativistica ed m0 è la massa a riposo dell'elettrone.
Sostutuiamo e / λ a ν ed adoperando opportune sostituzioni per eliminare la massa relativistica m si ottiene:

Applichiamo ora la legge vettoriale di conservazione della quantità di moto alla collisione della figura 2.
Occorre innanzitutto tenere conto l'espressione dell'impulso del fotone.
Se un oggetto assorbe totalmente un'energia U da un fascio parallelo di luce che incide su di esso, il fascio luminoso, secondo la teoria ondulatoria della luce, trasferisce in maniera simultanea all'oggetto un impulso dato da U / c.
Nella descrizione a fotoni immaginiamo che questo impulso venga trasportato dai singoli fotoni, ognuno dei quali trasporta impulso in quantità p = hν / c, dove h è l'energia del fotone.
Sostituendo quindi λ a c / ν si ha:

L'espressione relativistica della quantità di moto dell'elettrone è data dalla seguente relazione:

Per la conservazione della componente x della quantità di moto si può scrivere:

e per la componente y si può scrivere:

Ora dobbiamo trovare la variazione di lunghezza d'onda, in modo tale da poterla confrontare con i risultati sperimentali della figura 2.
Nell'esperimento di Compton non fu esaminato l'elettrone di rinculo. E' possibile eliminare due dei cinque parametri (λ,λ',ν, ,θ) che compaiono nelle equazioni finora scritte.
,θ) che compaiono nelle equazioni finora scritte.
Eliminiamo ν e θ che riguardano solo l'elettrone e così si perviene ad un'unica relazione tra i parametri; effettuando gli opportuni procedimenti algebrici si arriva a:

In questo modo lo spostamento Compton Δλ dipende solo dall'angolo di diffusione  e non dalla lunghezza d'onda iniziale λ.
e non dalla lunghezza d'onda iniziale λ.
L'ultima equazione scritta prevede entro gli errori gli spostamenti Compton della figura 2 osservati sperimentalmente.
Si nota inoltre che Δλ varia da 0 a 2h / m0c.
Dobbiamo spiegare ora la presenza del picco della figura 2 per cui in lunghezza d'onda non varia nella diffusione. Questo picco si può spiegare come risultante da una collisione tra fotoni ed elettroni legati a ioni del blocco su cui avviene la diffusione.
Nelle collisioni gli elettroni legati si comportano come gli elettroni liberi considerati nell'ultima equazione scritta, con la differenza che la loro massa efficace è molto più grande. Ciò è dovuto al fatto che nella collisione rincula tutto il complesso ionico.
La massa efficace M per un diffusore di carbonio è circa pari alla massa di un nucleo di carbonio.
Si avrà approssimativamente  .
.
Sostituendo M ad m0 nell'ultima equazione scritta si ha che lo spostamento di Compton per collisioni con elettroni strettamente legati è così piccola da non potersi misurare.
Bibliografia
Fisica 2. Elettromagnetismo-ottica - David Halliday, Robert Resnick

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)