Indice |
Considerazioni iniziali
Consideriamo un filo di rame ed una batteria collegata alle sue estremità come in figura:
Si applica al filo una differenza di potenziale V che favorisce il passaggio di una corrente i. La legge di Ohm dice che il flusso di corrente i è esprimibile mediante la relazione che segue:

dove R è la resistenza del filo misurata in ohm, V è misurata in volt (V) e i in ampere (A).
Se prendiamo ora in considerazione R (cioè la resistenza del filo), l (cioè la sua lunghezza) ed A (cioè la sua sezione traversale), tali grandezze sono legate dalla relazione:

dove ρ è detta resistività elettrica e si misura in ohm-metro.
Introduciamo inoltre la seguente grandezza, detta conducibilità elettrica, che ci consente di fare delle valutazioni non dal punto di vista della resistenza bensì dal punto di vista del passaggio di corrente elettrica:

la cui unità di misura è l'inverso di quella della resistività, come si può intuire dalla relazione precedentemente scritta.
Di seguito i valori di conducibiità elettrica di alcuni metalli e non metalli:
| Metalli e leghe | conducibilità (Ω m)-1 | Non metalli | conducibilità (Ω m)-1 |
|---|---|---|---|
| Argento | 6,3 x 107 | Germanio | 2,2 |
| Oro | 4,2 x 107 | Silicio | 4,3 x 10-4 |
| Rame (purezza commerciale) | 5,8 x 107 | Diamante | 10-14 |
| Alluminio (purezza commerciale) | 3,4 x 107 | Polietilene | 10-14 |
In maniera intuitiva possiamo dire che, dipendentemente dalla conducibilità eletttrica più o meno bassa, si possono distringuere i materiali conduttori elettrici (come argento, oro, rame) con le conducibilità elettriche più alte (e in grado di "far scorrere al loro interno la corrente con facilità") dagli isolanti elettrici con conducibilità molto basse.
In tal senso hanno "proprietà intermedie" i semiconduttori. Essi hanno cioè valori di σ intermedi tra quelli dei conduttori e degli isolanti.
La legge di Ohm, però, esprimibile anche in un'altra forma, oltre a quella più comune i=V/R vista prima che è detta anche forma macroscopica della legge di Ohm. Tale seconda forma è detta, di contro, forma microscopica:

dove E e J sono rispettivamente il campo elettrico (V/m) e la densità di corrente (A/m2). Differentemente dalle grandezze viste sinora, E e J sono grandezze vettoriali.
Mancano ancora due concetti:
- velocità di deriva degli elettroni;
- resistività elettrica dei metalli.
Velocità di deriva degli elettroni
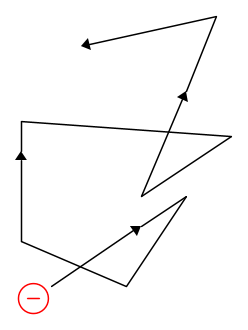
Il fisico tedesco Paul Drude agli inizi del 1900 propose un modello che spiegava la conduzione elettrica nei metalli. Tale modello fu poi sviluppato successivamente da Lorentz. Tale modello suppone che gli ioni del reticolo cristallino del conduttore metallico siano in una posizione fissa e che gli elettroni si muovano all'interno del reticolo cristallino secondo un moto disordinato, che interagiscano con gli ioni mediante urti. Tra un urto e il successivo la traiettorai mantenuta dall'elettrone è rettilinea, sicchè nelcomplesso il moto, peraltro casuale, dell'elettrone è "raffigurabile" mediante un insieme di linee spezzate, come in figura:
Non si ha una corrente in nessuna direzione. In altre parole non c'è un flusso netto di carica. Introduciamo quindi due grandezze:

dove τ è detto tempo medio e l (da non confondersi con la l prima citata in relazione alla legge di Ohm) è il cammino libero medio esistente tra due urti successivi v è la velocità degli elettroni nel metallo.
Quanto detto finora però presume una importante ipotesi di fondo: l'assenza di un campo elettrico E.
Qualora accada il contrario, cioè applicando un campo elettrico E, le cose cambiano e ogni elettrone acquista una accelerazione a=F/m uguale a -eE/m opposta al campo elettrico e non si hanno più delle spezzate, come prima, ma degli archi di parabola, più o meno come in figura:
Diventa necessario considerare ora una velocità vd altresì detta velocità di deriva che è piccola rispetto alle velocità dei singoli elettroni. Per questo motivo possiamo dire che il τ non cambia tra due urti consecutivi. Detta vi la velocità di un elettrone subito dopo un urto e vi+1 quella prima dell'urto successivo:

Possiamo operare una media su un gran numero di urti N e definire la velocità di deriva come:

Il primo termine della differenza è nullo in quanto la distribuzione delle velocità è casuale dopo ogni urto, quindi:

In pratica grazie al campo E applicato, ogni elettrone acquista una velocita vd nella direzione del campo stesso e proporzionale ad esso.
In definitiva, la densità di corrente J risulta:

Convenzionalmente però la corrente elettrica è ritenuta un flusso di carica positivo per cui :

n, lo ricordiamo, è il numero di elettroni per unità di volume.
Resisitività elettrica dei metalli
La resistività elettrica per un metallo puro può essere approssimativamente definita come:

La componente termica deriva dalle vibrazioni dei nuclei ionici attorno alle posizioni di equilibrio nel reticolo cristallino del metallo.
La componente residua è indipendente dalla temperatura e diventa rilevante solo a tamperature basse.
Per molti metalli, a temperature superiori ai -200°C la resistività elettrica varia in maniera quasi lineare con la temperatura e pertanto può essere approssimata in tale modo:

dove ρ0 è la resistività elettrica a 0°C, αT è il coefficiente di temperatura della resistività e T è la temperatura del metallo.
Esempio numerico
La conduttività del rame è  ;
;
la carica dell'elettrone  ;
;
il numero di elettroni per unità di volume nel rame vale  ;
;
Per una densità di corrente  , la velocità di deriva vale
, la velocità di deriva vale

I semiconduttori intrinseci
I semiconduttori intrinseci sono quei semiconduttori la cui conducibilità elettrica dipende dalle loro proprietà conduttive intrinseche. Esempi di semiconduttori intrinseci sono il germanio e il silicio.
Questi due elementi hanno la struttura cubica del diamante. La loro conducibilità elettrica può essere spiegata grazie a questa rappresentazione qualitativa:
In tale rappresentazione, i cerchi blu indicano i nuclei degli ioni positivi degli atomi di Silicio o Germanio, le doppie linee che li collegano sono gli elettroni di valenza di legame. Affinchè gli elettroniriescano amuoversi attraverso il reticolo cristallino e quindi a condurre l'elettricità, devono essere eccitati grazie a della energia che dovrà essere fornita che servirà per l'appunto a smuoverli dalle loro posizioni di legame. Così facendo l'elettrone diventa un elettrone libero di conduzione che lascia una lacuna con carica positiva all'interno del reticolo cristallino.
Diagramma delle bande di energia
L'utilizzo del diagramma delle bande di energia serve a descrivere l'eccitazione degli elettroni di valenza che diventeranno poi elettroni di conduzione. Tale rappresentazione tiene in considerazione solo l'energia richiesta per il processo e non descrive il movimento degli elettroni all'interno del reticolo.
Consideriamo dei semiconduttori intrinseci elementari come Silicio e Germanio. Il diagramma delle bande sarà del tipo in figura:
Gli elettroni di valenza del legame del cristallo occupano la banda di valenza più bassa, che risulta quasi piena alla temperatura di 20°C. Al di sopra della banda di valenza piena vi è un intervallo di energia, una differenza di energia, in cui non ci sono stati di energia possibili (per il Si si tratta di 1,1 eV a 20°C). Questo intervallo di energia si interpone più precisamente tra il livello più alto della banda di valenza e quello più basso della banda di conduzione.
Esso non è occupabile da elettroni. Viene definito intervallo di banda o band gap e rappresenta, in soldoni, l'energia che il singolo elettrone deve acquisire per poter "tranistare" dal livello più alto della banda di valenza a quello più basso della banda di conduzione.
L'energia termica a temperatura ambiente basta per l'eccitazione di alcuni elettroni dalla banda di valenza a quella di conduzione e, in questo modo, vengono a crearsi nella banda di valenza delle lacune elettroniche.
In definitiva i portatori di carica sono 2:
- lacuna di carica positiva;
- elettrone di carica negativa.
Dal punto di vista quantitativo
In tal caso la densità di corrente J è:

dove:
- n è il numero di elettroni di conduzione per unità di volume;
- p è il numero di lacune di conduzione per unità di volume;
- q è il valore assoluto della carica dell'elettrone e della lacuna;
- vn e vp sono le velocità di deriva di lacuna ed elettrone.
Tenendo conto che J=σE e dividendo tutto per E:

Le due quantità vn/E e vp/E sono dette mobilità dell'elettrone e della lacuna e sono un indice della velocità con cui si muovnon elettroni e lacune in un campo applicato.
Esse sono indicate anche con i simboli μn e μp; l'equazione precedente puà essere scritta nel modo più compatto che segue:

La mobilità si misura in m2/V s.
Volendo semplificare l'equazione si può fare la considerazione seguente: nei semiconduttori intrinseci elementari elettroni e lacune sono creati a coppie per cui il numero di elettroni di conduzione e di lacune di conduzione è identico:

dove n è la concentrazione intrinseca di elettroni e lacune, in pratica dei portatori di carica.
Si ottiene quindi:

Di seguito alcune proprietà del Silicio e Germanio a 300 K (fonte: da E.M.Conwell, "Properties of Silicon and Germanium II") :
| Proprietà | Silicio | Germanio |
|---|---|---|
| Intervallo di energia, eV | 1,1 | 0,67
|
| Mobilità dell'elettrone, m2/(V s) | 0,135 | 0,39
|
| Mobilità della lacuna, m2/(V s) | 0,048 | 0,19
|
| Densità dei portatori intrinseci ni, portatori/m3 | 1,5 x 1016 | 2,4 x 1019
|
Gli effetti della temperatura
Nei semiconduttori accade che all'aumentare della temperatura aumenta la conducibilità.
Ci ricordiamo che gli elettroni presenti nella banda di valenza piena sono attivabili termicamente. La loro concentrazione che prima abbiamo chiamato ni è in qualche modo dipendente dalla temperatura secondo la relazione:

dove nell'ordine:
- Eg è l'intervallo di energia;
- Eav è l'energia media di intervallo della banda;
- k è la costante di Boltzmann;
- T è la temperatura in K.
Per il Silicio e il Germanio Eav = Eg/2, per cui:

Cenni sul processo di drogaggio
Il silicio mostra delle interessanti proprietà dal punto di vista elettronico quando viene drogato.
Cosa vuol dire "drogare un semiconduttore"? Vuol dire che al Silicio puro, in questo caso preso come esempio (il drogaggio infatti è estendibile anche a tutti gli altri semiconduttori), vengono aggiunti altri elementi.
Ad esempio è possibile aggiungere al Silicio atomi del V gruppo della tavola periodica in modo tale che essi si sostituiscano ad atomi di Silicio nel reticolo.
In tal modo un atomo del genere ha cinque elettroni di valenza; ciascuno di questi atomi introduce all'interno del cristallo di Silicio un elettrone in più del necessario. Elementi del genere appartenenti al V gruppo (come l'arsenico) sono detti dononi in quanto donano un elettrone. Tali elettroni in più vanno ad occupare un livello di energia immediatamente al di sotto del livello più basso della banda di conduzione.
Viene da sè pensare, quindi, che questi elettroni avranno bisogno di poca, se non pochissima, energia per poter essere eccitati e passare alla banda di conduzione.
Uno dei metodi per drogare il silicio è la cosiddetta impiantazione ionica. In breve, si introducono ioni in un solido al fine di modificarne le proprietà fisiche utilizzando l'impiantatore ionico.
Un altro è rappresentato dalla diffusione termica, in cui il Silicio è portato a temperatura sufficientemente elevate al fine di consentire la diffusione del drogante nel silicio stesso. Il processo di drogaggio termina quando si estrae dal forno apposito il Silicio.
Ad onor del vero, per essere più precisi si parla di drogaggio dei wafer di Silicio, che sono sottili "fette" di materiale semiconduttore utilizzati per la realizzazione di circuiti integrati.
Quest'ultimo metodo, quello della diffusione termica, consiste in pratica nel portare la superficie del Silicio a temperature superiori ai 1100 °C in un forno costituito da un tubo di quarzo. Le parti della superficie di Silicio che non devono essere drogate sono mascherate in modo da poter lasciare "scoperte" solo le parti desiderate.
Bibliografia
- "Scienza e tecnologia dei materiali" - Hashemi, Smith;
- "Elementi di fisica - elettromagnetismo - onde" - Mazzoldi, Nigro, Voci.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)