Indice |
Le sorgenti luminose
Le sorgenti di luce più comuni sono i solidi incandescenti e i gas eccitati tramite una scarica elettrica.
Il filamento di tungsteno delle lampadine ad incandescenza e le comuni insegne al neon ne sono un esempio, come quelle che sono rispettivamente ritratte nelle figure sottostanti.
Se si analizza con uno spettrometro ottico la luce emessa da una sorgente si può conoscere l'intensità relativa alle varie lunghezze d'onda.
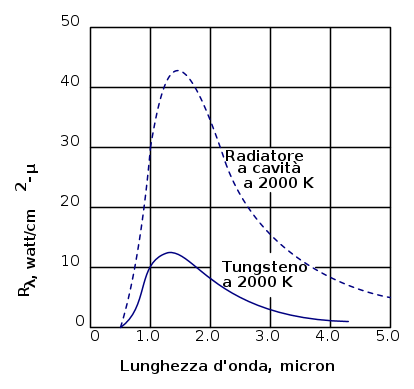
La figura che segue è tipica degli spettri dei solidi riscaldati e mostra i risultati di tali misure nel caso di un nastro di tungsteno scaldato alla temperatura di

(N.B.: il colore blu delle curve non è indicativo di alcunché) :
L'ordinata Rλ è detta irradianza spettrale (se ci si riferisce ad una sorgente è più corretto parlare di potere emissivo radiante o emittenza radiante) ed è definita in modo che la quantità Rλdλ sia l'energia irradiata nell'unità di tempo per unità di area della superficie, nell'intervallo di lunghezza d'onda compreso tra λ e λ + dλ. L'irradianza spettrale è espressa in W / m3. Nel misurare l'irradianza spettrale è inclusa tutta la radiazione emessa nell'emisfero anteriore.
Quando si vuole trattare l'energia irradiata senza però tenere conto della sua lunghezza d'onda si ricorre alla radianza che è l'energia irradiata per unità di superficie e di tempo nell'emisfero anteriore. Si misura in W / cm2 e può essere ricavata nel modo che segue:

cioè integrando la radiazione presente su tutti gli intervalli di lunghezze d'onda.
La radianza R può essere espressa come l'area sotto la curva che esprime Rλ in funzione di λ, visibile in Figura 1.
Per ogni materiale esiste una famiglia di curve di radianza simili a quelle della Figura 1, con una curva per ogni temperatura.
Confrontando queste famiglie di curve non si riscontrano regolarità evidenti e si presenterebbero difficoltà notevoli se si cercasse di comprenderle quantitativamente sulla base di una teoria fondamentale.
E' però possibile lavorare con un solido riscaldato idealizzato detto radiatore a cavità. Al variare della temperatura, le sue proprietà di emissione della luce sono rivelate in modo semplice e quindi il radiatore a cavità può essere definito come un solido ideale relativamente all'emissione della luce.
Le cavità radianti
Prendiamo ora in considerazione tre cavità realizzate all'interno di tre blocchi di metallo con un piccolo foro nella parete.
Assumeremo che i blocchi possano essere costituiti di un materiale qualsiasi, adatto però allo scopo, ovviamente, come il tungsteno, il tantalio e il molibdeno, tanto per fare un esempio.
Supponendo di condurre ad una stessa temperatura uniforme, misurata da un termometro opportuno, ognuno dei blocchi.
Consideriamo che la temperatura sia di:

Osservando i blocchi tramite la luce emessa dagli stessi in una stanza buia, le misure di radianza e radianza specifica avranno le seguenti caratteristiche:
- la radiazione che proviene dall'interno della cavità è sempre più intensa di quella che proviene dalla parete esterna. Se consideriamo i tre materiali prima citati come esempio, il rapporto tra la radianza della superficie esterna e quella della cavità è pari a:
- 0,259 per il tungsteno;
- 0,212 per il molibdeno;
- 0,232 per il tantalio.
- ad una fissata temperatura, la radianza del foro è identica per tutti e tre i radiatori, malgrado le radianza delle superfici esterne siano diverse.
- a differenza della radianza delle superfici esterne, la radianza di cavità, definita con Rc, varia in modo semplice con la temperatura, secondo la relazione che segue:

dove σ è una costante universale, detta costante di Stefan-Boltzmann (la tabella che segue è tratta da: http://physics.nist.gov/cgi-bin/cuu/Value?sigma|search_for=stefan+boltzmann) :
| Value | 
|
| Standard uncertainty | 
|
| Relative standard uncertainty | 
|
| Concise form | 
|
La radianza delle superfici esterne varia con la temperatura secondo una modalità "più complicata" ed è differente per diversi materiali:

dove ε è detta emissività e dipende sia dal materiale che dalla temperatura.
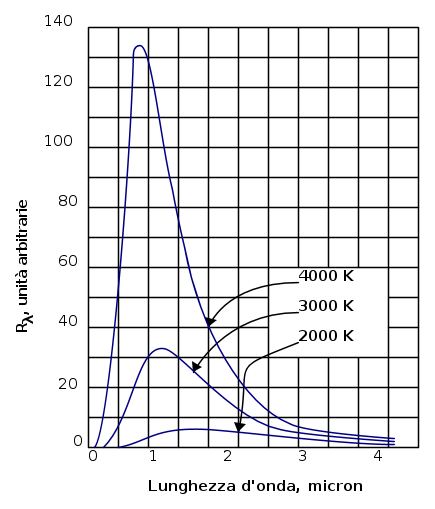
- Rλ per la radiazione di cavità varia con la temperatura secondo il modo indicato nella figura che segue, in cui le curve dipendono solo dalla temperatura e sono indipendenti dal materiale, dalla forma e dalle dimensioni della cavità:
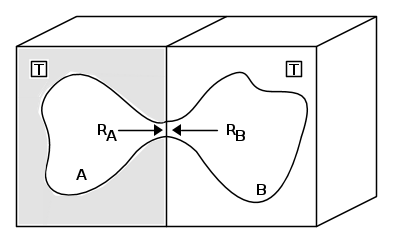
Molte delle proprietà che sono state ora citate in merito alla radiazione di cavità possono essere ricavate dalla figura che segue:
che mostra due cavità che sono state ricavate da due differenti materiali di forme arbitrarie ed aventi le pareti alla stessa temperatura T. La radiazione indicata con RA va dalla cavità A alla cavità B e la radiazione RB si muove in senso opposto. Qualora questi due trasferimenti di energia nell'unità di tempo non fossero uguali, una delle estremità del blocco comincerebbe a scaldarsi mentre l'altra comincerebbe a raffreddarsi, cosa che andrebbe a contraddire la seconda legge della termodinamica. Dobbiamo così avere:

dove Rc descrive quella che è la radiazione totale per tutte le cavità.
Inoltre anche la distribuzione in lunghezza d'onda dell'energia raggiante deve essere la stessa per entrambe le cavità della figura di cui sopra.
Questo può essere verificato immaginando di porre tra le aperture delle due cavità un filtro che sia scelto in modo tale da permettere solamente il passaggio di una banda stretta determinata di lunghezze d'onda. Con lo stesso ragionamento seguito prima, si può arrivare ad affermare che:

dove Rλc è una irradianza spettrale caratteristica di tutte le cavità.
La formula della radiazione di Planck
La spiegazione teorica della radiazione di cavità fu un problema molto dibattuto ed alcuni grandi fisici avanzarono teorie fondate sulla fisica classica, che ottenere un successo comunque limitato.
Ad esempio, la figura che segue
mostra il risultato della teoria di Wien.
L'accordo con i punti sperimentali è abbastanza buono, entro l'errore sperimentale, ma evidentemente non esatto.
La formula di Wien è:

dove c1 e c2 sono costanti che devono essere determinate sperimentalmente adattando la formula teorica ai dati sperimentali.
Nel 1900 Max Planck si accorse che modificando in modo semplice la formula di Wien si sarebbe ottenuto un perfetto accordo con i dati.
La formula di Planck, comunicata alla Società di Fisica di Berlino il 19 ottobre del 1900, è:

Questa formula, nonostante fosse molto importante, era ancora empirica e non costituiva una teoria vera e propria.
Planck giunse alla teoria considerando un modello dettagliato dei processi atomici che hanno atto sulle pareti della cavità.
Egli ipotizzò che gli atomi costituenti queste pareti si comportassero come oscillatori elettromagnetici minuscoli, ciascuno con una propria frequenza caratteristica di oscillazione.
Gli oscillatori emettono energia elettromagnetica entro la cavità e ne assorbono da essa. In questo modo dovrebbe essere possibile dedurre le caratteristiche della radiazione di cavità da quelle degli oscillatori con cui essa è in equilibrio.
Planck fu indotto a fare due ipotesi innovative sugli oscillatori atomici:
- Un oscillatore non può avere qualunque energia, ma solo energia ricavabile dalla relazione:

dove ν è la frequenza dell'oscillatore, h è una costante, chiamata ora costante di Planck, ed n è un numero, chiamato ora numero quantico, che può assumere solo valori interi.
Relativamente alla costante di Planck:
| Value | 
|
| Standard uncertainty | 
|
| Relative standard uncertainty | 
|
| Concise form | 
|
L'equazione (1) mostra che l'energia dell'oscillatore è quantizzata.
- Gli oscillatori non irradiano energia con continuità, ma solamente "a salti", o per quanti. Questi quanti di energia sono emessi quando l'oscillatore passa da un all'altro dei suoi stati quantizzati di energia.
In questo modo, se n varia di una unità, l'equazione (1) rivela che viene irradiata una quantità di energia che è pari a:

Fino a quando l'oscillatore rimane in uno dei suoi stati quantici, o stati stazionari, esso non emette né assorbe energia.
Va detto comunque che queste due ipotesi che abbiamo esposto ora furono all'epoca davvero rivoluzionarie e anche lo stesso Planck si trattenne dall'accettarle pienamente. Egli stesso infatti dichiarò a riguardo:
Basandosi quindi sulle sue due ipotesi, Planck riusci a ricavare la legge della radiazione (0) ricevendo per i risultati conseguiti il premio Nobel nel 1918. Le espressioni teoriche che ricavo per le costanti c1 e c2, fino ad allora solamente empiriche, sono:

dove k è la già citata costante di Boltzmann e c è la velocità della luce. Introducendo i valori di c1 e c2 Planck riuscì a ricavare i valori di h e k.
La teoria elaborata fu comunicata da Planck il 14 dicembre 1900 alla Società di Fisica di Berlino. Le idee di Planck furono poi rafforzate da Einstein, che nel 1905 applicò i concetti di quantizzazione dell'energia al fenomeno dell'effetto fotoelettrico.
Va infine comunque precisato che Planck, nonostante avesse quantizzato le energie degli oscillatori nelle pareti della cavità, trattava ancora la radiazione entro la cavità come un'onda elettromagnetica.
L'analisi dell'effetto fotoelettrico fatta da Einstein segnalò l'inadeguatezza, in determinate condizioni, della descrizione ondulatoria della luce.
Ma questo lo vedremo nella prossima puntata.
Bibliografia
Fisica 2. Elettromagnetismo-ottica - David Halliday, Robert Resnick

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)