Credo sia la sezione giusta, se non lo è prego i moderatori di spostare l'argomento nel luogo più consono.
Per il corso di Campi Elettromagnetici, il professore ci ha detto di focalizzare l'attenzione su un tipo di esercizi come il seguente:
E' data una lastra liscia di spessore d, lunghezza infinita,posta nel vuoto. La lastra è composta da un materiale lineare, bianisotropo, non dispersivo, non omogeneo, tale che le relazioni costitutive sono descritte da:
 ,
, 
 ,
,  ,
,  ,
, 
Arriva un'onda piana incidente lungo l'asse z dalla zona 1(ponendo l'asse z asse trasversale ai due piani che delimitano la lastra), si chiede di descrivere l'onda dentro la lastra e nella zona 3.
Io ho impostato il problema così:
Dalle equazioni di Maxwell in regime sinusoidale si avrà:


E si giunge alla risolvente per E
![[(\veebar -j\omega \alpha )\cdot \mu ^{-1}\cdot (\veebar +j\omega \beta )-\omega^{2}\varepsilon ]\cdot \boldsymbol{E} = 0 [(\veebar -j\omega \alpha )\cdot \mu ^{-1}\cdot (\veebar +j\omega \beta )-\omega^{2}\varepsilon ]\cdot \boldsymbol{E} = 0](/forum/latexrender/pictures/a70afdc933e4dba469debd6578341b9c.png)
(è omogenea perché sono in assenza di sorgenti, anche se non sono sicuro di ciò) e similmente alla risolvente per H.
Come posso continuare? Devo imporre le condizioni al contorno?
 ,
, 

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)


 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.

 e
e 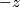 : strano che il vostro professore vi chieda di farlo come esercizio senza prima averlo spiegato a lezione.
: strano che il vostro professore vi chieda di farlo come esercizio senza prima averlo spiegato a lezione.
