venexian ha scritto:Se vuoi toglierti uno sfizio fai questi calcoli:
1. Energia cinetica della sfera all'inizio del piano scabro (pura velocità di traslazione)
2. Energia cinetica della sfera a fine strisciamento (somma energie cinetiche di traslazione e di rotazione)
3. Sono uguali?
Se la seconda è maggiore della prima abbiamo un grosso problema. Se sono uguali c'è qualcosa di sbagliato. Se sono diverse, dove è finita la loro differenza?
-
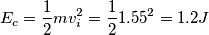
-
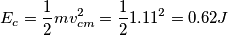
dove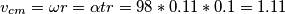
- Sono diverse, la prima è maggiore della seconda in quanto la forza di attrito ha effettuato lavoro sottraendogli energia cinetica.
Visto che ci sono faccio un'altra considerazione:
se volessi calcolare la distanza percorsa dal corpo
all'inizio del piano scabro fino al momento in cui inizia il puro rotolamento,
cioè nell'intervallo

ma calcolando la distanza
 per il solo slittamento
per il solo slittamento e la distanza
 per il solo rotolamento,
per il solo rotolamento, che se non capisco male alla fine la distanza totale percorsa nell'intervallo sarebbe
 :
:


Se ho fatto i calcoli giusti alla fine noto che la distanza totale percorsa, calcolata applicando la formula del moto uniformemente decelerato, è comprensiva anche dello spazio percorso durante il rotolamento del corpo.
Se ho un piano scabro e la velocità del centro di massa è maggiore della velocità di puro rotolamento significa che c'è strisciamento; inizialmente, quando ho scritto la prima volta il thread, credevo che la distanza percorsa con la formula del moto u.d. mi fornisse il valore dello spazio percorso SOLO in riferimento al moto di slittamento escludendo il rotolamento invece questo rappresenta lo spazio percorso dal corpo con entrambi i moti... insomma facevo confusione!

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

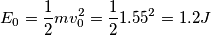


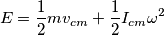
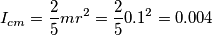



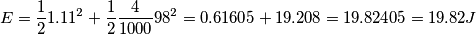
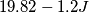 ) rappresentano il lavoro effettuato della forza di attrito?
) rappresentano il lavoro effettuato della forza di attrito?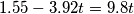 segue che
segue che 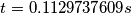

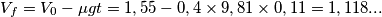
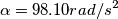
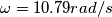
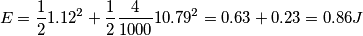


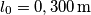
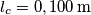
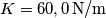
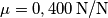
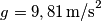
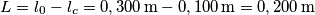
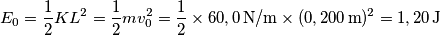
![\frac{1}{2}KL^2=\frac{1}{2}mv_0^2 \rightarrow v_0= L\sqrt[2]{\frac{K}{m} }=0,200 \, \textup{m}\sqrt[2]{\frac{60,0 \, \textup{N/m}}{1,00 \, \textup{kg}} }=1,55 \, \textup{m/s} \frac{1}{2}KL^2=\frac{1}{2}mv_0^2 \rightarrow v_0= L\sqrt[2]{\frac{K}{m} }=0,200 \, \textup{m}\sqrt[2]{\frac{60,0 \, \textup{N/m}}{1,00 \, \textup{kg}} }=1,55 \, \textup{m/s}](/forum/latexrender/pictures/2f939ce2e423ac657a34b2536065dd07.png)
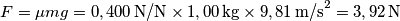
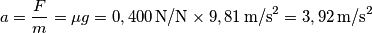

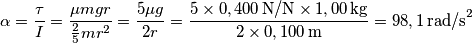
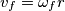
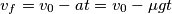
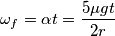

![t=\frac{2}{7}\frac{v_0}{\mu g}=\frac{2 L}{7 \mu g}\sqrt[2]{\frac{K}{m} }=\frac{2 \times 0,200 \, \textup{m}}{7 \times 0,400 \, \textup{N/N} \times 9,81 \, \textup{m/s}^2}\sqrt[2]{\frac{60,0 \, \textup{N/m}}{1,00 \, \textup{kg}} }=0,113 \, \textup{s} t=\frac{2}{7}\frac{v_0}{\mu g}=\frac{2 L}{7 \mu g}\sqrt[2]{\frac{K}{m} }=\frac{2 \times 0,200 \, \textup{m}}{7 \times 0,400 \, \textup{N/N} \times 9,81 \, \textup{m/s}^2}\sqrt[2]{\frac{60,0 \, \textup{N/m}}{1,00 \, \textup{kg}} }=0,113 \, \textup{s}](/forum/latexrender/pictures/7bdc30caffdf1262ca02613823af3257.png)
![v_f=v_0-\mu gt=v_o-\mu g\frac{2}{7}\frac{v_0}{\mu g}=\frac{5}{7}v_0=\frac{5 L}{7}\sqrt[2]{\frac{K}{m} }=\frac{5 \times 0,200 \, \textup{m}}{7}\sqrt[2]{\frac{60,0 \, \textup{N/m}}{1,00 \, \textup{kg}} }=1,11 \, \textup{s} v_f=v_0-\mu gt=v_o-\mu g\frac{2}{7}\frac{v_0}{\mu g}=\frac{5}{7}v_0=\frac{5 L}{7}\sqrt[2]{\frac{K}{m} }=\frac{5 \times 0,200 \, \textup{m}}{7}\sqrt[2]{\frac{60,0 \, \textup{N/m}}{1,00 \, \textup{kg}} }=1,11 \, \textup{s}](/forum/latexrender/pictures/5df0f0304b1937b12fd634652dcc447c.png)
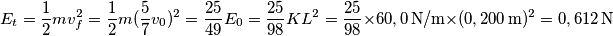
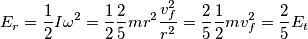
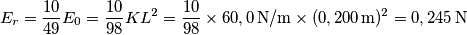
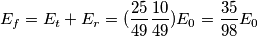




 ) e dal
) e dal