![R_{\max}=\left[\frac{P_t G A_e \sigma }{(4 \pi )^2 S_{\min}} \right]^{1/4} R_{\max}=\left[\frac{P_t G A_e \sigma }{(4 \pi )^2 S_{\min}} \right]^{1/4}](/forum/latexrender/pictures/0512f60e6aa73414527e4191804f7a27.png)
dove
 è la potenza trasmessa (integrale spaziale del vettore di poynting prodotto dall'antenna trasmittente in campo lontano),
è la potenza trasmessa (integrale spaziale del vettore di poynting prodotto dall'antenna trasmittente in campo lontano),  è il guadagno dell'antenna trasmittente,
è il guadagno dell'antenna trasmittente,  è l'area equivalente dell'antenna ricevente,
è l'area equivalente dell'antenna ricevente,  è la radar cross section del bersaglio,
è la radar cross section del bersaglio,  è la potenza ricevuta minima affinché quel particolare bersaglio possa essere rivelato alla distanza massima di
è la potenza ricevuta minima affinché quel particolare bersaglio possa essere rivelato alla distanza massima di  .
.Successivamente, l'autore afferma che:
The average radar power
 is also of interest in radar and is defined as the average transmitter power over the pulse-repetition period. If the transmitted waveform is a train of rectangular pulses of width
is also of interest in radar and is defined as the average transmitter power over the pulse-repetition period. If the transmitted waveform is a train of rectangular pulses of width  and pulse-repetition period
and pulse-repetition period  , the average power is related to the peak power by:
, the average power is related to the peak power by:
e poi subito dopo riscrive l'equazione radar sostituendo a
 l'espressione
l'espressione  (
( la chiama energia trasmessa).
la chiama energia trasmessa).Non riesco a capire come mai, sicuramente apparentemente (ma io purtroppo non vedo dove sia questo 'apparentemente'), sembra che abbia mischiato tempo e frequenza come se fossero intercambiabili.
Infatti, secondo me se vogliamo scrivere in maniera esplicita l'equazione radar, anche nella sua forma semplice come quella di sopra, essa diventa:
![R_{\max}=\left[\frac{P_t(\omega) G(\theta, \phi,\omega) A_e(\theta, \phi,\omega) \sigma(\theta, \phi,\theta_b,\phi_b,\omega) }{(4 \pi )^2 S_{\min}(\theta, \phi,\theta_b,\phi_b,\omega)} \right]^{1/4}=R_{\max}(\theta, \phi,\theta_b,\phi_b,\omega) R_{\max}=\left[\frac{P_t(\omega) G(\theta, \phi,\omega) A_e(\theta, \phi,\omega) \sigma(\theta, \phi,\theta_b,\phi_b,\omega) }{(4 \pi )^2 S_{\min}(\theta, \phi,\theta_b,\phi_b,\omega)} \right]^{1/4}=R_{\max}(\theta, \phi,\theta_b,\phi_b,\omega)](/forum/latexrender/pictures/975067351f234a9fa379dfd7ad930dac.png)
in cui
 rappresentano la direzione di puntamento comune delle due antenne,
rappresentano la direzione di puntamento comune delle due antenne,  è l'orientazione del bersaglio rispetto alle antenne,
è l'orientazione del bersaglio rispetto alle antenne,  è la pulsazione.
è la pulsazione.Seguendo quanto scritto da Skolnik avrei quindi che:

che per me non significa niente, nessun tipo di 'media'.
L'unico modo che io conosco di legare la media temporale della potenza istantanea con la potenza complessa è il seguente:

Qualcuno sa giustificare quanto affermato dall'autore?

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

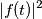 su un intervallo (al limite) infinito, sia andando ad integrare la densità spettrale di potenza; nel caso di un segnale periodico poi, come la sequenza di impulsi in oggetto (per il quale, se a base sinusoidale, la potenza di picco Pt corrisponde a metà del valore di picco massimo), ci si può limitare ad un periodo T, e il passaggio da un metodo di calcolo all'altro può essere derivato andando a rappresentare f(t) con la sua serie di Fourier in forma complessa ... o sbaglio?
su un intervallo (al limite) infinito, sia andando ad integrare la densità spettrale di potenza; nel caso di un segnale periodico poi, come la sequenza di impulsi in oggetto (per il quale, se a base sinusoidale, la potenza di picco Pt corrisponde a metà del valore di picco massimo), ci si può limitare ad un periodo T, e il passaggio da un metodo di calcolo all'altro può essere derivato andando a rappresentare f(t) con la sua serie di Fourier in forma complessa ... o sbaglio? 


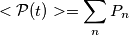
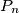 è la potenza trasportata dall'armonica
è la potenza trasportata dall'armonica  -esima, a pulsazione
-esima, a pulsazione 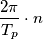 (
(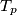 periodo di ripetizione degli impulsi).
periodo di ripetizione degli impulsi). che avevo scritto nel precedente messaggio è diventata un treno di impulsi di Dirac.
che avevo scritto nel precedente messaggio è diventata un treno di impulsi di Dirac. nell'equazione radar in luogo di
nell'equazione radar in luogo di 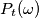 ?
?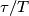 .
.

 . Il valore efficace delle due grandezze e' calcolabile semplicemente e risulta proporzionale a
. Il valore efficace delle due grandezze e' calcolabile semplicemente e risulta proporzionale a 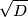 . Quando poi le moltiplichi tra di loro la radice se ne va e la potenza effettiva emessa dipende in proporzionalita' diretta da
. Quando poi le moltiplichi tra di loro la radice se ne va e la potenza effettiva emessa dipende in proporzionalita' diretta da 
