ElectroYou - la comunità dei professionisti del mondo elettrico

Indice

1 Introduzione
2 1) Cella passa basso di Sallen e Key
3 Calcolo delle sensibilita`
4 Cella di Bach
- 4.1 Sensitivity della cella di Bach
5 Mettiamo insieme i pezzi
6 Conclusioni
7 Riferimenti

Introduzione

Lo scopo di questo articolo e` di mostrare l'uso della sensitivity analysis per valutare l'effetto delle tolleranze dei componenti sulla funzione di trasferimento di un filtro, o meglio su frequenza e fattore di merito di una cella del secondo ordine usata per un filtro. La sensitivity analysis e` particolarmente importante nel progetto dei filtri, perche' tolleranze anche piccole su alcuni componenti critici possono comportare ampie variazioni nella funzione di trasferimento, facendo andare il filtro fuori specifiche.

Come esempio sara` presa una cella di Sallen e Key [1] di tipo passa basso per la quale saranno analizzati tre metodi di progetto. I risultati saranno confrontati fra di loro e poi con una derivazione del Sallen e Key, detta cella di Bach [7]. La scelta di queste celle e` stata puramente casuale, solo un modo per mostrare l'applicazione del concetto di sensibilita`. Esistono dozzine di celle attive passa basso, un elenco parziale lo si puo` trovare in [15]

L'articolo e` organizzato come segue. Nella sezione 2 vengono presentate due varianti della cella passa basso di Sallen e Key, ne viene ricavata la funzione di trasferimento, i parametri $\,\omega_0$ e $\,Q$ in funzione dei componenti e si mostrano tre strategie di progetto comunemente usate. Viene anche mostrato un esempio (qualitativo) di come varia la funzione di trasferimento di un filtro di Chebyshev del quarto ordine a causa della tolleranza dei componenti.

Nella sezione 3 si procede al calcolo delle sensibilita` dei parametri rispetto ai componenti, dapprima per il circuito generico, particolarizzando poi i risultati alle tre metodologie di progetto mostrate. Questa sezione e` particolarmente densa di conti, e la cosa buona e` che la si puo` saltare, perche' i risultati di questi conti si trovano sui manuali di progetto dei filtri.

La sezione 4 presenta la cella di Bach, e si ricava la funzione di trasferimento, le equazioni di progetto e si calcolano infine le sensibilita`. I conti su questa cella sono molto piu` semplici che sull'originale Sallen e Key.

Infine nella sezione 5 si presenta una tabella con i risultati importanti trovati: in pratica il progettista deve conoscere solo il messaggio fornito da questa tabella che i puo` sintetizzare in "non tutti i filtri con la stessa funzione di trasferimento sono uguali": ce ne sono di quelli piu` sensibili alla tolleranza dei componenti. Nella stessa sezione si mostrano anche i valori numerici delle sensibilita` valutate per una cella usata in un esempio.

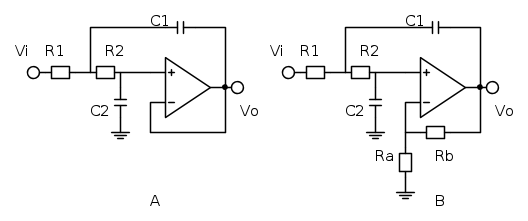
1) Cella passa basso di Sallen e Key

Due schemi di filtro passa basso del secondo ordine realizzati con cella di S&K sono presentati nella figura seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Altri schemi sono possibili, ma le loro prestazioni, per quanto riguarda l'effetto delle tolleranze, si riconducono (circa) a questi due schemi.

Il circuito A usa un voltage follower, lo schema B un amplificatore con guadagno maggiore di 1, e fornisce al progettista un grado di liberta` in piu`. Le funzioni di trasferimento dei due circuiti sono per il circuito A:

$\frac{V_o(s)}{V_i(s)}=\frac{1}{C_1C_2R_1R_2s^2+C_2(R_1+R_2)s+1}\qquad (1)$

e per il circuito B

$\frac{V_o(s)}{V_i(s)}=\frac{K}{C_1C_2R_1R_2s^2+(C_2(R_1+R_2)-C_1R_1(K-1))s+1} \qquad (2)$

dove $K=1+\frac{R_b}{R_a}$ rappresenta il guadagno dell'operazionale retroazionato da Rb ed Ra.

Una funzione passa basso del secondo ordine ha in generale questa espressione:

$\frac{V_o(s)}{V_i(s)}=K\frac{1}{\frac{s^2}{\omega_0^2}+\frac{s}{\omega_0 Q}+1}\qquad (3)$

in cui si sono messi in evidenza i parametri importanti della cella: $\,K$ guadagno in continua, $\,\omega_0$ pulsazione dei poli e $\,Q$ fattore di merito della cella.

Nella realizzazione di un filtro di ordine elevato, e` necessario realizzare celle del secondo ordine, come quella trattata qui, con un discreta precisione, altrimenti la funzione di trasferimento del filtro non risulta quella voluta. Nella figura seguente e` rappresentata in rosso la funzione di trasferimento ideale di un filtro di Chebyshev del quarto ordine, frequenza normalizzata a 1Hz e ripple in banda di 1dB, e in blu lo stesso filtro con tolleranze sui componenti dell'ordine di svariati percento.

SK.gif

Filtri di ordine piu` elevato, o con tolleranze piu` strette risentono ancora maggiormente della tolleranza dei componenti.

Uguagliando le funzioni di trasferimento trovate con la funzione generale passa basso del secondo ordine si trova la relazione fra $\omega_0,\,\,Q$ e il valore dei componenti. Il guadagno in continua $\,K$ di solito non viene imposto, ma e` scelto dal progettista per ottimizzare il circuito. Il valore di guadagno complessivo di tutto il filtro puo` essere poi messo a posto con un normale amplificatore.

Uguagliando il coefficiente di $\,s^2$ si ottiene la frequenza dei poli

$\omega_0=\frac{1}{\sqrt{R_1R_2C_1C_2}}\qquad (4)$

e dal coefficiente di $\,s$ si ottengono le relazioni del coefficiente di merito e il valore dei componenti. Per il circuito B, con guadagno $\,K$ si ha

$\begin{align}Q&=\frac{\sqrt{R_1R_2C_1C_2}}{C_2(R_1+R_2)-R_1C_1(K-1)}=\\ &=\frac{1}{\sqrt{\frac{R_2C_2}{R_1C_1}}+\sqrt{\frac{R_1C_2}{R_2C_1}}+(1-K)\sqrt{\frac{R_1C_1}{R_2C_2}}} \qquad (5) \end{align}$

mentre per il circuito A, con il voltage follower, si ha $\,K=1$ e l'espressione del fattore di merito diventa:

$Q=\frac{\sqrt{R_1R_2C_1}}{\sqrt{C_2}(R_1+R_2)}= \frac{1}{\sqrt{\frac{R_2C_2}{R_1C_1}}+\sqrt{\frac{R_1C_2}{R_2C_1}}} \qquad (6)$

Da notare che la frequenza dei poli del filtro e` data dal prodotto del valore dei componenti, mentre il valore del fattore $\,Q$ e` dato dal rapporto dei valori componenti. Questo fa si` che se in un filtro si aumentano tutti i componenti dello stesso fattore, diminuisce la frequenza $\,\omega_0$ , ma rimane invariato il $\,Q$ .

Sia dalla funzione di trasferimento trovata prima, sia dall'espressione del valore del fattore di merito, si vede che se il guadagno $\,K$ e` troppo elevato, il circuito puo` diventare instabile ed oscillare. Per questa ragione la cella di Sallen e Key viene normalmente usata quando il Q da realizzare non e` troppo elevato, tipicamente minore di 5.

Dalle espressioni ricavate, si vede come il progetto abbia in pratica due soli vincoli, $\,\omega_0$ e $\,Q$ , e ci siano da determinare 4 o 5 parametri, $R_1,\,R_2,\,C_1,\,C_2$ ed eventualmente $\,K$ . Questa liberta` di scelta e` stata utilizzata in vari modi dai progettisti, per ottenere semplificazioni di calcolo, riduzione del numero di componenti diversi da utilizzare, minimizzazione della sensitivity...

Puo` essere conveniente per facilita` di scrittura definire $R_1=R,\,R_2=mR,\,C_1=C,\,C_2=nC$ . Con questi simboli si ha

$\omega_0=\frac{1}{RC\sqrt{mn}},\quad Q=\frac{\sqrt{mn}}{n(m+1)+1-K} \qquad (7)$

Verranno ora analizzati tre metodi di progetto [14], per poi confrontarne la bonta` per quanto riguarda la sensibilita` alle variazioni dei componenti.

Progetto a componenti uguali

Una prima possibile scelta e` di prendere $\,n=m=1$ , ovvero $\,R_1=R_2=R$ e $\,C_1=C_2=C$ , riducendo cosi` il numero di componenti di valore diverso richiesti dal circuito. Con questa scelta si hanno queste espressioni per la frequenza e il fattore di merito:

$\omega_0=\frac{1}{RC}\quad Q=\frac{1}{3-K} \qquad (8)$

Si vede che il guadagno $\,K$ , cioe` le resistenze $\,R_a\text{ e }R_b$ determinano il valore del $\,Q$ , ed e` evidente, come sara` poi calcolato dopo, se il valore di $\,K$ si avvicina troppo a 3, il circuito diventa critico o instabile.

Progetto a guadagno unitario

Se si utilizzano i gradi di liberta` fissando [12] $\,K=1$ si ottiene

$\omega_0=\frac{1}{RC\sqrt{mn}}\quad Q=\frac{\sqrt{mn}}{n(m+1)} \qquad (9)$

Questa soluzione fa risparmiare due resistenze, usa l'operazionale con un guadagno unitario molto preciso, sfrutta bene la banda dell'operazionale perche' lo usa come voltage follower e ha dei vantaggi per quanto riguarda le sensibilita`. Dato che ci sono ancora essenzialmente 3 variabili $m,\,n$ e il prodotto $\,RC$ , si puo` ancora assegnare un valore a piacere, ad esempio $\,m=1$ , resistenze uguali, ottenendo

$\omega_0=\frac{1}{RC\sqrt{n}}\quad Q=\frac{\sqrt{n}}{2n}=\frac{1}{\sqrt{4n}}\qquad (10)$

Lo svantaggio di questa scelta e` il rapporto dei valori dei condensatori $\frac{1}{n}=\frac{C_1}{C_2}=4Q^2$ . Con fattori di merito appena un po' elevati, ad esempio 5, il rapporto fra i valori di capacita` diventa e di due ordini di grandezza e cresce quadraticamente con il $\,Q$ . Da notare che la funzione $Q=\frac{\sqrt{mn}}{n(m+1)}$ e` massima quando $\,m=1$ e questa scelta e` quella che, a parita` di $\,Q$ minimizza il divario fra i valori dei condensatori.

Se si fosse preso $\,n=1$ si sarebbe ottenuto $Q=\frac{\sqrt{m}}{(m+1)}\le 0.5$ , cioe` solo poli reali. Pessima scelta!

Progetto a guadagno prefissato

Una terza metodologia di progetto per questa classe di filtri e` stata sviluppata da Saraga [2] per tenere conto che non solo ci sono tolleranze e derive sui componenti passivi ma anche il guadagno dell'operazionale varia. Per minimizzare l'effetto delle variazioni di questo guadagno, Saraga ha dimostrato che bisogna prendere un valore $K=\frac{4}{3}$ , $n=\frac{1}{\sqrt{3}Q}$ e $m=\frac{Q}{\sqrt{3}}$ ottenendo queste relazioni:

$\omega_0=\frac{1}{RCQ}\qquad (11)$

da cui scelto un valore di $\,C$ oppure $\,R$ si ricavano tutti gli altri componenti:

$R_2=R\frac{Q}{\sqrt{3}}\quad C_2=C\frac{1}{\sqrt{3}Q}\qquad (12)$

Bisogna dire che dall'epoca in cui e` stato pubblicato questo articolo, gli operazionali hanno avuto miglioramenti molto maggiori rispetto a quelli dei componenti passivi, e quindi questo metodo di progetto ha attualmente meno importanza.

Calcolo delle sensibilita`

Date le formule per la valutazione dei parametri del filtro (in particolare frequenza dei poli e fattore di merito) e` possibile calcolare le sensibilita` relative, come illustrato nel primo articolo di questa serie. Si faranno solo i conti sulle espressioni generali di $\,\omega_0$ e $\,Q$ (4)(5), e si particolarizzeranno poi a seconda del caso che si sta esaminando.

Le tolleranze che possono far variare i parametri del filtro sono i valori dei componenti $R_1,\,R_2,\,C_1,\,C_2\text{ e }K\quad (13)$ . Dato che i componenti hanno una tolleranza percentuale e sia per la frequenza dei poli che per il fattore di merito sono importante le variazioni relative, sara` calcolata solo la sensibilita` relativa. Da ricordare che il valore delle derivate deve essere calcolato per i valori nominali dei componenti.

Come definito in [3], la sensibilita` relativa di una funzione $\,y$ in funzione di un parametro $\,x$ vale $S^y_x=\left . \frac{\partial y}{\partial x}\right |_\text{nom} \frac{x}{y}\qquad (14)$

Calcolando la sensibilita` della frequenza $\,\omega_0$ (4) rispetto ai vari componenti si ottiene:

$\begin{align} S_{R_1}^{\omega_0}&=\frac{\partial \left (\frac{1}{\sqrt{R_1R_2C_1C_2}}\right )}{\partial R_1}\frac{R_1}{\frac{1}{\sqrt{R_1R_2C_1C_2}}} \\ &=-\frac{1}{2R_1\sqrt{R_1R_2C_1C_2}}R_1\sqrt{R_1R_2C_1C_2}=-\frac{1}{2} \qquad (15) \end{align}$

In modo analogo si calcola la sensitivity per gli altri componenti, quella per $\,K$ invece e` nulla perche' questo parametro non compare nell'espressione di $\,\omega_0$ . Le sensibilita` relative sono quindi:

$S^{\omega_0}_{R_1,R_2,C_1,C_2}=-\frac{1}{2}\qquad S^{\omega_0}_K=0\qquad (16)$

Il calcolo delle sensibilita` del fattore di merito sono un po' piu` laboriose! In questo caso non si puo` assumere ad esempio $\,R_1=R_2=R$ : bisogna tenere distinti i valori per la derivata, e solo sostituire l'uguaglianza dei componenti alla fine del calcolo. Applicando la definizione di sentivity si ha

$\begin{align}S^Q_{R_1}=&\frac{\!\! \partial}{\partial R_1}\left(\frac{\sqrt{R_1R_2C_1C_2}}{C_2(R_1+R_2)-R_1C_1(K-1)} \right )\frac{R_1}{\frac{\sqrt{R_1R_2C_1C_2}}{C_2(R_1+R_2)-R_1C_1(K-1)}}=\\ =&\frac{\sqrt{R_1R_2C_1C_2}(C_1R_1(K - 1) + C_2(R_2 - R_1))}{2R_1(C_2(R_1+R_2)-R_1C_1(K-1))^2}\,\cdot \\ \cdot & \,\frac{R_1(C_2(R_1+R_2)-R_1C_1(K-1))}{\sqrt{R_1R_2C_1C_2}}=\\ =&\frac{C_1R_1(K - 1) + C_2(R_2 - R_1)}{2(C_2(R_1+R_2)-R_1C_1(K-1))} \qquad (17) \end{align}$

Questa e` anche la sensitivity, cambiata di segno, rispetto a $\,R_2$ , cioe`

$\,S^Q_{R_2}=-S^Q_{R_1}\qquad (18)$ .

Rispetto a $\,C_1$ , con la solita barcata di conti, i ottiene:

$\begin{align}S^Q_{C_1}=&\frac{\!\! \partial}{\partial C_1}\left(\frac{\sqrt{R_1R_2C_1C_2}}{C_2(R_1+R_2)-R_1C_1(K-1)} \right )\frac{C_1}{\frac{\sqrt{R_1R_2C_1C_2}}{C_2(R_1+R_2)-R_1C_1(K-1)}}=\\ =&\frac{\sqrt{R_1R_2C_1C_2}(C_1R_1(K - 1) + C_2(R_2 + R_1))}{2C_1(C_2(R_1+R_2)-R_1C_1(K-1))^2}\,\cdot \\ \cdot & \,\frac{C_1(C_2(R_1+R_2)-R_1C_1(K-1))}{\sqrt{R_1R_2C_1C_2}}=\\ =&\frac{C_1R_1(K - 1) + C_2(R_2 + R_1)}{2(C_2(R_1+R_2)-R_1C_1(K-1))} \qquad (19) \end{align}$

Anche in questo caso, rifacendo i conti si ottiene

$\,S^Q_{C_2}=-S^Q_{C_1}\qquad (20)$ .

Rimane da calcolare la sensibilita` rispetto alle variazioni di $\,K$ . Procedendo come al solito, si ha

$\begin{align}S^Q_{K}=&\frac{\!\! \partial}{\partial K}\left(\frac{\sqrt{R_1R_2C_1C_2}}{C_2(R_1+R_2)-R_1C_1(K-1)} \right )\frac{K}{\frac{\sqrt{R_1R_2C_1C_2}}{C_2(R_1+R_2)-R_1C_1(K-1)}}=\\ =&\frac{C_1R_1\,\sqrt{R_1R_2C_1C_2}}{(C_2(R_1+R_2)-R_1C_1(K-1))^2}\,\cdot \\ \cdot & \,\frac{K(C_2(R_1+R_2)-R_1C_1(K-1))}{\sqrt{R_1R_2C_1C_2}}=\\ =&\frac{C_1R_1K}{C_2(R_1+R_2)-R_1C_1(K-1))}=\sqrt{\frac{R_1C_1}{R_2C_2}}KQ \qquad (21) \end{align}$

E` quasi fatta, perche' volendo proprio essere pignoli bisogna ancora ricordare che il guadagno dello stadio vale $K=1+\frac{R_b}{R_a}$ e quindi bisogna ancora trovare la sensibilita` di $\,$ rispetto alle resistenze $R_a,\, R_b$ , e poi usando una proprieta` di concatenazione delle sensitivity si ottiene

$\,S^Q_{R_a}=S^Q_{K}\cdot S^K_{R_a} \qquad (22)$ .

$S^K_{R_a}=\frac{\partial\left (1+\frac{R_b}{R_a}\right)}{\partial R_a}\frac{R_a}{1+\frac{R_b}{R_a}}=-\frac{R_b}{R_a+R_b}=\frac{1-K}{K}\qquad (23)$

Mentre l'altra sensibilita` viene

$S^K_{R_b}=-S^K_{R_a}=\frac{K-1}{K}\qquad (24)$

Buone notizie: questi conti si fanno solo una volta per tutte a seconda della topologia, e si trovano gia` fatti nei manuali di progetto dei filtri, dove sono riportate le formule pratiche da usare che saranno trovate per i vari criteri di progetto. Qui si fa solo vedere come vengono ricavare le espressioni.

Sensibilita` per il progetto a componenti uguali

Si sostituiscono le condizioni $\,R_1=R_2=R$ e $\,C_1=C_2=C$ nelle espressioni delle sensitivity $\,S^Q_{(R,C,K)}$ calcolate in (17)(19)(21) si ottiene:

$S^Q_{R_1}=-S^Q_{R_2}=\frac{1-K}{2(K-3)}=Q-\frac{1}{2}\qquad (25)$

Nell'ultimo passaggio si e` sfruttato l'equazione (8) invertita:

$K=3-\frac{1}{Q}\quad (26)$

Per la sensibilita` verso i cambiamenti delle capacita`, con le stesse condizioni, si ha:

$S^Q_{C_1}=-S^Q_{C_2}=\frac{1+K}{2(3-K)}=2Q-\frac{1}{2} \qquad (27)$

Infine per i cambiamenti del fattore di qualita` dovuti al guadagno si ha:

$S^Q_{K}=QK=3Q-1 \qquad (28)$

Come si vede di mano in mano che il Q della cella aumenta le sensibilita` aumentano anch'esse e anche in modo drammatico. Bisogna dire che la sensibilita` verso il guadagno $\,K$ in realta` va ancora riportata alle variazioni delle resistenze di retroazione. Partendo dalle sensibilita` del guadagno rispetto alle resistenze di retroazione, e sostituendo il legame di questo specifico circuito fra guadagno e fattore di merito si ottiene:

$S^K_{R_b}=-S^K_{R_a}=\frac{K-1}{K}=\frac{2Q-1}{3Q-1}\qquad (29)$

e combinando questa sensibilita` con quella del $\,Q$ in funzione di $\,K$ (28) si ha

$S^Q_{R_b}=-S^Q_{R_a}=S^Q_{K}S^K_{R_b}=\frac{2Q-1}{3Q-1}(3Q-1)=2Q-1\qquad (30)$

Sensibilita` per il progetto a guadagno unitario

In questo caso le condizioni di realizzazione sono $\,R_1=R_2=R$ e $\,K=1$ . La sensibilita` della frequenza dei poli non cambia per queste tre topologie e rimane sempre ad un valore basso. Invece per quanto riguarda il fattore di merito si ha:

$\,S^Q_{R_1}=S^Q_{R_2}=0\qquad (31)$

Ovvero per piccoli spostamenti intorno al valore nominale, l'effetto della tolleranza delle resistenze e` nullo! Questa e` un'ottima cosa, che pero` genera una curiosita`: se la sensitivity e` nulla, e cambio un pochino una resistenza, non avro` piu` che $\,R_1=R_2=R$ e quindi non sara` piu` vero che la sensitivity e` nulla.

In effetti se si cambia una resistenza la sensitivity non sara` piu` uguale a zero, ma l'effetto complessivo non sara` proporzionale alla tolleranza della resistenza, del tipo $\,\delta_Q=S^Q_R \delta_R\quad (32)$ ma sara` una espressione del tipo $\,\delta_Q= S^{\prime Q}_R \delta_R^2\quad (33)$ in cui entra il quadrato della tolleranza, e $\,S^{\prime Q}_R$ e` la sensitivity del secondo ordine. In pratica il termine e` trascurabile.

La sensibilita` rispetto alle variazioni del valore dei condensatori e`

$S^Q_{C_1}=-S^Q_{C_2}=-\frac{1}{2}\qquad (34)$

La sensibilita` verso $\,K$ e` praticamente nulla perche' il guadagno unitario non dipende da resistenze ma solo dall'elevatissimo guadagno dell'operazionale.

Questo secondo progetto e`, per quanto riguarda le sensibilita`, di gran lunga migliore del primo, al costo di dover usare condensatori precisi e di valori abbastanza diversi se il $\,Q$ e` elevato.

Sensibilita` per il progetto a guadagno prefissato

Anche in questo circuito la sensibilita` della frequenza alla variazione dei valori dei componenti e` sempre la stessa (16).

Per quanto riguarda il $\,Q$ , sostituendo le condizioni (12) $R_1=R,\,\,R_2=R\frac{Q}{\sqrt{3}}$ e $C_1=C,\quad C_2=C\frac{1}{\sqrt{3}Q}$ nonche' $K=\frac{4}{3}$ si ottiene:

$S^Q_{R_1}=-S^Q_{R_2}=\frac{\sqrt{3}}{3}Q-\frac{1}{2}\approx .58Q-.5\qquad (35)$

e per le capacita`

$S^Q_{C_1}=-S^Q_{C_2}=\frac{\sqrt{3}}{3}Q+\frac{1}{2}\approx .58Q+.5\qquad (36)$

e infine per il guadagno:

$S^Q_{K}=\frac{4\sqrt{3}}{3}Q\qquad (37)$

Per trovare la sensibilita` rispetto alle resistenze di retroazione, procedendo come prima si trova la sensibilita` delle variazioni di guadagno rispetto alle resistenze, ricordando che in questo caso il guadagno e` prefissato:

$S^K_{R_b}=-S^K_{R_a}=\frac{K-1}{K}=\frac{\frac{4}{3}-1}{\frac{4}{3}}=\frac{1}{4}\qquad (38)$

e combinando insieme le sensibilita` si ha

$S^Q_{R_b}=-S^Q_{R_a}=S^Q_{K}S^K_{R_b}=\frac{4\sqrt{3}}{3}Q \frac{1}{4}=\frac{\sqrt{3}}{3}Q\approx .58Q\qquad (39)$

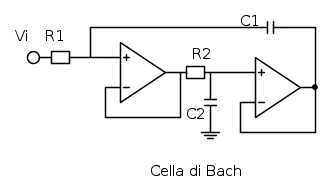
Cella di Bach

Nel 1969, a distanza di 4 mesi, sulla stessa rivista sono stati pubblicati due articoli [4][5] praticamente identici da parte di autori che non sapevano che altri stavano lavorando sullo stesso progetto.

Il primo a pubblicare, Geffe, si e` anche incazzato un pochino, cercando di stabilire che l'idea era venuta prima a lui, gli altri hanno risposto che non sapevano che fosse in corso di pubblicazione il suo articolo e che anche loro avevano trovato quel risultato l'anno prima [6].

La cosa buffa e` che nessuno dei due cita un articolo del 1960 in cui questo circuito era praticamente gia` stato descritto da Bach [7]. Dopo Bach la stessa topologia era stata riscoperta da Kundert [7a] nel 1964.

La cella passa basso in versione Bach e` in figura:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

In questa cella e` stato aggiunto un voltage follower per far si` che il gruppo $\,R_2C_2$ non carichi la rete formata da $\,R_1C_1$ . La funzione di trasferimento e` ancora un passa basso del secondo ordine, e vale

$\frac{V_o(s)}{V_i(s)}=\frac{1}{C_1C_2R_1R_2s^2+C_2R_2s+1}\qquad (40)$

La frequenza dei poli e il loro fattore di merito in questo caso valgono, al solito con $R_1=R,\,\,R_2=m R$ e per i condensatori $C_1=C,\,\,C_2=n C:$

$\omega_0=\frac{1}{\sqrt{R_1R_2C_1C_2}}=\frac{1}{RC\sqrt{mn}}\qquad (41)$

$Q=\frac{\sqrt{R_1R_2C_1C_2}}{C_2R_2}=\sqrt{\frac{R_1C_1}{R_2C_2}}=\frac{1}{\sqrt{mn}}\qquad (42)$

Le equazioni di progetto sono semplici, grazie al disaccoppiamento introdotto dal voltage follower. Si hanno 4 incognite e due vincoli. Un modo conveniente di scriverle potrebbe essere di mantenere espresse le costanti di tempo $\,R_1C_1$ e $\,R_2C_2$ in questo modo:

$R_1C_1=\frac{Q}{\omega_0}\qquad R_2C_2=\frac{1}{\omega_0 Q}\qquad (43)$

Sensitivity della cella di Bach

Il conto delle sensitivity della cella di Bach e` molto semplice. Le sensibilita` di $\,\omega_0$ e` ancora come per gli altri circuiti (16): Le cose interessanti capitano per le sensitivies del fattore di merito:

$S^Q_{R_1}=\frac{\partial Q}{\partial R_1}\frac{R_1}{Q}=\frac{\!\!\partial}{\partial R_1}\left (\sqrt{\frac{R_1C_1}{R_2C_2}}\right )\frac{R_1}{\sqrt{\frac{R_1C_1}{R_2C_2}}} =\frac{\sqrt{C_1}}{2\sqrt{R_1R_2C_2}}\,R_1\sqrt{\frac{R_2C_2}{R_1C_1}}=\frac{1}{2} \qquad (44)$

Per tutte le sensibilita` del $\,Q$ si ha:

$S^Q_{R_1}=-S^Q_{R_2}=S^Q_{C_1}=-S^Q_{C_2}=\frac{1}{2} \qquad (45)$

Questo e` un ottimo risultato: tutte le sensitivities sono basse, e non dipendono dal $\,Q$ . Inoltre non ci sono vincoli sul valore delle resistenze e capacita`, il che vuol dire che anche con fattori di merito elevati, possiamo usare due capacita` di valori ancora abbastanza vicini, e due resistenze anche non troppo separate per valore, dell'ordine di $m=n=\frac{1}{Q}$ , mentre nel progetto con amplificatore a guadagno unitario si aveva $n=\frac{1}{4Q^2}$

Mettiamo insieme i pezzi

Dopo questo tour de force di conti, (che per fortuna sono gia` tutti fatti sui vari manuali e testi, ad esempio [8][9][10][11] e migliaia di altri, possiamo preparare una tabella in cui vengono confrontate le sensibilita` dei vari circuiti.

Sensibilita`	$R_1=R_2,\,C_1=C_2$	$R_1=R_2, \,K=1$	Saraga	Bach
$S^{\omega_0}_{R_1,R_1,C_1,C_2}$	$-\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{1}{2}$
$S^{\omega_0}_{R_b,R_a}$	$\,0$	$\,0$	$\,0$	$\,0$
$S^Q_{R_1}=-S^Q_{R_2}$	$Q-\frac{1}{2}$	$\,0$	$.58Q-\frac{1}{2}$	$\frac{1}{2}$
$S^Q_{C_1}=-S^Q_{C_2}$	$2Q-\frac{1}{2}$	$\frac{1}{2}$	$.58Q+\frac{1}{2}$	$\frac{1}{2}$
$S^Q_{R_b}=-S^Q_{R_a}$	$2Q-1\,$	N.A.	$\, .58Q$	N.A.

Si vede immediatamente che le celle a guadagno unitario e quella di Bach si comportano molto bene rispetto alle tolleranze dei componenti. La cella a guadagno unitario ha come inconveniente il dover usare per $\,Q$ elevati delle capacita` di valore molto diverso fra di loro. La cella di Bach costa due operazionali al posto di uno soltanto.

La cella a componenti uguali si comporta decisamente male per valori di $\,Q$ elevati, la cella di Saraga va meglio, e riduce la sensibilita` anche le variazioni di guadagno dell'operazionale. Come gia` detto, con operazionali discreti moderni questo problema non e` piu` molto attuale.

Come esempio numerico si usera` una delle due celle del filtro di Chebyshev usato come esempio all'inizio di questo articolo. Una delle due celle ha $\,Q=3.559$ , fattore di merito relativamente elevato, e faremo i conti su questa. L'altra ha $\,Q=0.785$ e non presenta particolari difficolta` realizzative.

Nella tabella seguente, sono riportati i valori numerici ricavati dalle espressioni analitiche:

Sensibilita`	$R_1=R_2,\,C_1=C_2$	$R_1=R_2, \,K=1$	Saraga	Bach
$S^{\omega_0}_{R_1,R_1,C_1,C_2}$	$\,-.5$	$\,-.5$	$\,-.5$	$\,-.5$
$S^{\omega_0}_{R_b,R_a}$	$\,0$	$\,0$	$\,0$	$\,0$
$S^Q_{R_1}=-S^Q_{R_2}$	$\,3.06$	$\,0$	$\,2.05$	$\,.5$
$S^Q_{C_1}=-S^Q_{C_2}$	$\,6.61$	$\,.5$	$\,2.55$	$\,.5$
$S^Q_{R_b}=-S^Q_{R_a}$	$\,6.11\,$	N.A.	$\, 2.05$	N.A.

Sensibilita` dell'ordine di svariate unita` sono decisamente critiche: una tolleranza ad esempio dell'1% sul valore di un componente viene ingrandita a parecchi percento di errore sul Q del circuito. Ad esempio un filtro che richieda dei fattori di qualita` elevati non puo` essere realizzato con componenti al 5% e topologie che moltiplicano le tolleranze.

Se si dovesse salire a fattori di merito della decina o piu`, l'unico candidato di questa famiglia rimane la cella di Bach, oppure si passa su altre topologie di circuiti.

Esempi di progetto con celle di Sallen e Key si trovano in molte application notes, ad esempio in [13] OA-27 di National.

Conclusioni

In questo articolo sembra mancare un passaggio, perche' si e` mostrato un esempio di funzione di trasferimento "rovinata" dalle tolleranze, ma nel seguito ci si e` fermati al calcolo dell'effetto delle tolleranze sui parametri della singola cella, non si e` guardato l'effetto complessivo sulla funzione di trasferimento. La ragione di questa mancanza e` duplice. Da un lato non volevo allungare troppo questo articolo con un'altra sezione per calcolare la sensibilita` della funzione di trasferimento alle variazioni delle celle del secondo ordine che le costituiscono.

La seconda ragione e` che di solito il progettista valuta la bonta` e l'applicabilita`di una cella attiva "da sola", senza pensarla usata in un filtro con altre celle. Le informazioni su fattore di merito e frequenza sono spesso sufficienti alla scelta della topologia.

Il legame fra fattori della cella e funzione di trasferimento complessiva puo` essere calcolato analogamente a quanto fatto in questo articolo (un po' piu` macchinoso perche' entrano funzioni di variabile complessa), ma piu` spesso la valutazione sulla funzione di trasferimento e` fatta con simulazione numerica.

Come nota finale, il problema della sensitivity nella realizzazione dei filtri esiste non solo per i filtri analogici (sia attivi che passivi), ma anche per i filtri numerici o digitali che dir si voglia. Questi filtri sono costituiti da un programma o da uno hardware di calcolo, e sembrerebbe che le tolleranze nel mondo digitale non dovrebbero esistere. In realta` c'e` tuttavia il problema che i coefficienti del filtro sono rappresentati su un numero finito di bit (e qualche volta neanche troppo elevato) e la granularita` dei numeri rappresentati con un numero finito di bit puo` dare errori nella funzione di trasferimento del filtro o addirittura, in qualche raro caso, instabilita`.

Riferimenti

[1] Sallen, R.P. and Key, E.L., "A Practical Method of Designing Active Filters," IRE Trans. on Circuit Theory, vol. CT-2, pp.74 to 85, March 1955

[2]Saraga, W., “Sensitivity of 2nd-Order Sallen-Key-Type Active RC Filters,” Electron. Lett. 3(10), October 1967, pp. 442–444.

[3] IsidoroKZ, "Sensitivity I - Definizioni e Applicazioni" , Electroyou.

[4] Geffe P. R., "A Q-invariant Active Resonator", Proc. IEEE (Lett.), Vol. 57, pag. 1442, August 1969

[5] Soderstrand M. A. and Mitra S. K., "Extremely Low Sensitivity Active RC Filter", Proc. IEEE (Lett.), Vol. 57, pag. 2175, December 1969.

[6] Geffe, P.R.; Soderstrand, M.A.; Mitra, S.K.; "Comments on "Extremely Low Sensitivity Active RC Filter" and "A Q-Invariant Active Resonator"", Proc. IEEE (Lett.), Vol. 58, pag. 824, May 1970

[7] Bach, R. E., “Selecting R-C Values for Active Filters”, Electronics 33, pp. 82–83, May 13, 1960

[7a] Kundert W.R., "The RC Amplifier-Type Active Filter: A Design Method for Optimum Stability" IEEE Trans. on Audio, vol. AU-12, pag. 66-71, Jul-Aug 1964.

[8] Franco, S. Design with Operational Amplifiers and Analog Integrated Circuits, 3rd Ed., McGraw-Hill, 2002

[9] Daryanani, G., Principles of Active Network Synthesis and Design, Wiley 1976

[10] Deliyannis, T., Continuous-Time Active Filter Desig, CRC Press LLC, 1999

[11] Huelsmann L.P. and Allen P.E., Introduction to the Theory and Design of Active Filters, McGraw-Hill, 1980.

[12] Maxim IC. "Minimizing Component-Variation Sensitivity in Single Op Amp Filters", AN-738, Mar 2001

[13] Kumen B., "Low-Sensitivity, Lowpass Filter Design", National Semiconductors, OA-27, August 1996.

[14] Karki J., "Analysis of the Sallen-Key Architecture", Texas Instruments, Appl. Rep. SLOA024B, Sept 2002.

[15] Circuitsarchive Second Order Low-Pass

ElectroYou - la comunità dei professionisti del mondo elettrico

Sensitivity III - Filtri attivi

Indice

Introduzione

1) Cella passa basso di Sallen e Key

Progetto a componenti uguali

Progetto a guadagno unitario

Progetto a guadagno prefissato

Calcolo delle sensibilita`

Sensibilita` per il progetto a componenti uguali

Sensibilita` per il progetto a guadagno unitario

Sensibilita` per il progetto a guadagno prefissato

Cella di Bach

Sensitivity della cella di Bach

Mettiamo insieme i pezzi

Conclusioni

Riferimenti

Inserisci un commento

Argomenti correlati

Tag Cloud

Informazioni

Seguici

Pubblicità

Credits