AK47

voti

Bipoli fondamentali

pubblicato 12 anni fa,
8.093 visualizzazioni,
commenti: 19,
PDF,
Mostra indice

Introduzione

Prendiamo un phone e colleghiamolo alla presa.
Abbiamo appena preso un bipolo, e abbiamo fatto in modo che interagisse con un sistema elettrico.
Che cos'è quindi un bipolo?
E' un componente, o un insieme di componenti riconducibili a uno equivalente, collegato al resto del circuito in due punti soltanto, detti morsetti.
I bipoli sono definiti in base al legame tra la tensione ai loro capi e l'intensità di corrente che li attraversa. Espliciteremo quindi, come si era accennato alla fine del precedente articolo, la funzione I=f(V) o la sua inversa, V=g(I) discutendone anche la matrice energetica.

Si può immaginare di ricavare il legame applicando al bipolo una tensione nota variabile e misurare la corrente assorbita con un amperometro ideale, oppure iniettare nel bipolo un'intensità nota e misurare la tensione con un voltmetro ideale, elaborando successivamente la tabella di valori di tensione e di corrente.

La curva che si ottiene rappresentando la tensione in funzione della corrente, o viceversa, è detta caratteristica esterna del bipolo. Nei successivi paragrafi vedremo le caratteristiche esterne dei bipoli fondamentali.
Definiremo quindi i bipoli assiomaticamente, cioè in base alle loro proprietà come elementi circuitali.
Tensione e corrente sono, nel caso generale dipendenti dal tempo, ed indicate con:

$\begin{matrix}i(t)\;\;\;\text{e}\;\;\;v(t)\end{matrix}$

ma ci si soffermerà sul caso, particolare ma importante, in cui sono costanti, condizione che le definisce comunemente come grandezze continue. Le indicheremo allora con le lettere maiuscole:

$\begin{matrix}I\;\;\;\text{e}\;\;\;V\end{matrix}$

Nei prossimi articoli verrà esaminato un altro caso particolare, ma estremamente importante, della loro variazione nel tempo secondo una legge che matematicamente assume l'espressione di una funzione sinusoidale.

Tipi di bipolo

I bipoli elettrici possiamo suddividerli in tre categorie in base al modo in cui essi trattano l'energia

Bipoli generatori

I generatori forniscono energia alle cariche elettriche prelevandola da una sorgente esterna che definisce il tipo di generatore (elettromeccanico, elettrochimico, fotoelettrico ecc.). Sono pertanto gli elementi di interfaccia tra il circuito elettrico e l'esterno, una porta attraverso cui l'energia fluisce trasformandosi da non elettrica in elettrica.
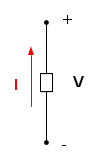
In un bipolo generatore, la corrente convenzionale esce dal terminale a potenziale più alto. Contrassegnare in questo modo il bipolo, significa adottare la convenzione del generatore:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Nei generatori reali, cioè quelli che si è in grado di costruire, una parte dell'energia entrante nel sistema elettrico ne esce immediatamente ed inevitabilmente sotto forma di calore. L'entità di questa perdita definisce il rendimento elettrico del generatore. In termini di potenza, se $P i$ è la potenza non elettrica in ingresso e $P p$ è la totale potenza dissipata in calore, il rendimento è dato da $\eta=1-\frac{P_p}{P_i}$ , cioè è sempre minore di uno.

Bipoli utilizzatori

Utilizzatori sono i bipoli che prelevano energia dalle cariche, la estraggono cioè dal circuito elettrico, trasformandola da elettrica in altra forma (meccanica, chimica, calore, luce ecc.). Sono dunque anch'essi interfacce tra il sistema elettrico e l'esterno.
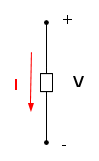
In un bipolo utilizzatore la corrente convenzionale entra dal terminale a potenziale più alto.
Contrassegnare in questo modo la tensione e la corrente significa scegliere per il bipolo la convenzione dell'utilizzatore.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Tutta l'energia elettrica entrante nel bipolo utilizzatore ne esce: una parte è inevitabilmente calore, l'altra può essere di varia natura e caratterizza l'utilizzatore (es: se meccanica è un motore elettrico). Il calore appare come una perdita di energia e la sua entità definisce il rendimento elettrico dell'utilizzatore, nello stesso modo in cui è stato definito per i generatori. In tal caso la $P i$ è naturalmente di tipo elettrico.

Bipoli accumulatori

Sono bipoli in grado di immagazzinare energia elettrica nella forma di tipo potenziale o cinetica, e non scambiano energia con componenti esterni al sistema elettrico ma solo con gli altri componenti del sistema elettrico.
Condensatore e induttore infatti, nelle loro versioni ideali, immagazzinano rispettivamente energia elettrostatica (tipo potenziale), e energia magnetica (tipo cinetico). Approfondiremo successivamente questi aspetti.

Generatori ideali

Si definisce generatore ideale (o indipendente) un bipolo che mantiene inalterata una delle due grandezze elettriche, qualunque sia il valore dell'altra. Ciò implica l'assenza di potenza persa sotto forma di calore, per cui i generatori ideali, e solo essi, hanno un rendimento unitario. Sono di due tipi: di tensione e di corrente.

Generatore ideale di tensione

E' un bipolo, che presenta ai morsetti una tensione completamente indipendente da tutto ciò che può essere collegato ad esso, quindi dalla intensità di corrente da cui può essere attraversato.
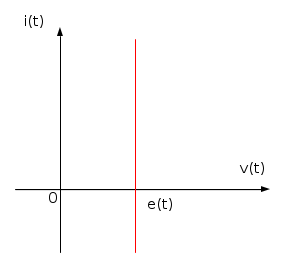
Ecco la sua rappresentazione circuitale, e la sua caratteristica esterna riferita ad un istante qualsiasi:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il modello matematico è dunque

$v(t) = e(t) \; \; \; \; \quad {\rm{ }}\forall {\rm{ }} \, i(t)$

I generatori sono tali quando erogano potenza elettrica. La potenza erogata è data da $p (t) = v (t) i (t) = e (t) i (t)$ .
Con la convenzione del generatore tale espressione è positiva, quindi il bipolo è un effettivo generatore, se i(t) esce dal polo positivo. Ma i(t) può essere qualsiasi ( $\forall {\rm{ }} \, i(t)$ ) , quindi anche entrante, perciò negativa rispetto al verso fissato. In tal caso la potenza erogata è negativa, quindi assorbita, ed il bipolo è un utilizzatore detto attivo, in quanto la potenza è trasformata in una forma diversa dal calore, meccanica ad esempio nel caso di motori.
In definitiva il generatore ideale di tensione può rappresentare sia un effettivo generatore che un utilizzatore attivo. Attivo perché, come i generatori, genera nel circuito una tensione elettrica che però si oppone alla corrente.
Per le grandezze continue si scriverà ovviamente:

$\begin{matrix}P=VI=EI\end{matrix}$

La tensione e(t) che il bipolo impone, è anche detta forza elettromotrice nel caso si tratti di un generatore; forza controelettromotrice nel caso di un utilizzatore attivo.

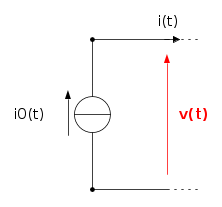
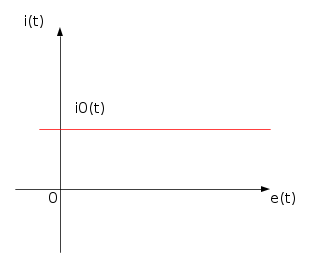
Generatore ideale di corrente

E'un bipolo, la cui intensità di corrente è completamente indipendente da tutto ciò che può essere collegato ai morsetti, quindi dalla tensione elettrica tra essi.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il modello matematico, è dunque

$i(t) = {i_0}(t) \; \; \; \; \; \quad {\rm{ }}\forall {\rm{ }} \, v(t)$

Per quanto riguarda la potenza erogata dal generatore ideale di corrente, valgono le stesse considerazioni fatte per quello di tensione. Per approfondire: Esempio 1

Bipolo utilizzatore puro

E' il bipolo utilizzatore che rappresenta il consumo di energia elettrica. In esso le cariche perdono l'energia posseduta. Il componente che lo rappresenta è il

Resistore

E' un puro dissipatore e rappresenta, fondamentalmente, l'effetto termico della corrente elettrica tipico dei conduttori.
Il movimento delle cariche libere, per effetto dell'aumento degli urti reciproci e con gli elementi del reticolo, sviluppa calore. Il valore dell'intensità di corrente è conseguente ad un equilibrio dinamico tra l'energia ricevuta dalle cariche da parte del generatore e l'energia da esse dissipata in calore. L'aumento dell'intensità implica un aumento dell'energia dissipata, quindi un aumento dell'energia fornita dal generatore, cioè della tensione.
E' ciò che succede ad un corpo che si muove in un fluido: la sua velocità è determinata dall'equilibrio tra l'energia ricevuta e quella dissipata per attrito. Il mantenimento di un certo valore dell'energia cinetica richiede l'immediato ripristino di quella parte di essa che si trasforma in calore.
Il conduttore può essere paragonato ad un tubo in cui c'è un fluido (gli elettroni liberi) che può essere posto in movimento (corrente) da una differenza di pressione (la tensione) tra le sue sezioni terminali (i poli).

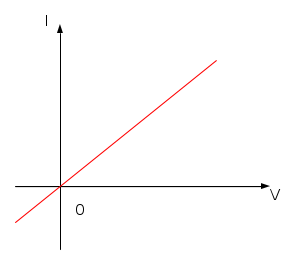
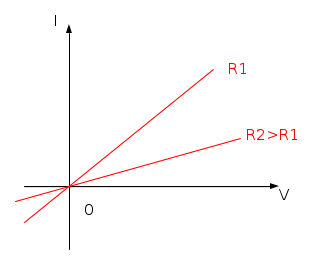
Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

La caratteristica esterna è una retta passante per l'origine, la cui inclinazione dipende dal valore della resistenza, come mostrato nella seguente figura

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Maggiore è la resistenza, minore è la pendenza della retta.
Nelle figure precedenti si è assunto $v A B (t) = V$ , costante ed $i (t) = I$ , costante e si è adottata la convenzione di utilizzatore.
L'equazione della caratteristica definisce il modello matematico del resistore

$\begin{matrix}v(t)=Ri(t)\end{matrix}$

che corrisponde alla

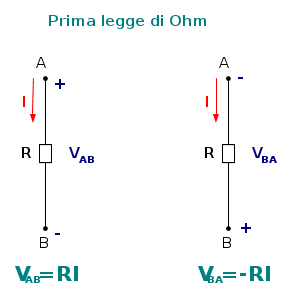
Prima legge di Ohm

$R=\frac{V}{I}$

R, valore della resistenza, è un numero positivo. La sua unità di misura è l'ohm (Ω), cge, dimensionalmente, è volt diviso ampere:

$\begin{matrix}\Omega=\text{V} \, \text{A}^{-1}\end{matrix}$

Spesso è utile utilizzare l'inverso della resistenza che prende il nome di conduttanza:

$G=\frac{1}{R}$

la cui unità di misura è il siemens:

$\begin{matrix}\text{S}=\Omega^{-1}\end{matrix}$

A tal proposito qui un'interessante riflessione.
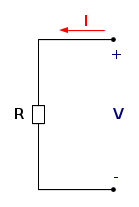
Spesso ci si dimentica che la precedente equazione è scritta per la convenzione di utilizzatore. Se si assume quella di generatore occorre invece scrivere $V = - R I$ , come evidenziato nella figura che segue

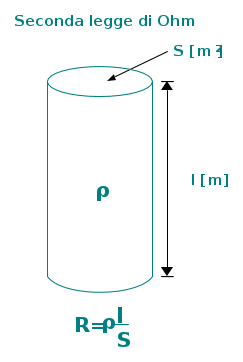
Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Della resistenza ohmica si può esaminare la dipendenza dalle dimensioni geometriche del conduttore e dalle sue proprietà fisiche. Per un conduttore prismatico o cilindrico, la resistenza è proporzionale al rapporto tra la lunghezza assiale $l$ , e l'area della sezione trasversale $S$ . Definiamo infatti la

Seconda legge di Ohm

$R=\rho \frac{l}{S}$

dove ρ è la resistività del materiale. I valori di ρ sono tabellati, e ovviamente tale parametro varia da materiale a materiale. La resistività si misura in ohm per metro. L'inverso della resistività è la conduttività, la cui unità di misura è siemens diviso metro.

Potenza ed energia

Se calcoliamo la potenza otteniamo le espressioni della legge di Joule:

$P=VI=\frac{V^2}{R}=RI^2$

Essendo R un numero positivo, dipendendo dal quadrato delle grandezze elettriche, la potenza è sempre positiva. Non poteva risultare diversamente del resto, essendo il resistore, come già detto, un puro consumatore di energia ed avendo assunto la convenzione di utilizzatore. L'energia può manifestarsi sotto forma di calore, ma anche di altro tipo; se pensiamo a una lampadina ad incandescenza, ad esempio, una piccola parte diventa energia luminosa.
Le resistenze possono quindi anche per rappresentare un carico che non dissipa energia sotto forma di calore, ma la trasforma, ad esempio, in energia meccanica. Si parla in tal caso di resistenza fittizia. Tipico è il caso del circuito equivalente del motore asincrono, ma questa è un'altra storia...
L'energia consumata dipende ovviamente dal tempo:

$\begin{matrix}W=Pt\end{matrix}$

Variazione della resistenza in funzione della temperatura

La resistività e di conseguenza la resistenza dipendono dalla temperatura secondo la legge:

$\begin{matrix}\rho _{\theta}=\rho _0(1+\alpha \theta)\end{matrix}$

Dove:

$ρ θ$ : resistività alla temperatura di $θ$ °C ;

$ρ 0$ : resistività alla temperatura di 0 °C ;

$α$ : coefficiente di temperatura del materiale, ovvero la variazione relativa di resistività per ogni grado di temperatura, che dipende dalla temperatura di riferimento: la sua unità di misura è perciò l'inverso del grado: °C^-1. In tabella sono riportati le caratteristiche di alcuni materiali alla temperatura di 0 °C:

Materiale	$ρ 0$ : resistività del materiale: Ω mm²/m	$α$ : coefficiente di temperatura: °C^-1 $\cdot$ 10^-3
Rame	0,017	4,3
Alluminio	0,027	4,5
Oro	0,021	4
Argento	0,015	4,1
Ferro	0,096	6,5
Tungsteno	0,051	4,8
Nichel-Cromo	1,06	0,1
Manganina	0,4	0,01
Carbone	50	-0,4
Silicio	2,5 $\cdot$ 10⁹	negativo
Germanio	5 $\cdot$ 10⁵	negativo

Bisogna notare che nei materiali conduttori il coefficiente di temperatura è positivo (PTC); per alcuni materiali è invece negativo (NTC). In questi ultimi c'è una diminuzione della resistenza all'aumentare della temperatura: è tipico dei semiconduttori dove l'aumento di temperatura aumenta il numero di cariche libere, mascherando l'aumento della perdita di energia per attrito che comunque continua a persistere.
Riporto per approfondire la seguente discussione:

Legame tra resistività e temperatura nei conduttori

Approfondimenti sul resistore

Esercizio
Note sui Resistori by mir
Infantilmente sul concetto di resistenza elettrica by elettrodomus
Resistenza di un trapezio: due approssimazioni per un problema tosto by IsidoroKZ

Esempio 1

Bipoli degeneri

Sono bipoli in cui una delle due grandezze è nulla mentre l'altra può assumere valori qualsiasi. Non sono sede pertanto di alcuna trasformazione energetica, quindi non possono essere considerati né generatori né utilizzatori ma, matematicamente, possono essere ricondotti alle situazioni estreme sia degli uni che degli altri.

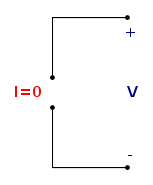
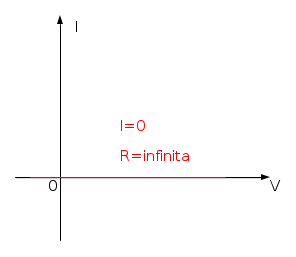
Circuito aperto ideale

Bipolo interessato da corrente nulla qualsiasi sia la tensione ai suoi capi. L'equazione che lo descrive è:

$\begin{matrix}I=0\end{matrix}$

Può essere visto come un generatore ideale corrente la cui corrente è nulla, oppure come un perfetto isolante che potremmo definire conduttore di resistenza infinita (un ossimoro, se ci pensiamo).

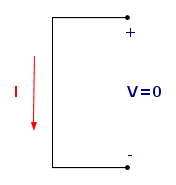
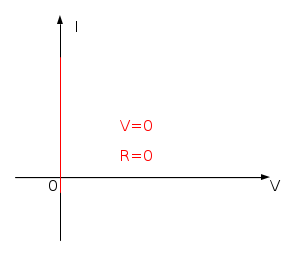
Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Corto circuito ideale

Bipolo che mantiene tensione nulla qualsiasi sia la corrente che lo attraversa. L'equazione che lo descrive è:

$\begin{matrix}V=0\end{matrix}$

Può essere visto come un generatore ideale di tensione la cui f.e.m. è nulla, oppure come un conduttore di resistenza nulla.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il bipolo condensatore

E' il bipolo accumulatore di energia elettrica sotto forma di energia potenziale. E' costituito da due conduttori, detti armature, cui fanno capo i due poli, separati da un isolante.

Quando il condensatore possiede energia elettrica le armature hanno carica uguale ed opposta, il cui valore assoluto è detto carica del condensatore. Tra le armature esiste allora una tensione $v A B (t)$ , e la carica del condensatore $q (t)$ è proporzionale ad essa in ogni istante. La costante di proporzionalità è un numero positivo è detta capacità del condensatore:

$C=\frac{q(t)}{v_{AB}(t)}$

Poiché C è positivo, $q (t) > 0$ se $v A B (t) > 0$ è la carica dell'armatura A.
C si misura in farad, che è coulomb diviso volt :

$\begin{matrix}\text{F}=\text{C} \, \text{V}^{-1}\end{matrix}$

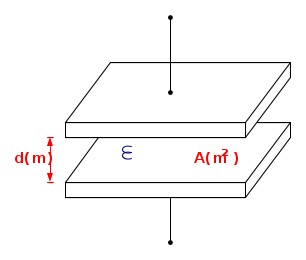
La capacità dipende dalla geometria delle armature e dalle proprietà fisiche dell'isolante interposto. Per il condensatore piano, costituito da due armature parallele distanti d e la cui superficie ha area A risulta:

$C=\varepsilon \frac{A}{d}$

con ε detta costante dielettrica assoluta dell'isolante, e si misura in farad diviso metro : $F m - 1$ Può essere vista come la capacità specifica dell'isolante (area e distanza delle armature unitaria). Per il vuoto (e l'aria) tale costante vale:

$\varepsilon_0=8{,}85\times 10^{-12}\; \text{F} \, \text{m}^{-1}$

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Quando la carica, quindi la tensione, varia, nel bipolo c'è una corrente che, come si può intuire, ha un'intensità tanto maggiore quanto più elevata è la rapidità di variazione della carica, quindi della tensione. Il verso della corrente inoltre è positivo se la carica aumenta, negativo se la carica diminuisce.
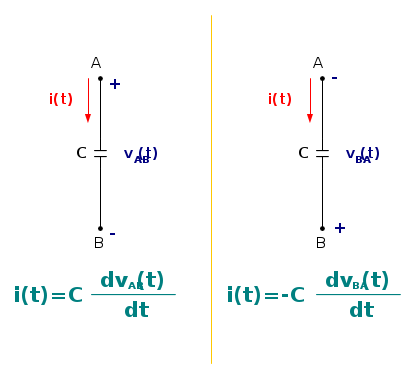
Risulta chiaro quindi che il condensatore è attraversato da una corrente solo nel momento in cui vi sia una variazione di potenziale ai capi dello stesso. C'è dunque un legame non tra i valori istantanei di tensione ed intensità, ma tra intensità e rapidità di variazione delle tensione. La rapidità di variazione della tensione è matematicamente rappresentata dalla sua derivata rispetto al tempo. In definitiva l'intensità istantanea nel condensatore è proporzionale alla derivata della tensione e la costante di proporzionalità è la capacità. Matematicamente, assumendo la convenzione di utilizzatore (quindi intensità positiva entrante nel polo assunto a potenziale maggiore, A nel nostro caso), si scrive così:

$i(t)=C\frac{\mathrm{d} v_{AB}(t)}{\mathrm{d} t}$

Breve nota di Analisi

Questa nota è un tentativo di esporre sinteticamente sia il concetto di derivata, apparso nella definizione precedente, che quello di integrale, che useremo successivamente, illustrandone il simbolismo matematico. E' ovviamente necessaria una trattazione più rigorosa per capire. Molto meglio perciò consultare un testo di Analisi Matematica magari partendo dai link seguenti:

Ad ogni modo chi non ha ancora acquisito tali concetti può provare a leggere queste poche righe.

Derivata

Se consideriano un piccolissimo intervallo di tempo, che indicheremo con

d t

, anche l'eventuale variazione di tensione sarà piccolissima e l'indicheremo con

d v (t)

. Tali piccolissime variazioni sono anche dette "infinitesimi" che è l'aggettivo matematico che indica una grandezza il cui valore tende a zero. Il rapporto tra una variazione di tensione ed il tempo in cui essa avviene rappresenta la rapidità di variazione media della tensione. Se l'intervallo di tempo è piccolissimo, il rapporto $v^\prime(t)=\text{d}v(t)/\text{d}t$ è chiamato derivata e rappresenta la rapidità di variazione istantanea della tensione.

Integrale

Se in un condensatore inizialmente carico in in certo istante

t 0

ad una tensione

v 0 = v (t 0)

fluisce una intensità di corrente, la sua tensione varia. Ad un istante t, successivo a

t 0

la tensione

v (t)

sarà uguale alla tensione iniziale più, algebricamente, la sua variazione. Suddividendo l'intervallo di tempo

t - t 0

in innumerevoli piccolissimi intervalli

dτ

, la variazione totale della tensione sarà la somma di tutte le piccole variazioni corrispondenti agli intervalli. Tale somma è chiamata integrale nell'intervallo considerato, ed è rappresentata matematicamente con una esse allungata alle cui estremità sono indicati gli estremi dell'intervallo. Si scrive allora

$v(t)=v(t_0)+\int_{t_0}^{t} \mathrm{d}v(\tau)$

Per la relazione tra intensità e corrente nel condensatore, si ha

$\text{d}v(t)=\frac{i(t)}{C}\text{d}t$

quindi

$v(t)=\frac{1}{C}\int_{t_0}^{t}i(\tau)\mathrm{d}\tau +v(t_0)$

L'integrale della intensità corrisponde ovviamente alla variazione della carica sul condensatore. All'istante finale t essa vale

$q(t)= \int_{t_0}^{t}i(\tau)\mathrm{d}\tau +Cv(t_0)$

Possiamo qui osservare che

$i(t)=\frac{\text{d}q(t)}{\text{d}t}$

il che "mostra" come "la derivata dell'integrale" sia la funzione integranda

i (t)

E' il teorema fondamentale del calcolo integrale per la cui definizione rigorosa occorre però riferirsi almeno al link

NB. La variabile indipendente della funzione integranda è, nel nostro caso, il tempo, e si è scelto di indicarla con

τ

per distinguerla dall'estremo superiore di integrazione

t

; può però essere di qualsiasi altro tipo.

Se dunque la variazione è nulla, è nulla la derivata, il che ci permette di affermare che la corrente nel condensatore è pure nulla. In continua, non abbiamo variazioni della tensione, e in tale regime il condensatore si comporta allora come un circuito aperto.
Riassumiamo la defizione negli schemi che seguono

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Potenza ed energia

A variazioni positive di carica corrispondono positive della tensione e viceversa.

Se allora si calcola la potenza entrante nel bipolo :

$p(t)=v(t) i(t)=v(t) C\frac{\mathrm{d} v(t)}{\mathrm{d} t}$

si osserva che ad essa può corrispondere una variazione di tensione, e quindi di corrente, sia positiva che negativa.
La potenza elettrica può dunque sia entrare che uscire dal bipolo.
Nel primo caso il condensatore accumula energia elettrica, nel secondo caso la restituisce. Nel primo caso si rinforza il campo elettrico (si vedrà il concetto nell'art. 9) presente nel condensatore, nel secondo si indebolisce. Il bilancio tra l'energia assorbita e quella ceduta nell'intervallo di tempo, agli estremi del quale il condensatore ha la stessa tensione, è sempre di parità: il condensatore non consuma energia elettrica ma la scambia solamente attraverso i morsetti.
Se vogliamo un'analogia, il condensatore può essere paragonato ad una bombola che contiene gas (la carica) sotto pressione (la tensione).

La tensione è la variabile di stato del condensatore e ne definisce l'energia elettrostatica immagazzinata: L'energia immagazzinata è uguale al lavoro che è stato fatto per caricare il condensatore. Infatti se consideriamo che il lavoro infinitesimo fatto per spostare una carica dq da una piastra all'altra, sotto la tensione V, vale:

$\mathrm{d}W=V\mathrm{d}q=\frac{q}{C}\mathrm{d}q$

l'integrale dell'equazione appena scritta è l'energia potenziale immagazzinata dal condensatore; gli estremi d'integrazione saranno la carica iniziale (supposta nulla) e la carica finale Q.

$W=\int_{0}^{Q}\frac{q}{C}\; \mathrm{d}q=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}CV^2$

Osservazione.L'inverso della capacità è denominato elastanza. Il condensatore può essere assimilato ad una molla che, deformata, immagazzina energia potenziale in proporzione al quadrato della deformazione. La costante di proporzionalità è il coefficiente di elasticità della molla. Nell'analogia dunque la deformazione della molla corrisponde alla carica del condensatore.

Approfondimenti sul condensatore

Esercizio
Appunti sul condensatore by mir
Il condensatore reale by posta10100
Due esercizi di elettrostatica by admin

Esercizio 1 Esercizio 2
Esercizio 3 Esercizio 4 Esercizio 5... e tanti altri se spulciate nel forum ;)

Il bipolo induttore

E' il bipolo accumulatore di energia elettrica sotto forma di energia magnetica che può essere considerata come l'"energia cinetica elettrica" essendo associata al movimento delle cariche. Ogni elemento circuitale percorso da corrente è un induttore in quanto crea un campo magnetico. Come realizzazione pratica l'induttore è, in generale, una bobina avvolta su un nucleo (che può essere anche aria). La "quantità di campo magnetico" è denominata flusso magnetico concatenato con l'induttore, la cui unità di misura è il weber, che a sua volta è volt per secondo :

$\begin{matrix}\text{Wb=V} \, \text{s}\end{matrix}$

Discuteremo questa grandezza nell'articolo finale del corso. Per ora ci basti sapere che è proporzionale all'intensità di corrente e la costante di proporzionalità si chiama coefficiente di autoinduzione o induttanza.
In parole povere quando un induttore è percorso da una corrente I, produce un campo magnetico, le cui linee di forza si concatenano con l'induttore stesso. Ciò significa che le linee magnetiche, che sono linee chiuse, attraversano le spire della bobina, quindi la bobina stessa. Spire e linee magnetiche stanno tra loro come gli anelli di una catena. Cerchiamo di spiegare meglio il concetto di flusso concatenato: indicando con Φ il flusso generato dall'induttore di N spire mentre è attraversato da una corrente I, ipotizzando che il flusso generato attraversi ogni spira, il flusso concatenato risulta:

$\begin{matrix}\phi _c=N\phi \end{matrix}$

Il rapporto tra flusso concatenato e corrente che lo ha generato, definisce l'induttanza:

$L=\frac{\phi _c}{I}$

L'unità di misura del coefficiente di autoinduzione si può ricavare dalla relazione impostata e si chiama henry, che equivale a ohm per secondo :

$\begin{matrix}\text{H=V} \, \text{s} \, \text{A}^{-1}=\Omega \, \text{s}\end{matrix}$

Se la corrente varia, ai capi dell'induttore si manifesta una tensione proporzionale alla velocità di variazione della corrente, che si oppone alla variazione stessa, e la costante di proporzionalità resta $L$ . Parleremo in seguito delle forze elettromotrici indotte; per il momento, come fatto per il condensatore, ci limitiamo a definire quella che è la variabile di stato per un induttore.
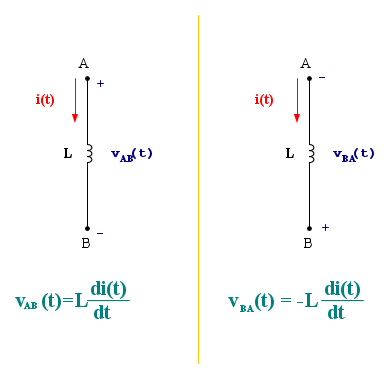
Assumendo la convenzione dell'utilizzatore, e considerando le grandezze elettriche variabili nel tempo, il legame tra la tensione e l'intensità di corrente è dato dall'espressione:

$v_{AB}(t)=L\frac{\mathrm{d} i(t)}{\mathrm{d} t}$

E' matematicamente identica all'espressione che lega corrente e tensione nel condensatore in cui però tensione ed intensità sono scambiate di posizione. Si può allora dire che l'induttanza è il rapporto tra tensione e rapidità di variazione della corrente.
Tutto ciò che si è detto per la tensione sul condensatore è valido per l'intensità di corrente nell'induttore. Se l'intensità di corrente, quindi il flusso magnetico, è costante, ai capi dell'induttore non c'è alcuna tensione.
Ciò porta a dire che l'induttore in corrente continua è un cortocircuito.
Se l'induttore è alimentato da un generatore di corrente, la tensione è immediatamente calcolabile; se invece è alimentato da un generatore di tensione, per calcolare l'intensità di corrente è necessario conoscere il valore che essa aveva all'istante iniziale, di applicazione del generatore: i(t₀). L'intensità di corrente è dunque la variabile che ne definisce lo stato.

Ripetendo le considerazioni fatte per il condensatore (riquadro "matematico"), la corrente ad un istante generico successivo a $t 0$ , vale

$i(t)=\frac{1}{L}\int_{t_0}^{t}v(\tau)\mathrm{d}\tau +i(t_0)$

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Potenza ed energia

Valutiamo ora in termini di potenza il comportamento dell'induttore:

$p(t)=v(t) i(t)=L\frac{\mathrm{d} i(t)}{\mathrm{d} t} i(t)$

dove la potenza risulta assorbita o generata a seconda del segno della variazione di corrente; come già detto l'analogia con il condensatore è forte, è come se si scambiassero le variabili di stato.
L'energia immagazzinata da un induttore percorso da una corrente continua I risulta:

$W=\int_{0}^{I}Li(t)\mathrm{d}i=\frac{1}{2}LI^2$

Osservazione. Poiché l'intensità è legata alla velocità di spostamento delle cariche, si può pensare ad una analogia tra l'induttanza L e la massa di un corpo per i moti traslatori (con il momento di inerzia nelle rotazioni), il che suggerisce di paragonare l'induttore ad un volano, l'organo meccanico che immagazzina energia cinetica. In tale analogia alla corrente elettrica corrisponde la velocità di traslazione (angolare nei moti rotatori), come mostra l'espressione dell'energia scritta.

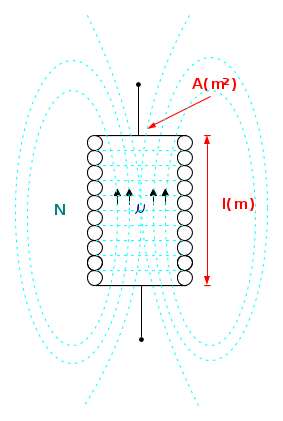
Il coefficiente di autoinduzione (o induttanza) è un parametro che contiene in sé le caratteristiche geometriche, le rotazioni complete della corrente, le proprietà fisiche del mezzo in cui si sviluppa il campo magnetico. Per fare un esempio, se consideriamo un avvolgimento di $N$ spire, di lunghezza media $l$ e sezione $A$ , l'espressione dell'induttanza assume la seguente forma:

$L=\mu N^2\frac{A}{l}$

con $μ$ permeabilità magnetica assoluta del mezzo in cui si propaga il campo magnetico. Per il vuoto e per l'aria tale costante vale:

$\mu _0=4\pi \times 10^{-7}\; \; \text{H/m}$

La formula per l'induttanza del solenoide lineare è approssimata, e vale solo per solenoidi la cui lunghezza è molto maggiore del diametro.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Ritorneremo su queste grandezze quando affronteremo con maggiori dettagli lo studio del campo magnetico (art. 10)

Approfondimenti sull'induttore

Esercizio
L'induttore by mir
Energia del campo magnetico by admin

Esercizio 1, Esercizio 2, Esercizio 3, Esercizio 4

Conclusioni

I bipoli descritti sono sufficienti per rappresentare tutti i fenomeni energetici di un qualsiasi circuito elettrico od elettronico comunque complesso.
L'analisi dei circuiti sarà sviluppata nei prossimi articoli; qui vogliamo riassumere il ruolo svolto dai bipoli esaminati nei circuiti.
Generatori ed utilizzatori sono le sorgenti ed i pozzi dell'universo elettromagnetico.
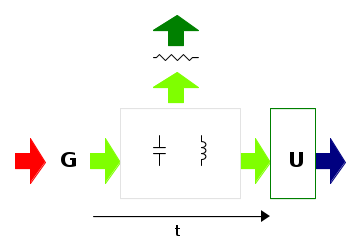
Il campo elettromagnetico, come una cinghia che trasferisce energia meccanica tra due pulegge, trasferisce l'energia che entra dalle sue sorgenti ai pozzi che la richiedono, regolando il trasferimento per mezzo degli accumulatori interni: il condensatore e l'induttore che esistono unicamente nell'universo elettromagnetico.
Il pozzo sempre presente, affamato di energia cui inesorabilmente toglie parte della capacità di trasformarsi, è la resistenza che rappresenta il cosmico effetto termico cui, tramite il concetto di entropia, è legata la freccia del tempo:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Estratto da "https://www.electroyou.it/mediawiki/index.php?title=UsersPages:Lillo:bipoli"

Commenti e note

Inserisci un commento

di Massi79, 12 anni fa

Complimenti per l'articolo, è perfetto.

Rispondi

di attilio, 12 anni fa

Ottima esposizione, bravo Lillo!

Rispondi

di Guerra, 12 anni fa

Ottimo articolo e soprattutto molto utile. Bravo lillo :)

Rispondi

di lillo, 12 anni fa

grazie ancora ragazzi :) mir, comincia a delinearsi la tua immagine nella mia mente :)

Rispondi

di mir, 12 anni fa

Ottimo,complimenti lillo .. anche se non utilizzo il phone, mi è piaciuta l'apertura..grazie . ;)

Rispondi

di DarwinNE, 12 anni fa

Bravissimo!

Rispondi

di clavicordo, 12 anni fa

Mi unisco ai complimenti, soprattutto per la chiarezza espositiva e la concatenazione logica degli argomenti!

Rispondi

di MassimoB, 12 anni fa

Davvero complimenti

Rispondi

di carlomariamanenti, 12 anni fa

lillo, U did a great job! Thanks, -carlo.

Rispondi

di matteo375, 12 anni fa

Bravissimo :)

Rispondi

di lillo, 12 anni fa

Errata corrige by RenzoDF: il coefficiente di temperatura dipende dalla temperatura di riferimento. L'espressione della permeabilità è 4π*10^(-7) H/m e non 4*10^(-7) H/m.

Rispondi

di Lelettrico, 12 anni fa

Ottimo articolo davvero, a tratti anche suggestivo ...

Rispondi

di lillo, 12 anni fa

Grazie davvero a tutti ragazzi (e ragazze ;)). errata corrige su segnalazione di Lelettrico: la resistività del ferro è circa 0,096 Ω*mm²/m e non 0,019 Ω*mm²/m.

Rispondi