Prefazione
Non molto tempo fa trovandomi a studiare matematica per gli esami di analisi dopo anni dalle scuole superiori una delle tante difficoltà che ho incontrato per prime è stata il ripasso di trigonometria, così ho pensato di condividere una serie di appunti che potrebbero essere utili a chi come me si trova o si troverà ad affrontare tali studi o semplicemente ha voglia di rinfrescare la memoria sugli argomenti che tratterò.
Il radiante
Prima di tutto definiamo cosa è un radiante, unità di misura che ci accompagnerà a lungo negli studi.
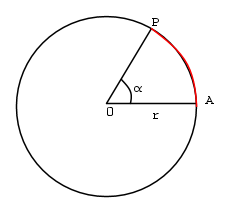
Un radiante è definito come la misura dell' angolo al centro  quando l' arco AP ha una lunghezza pari al raggio r della circonferenza.
quando l' arco AP ha una lunghezza pari al raggio r della circonferenza.
Da cui si deduce che un angolo di 360° sottende un arco pari a 2πr
Per convertire gradi in radianti basta utilizzare la seguente proporzione:
g:r = 180:π
Dove g è l' angolo in gradi ed r l' angolo in radianti
Se abbiamo un angolo in gradi e vogliamo convertirlo in radianti avremo:

Se abbiamo un angolo in radianti e vogliamo convertirlo in gradi avremo:

Di seguito ho riportato la tabella di conversione di alcuni angoli ricorrenti
| Angoli in gradi | Angoli in radianti |
|---|---|
| 0° | 0 |
| 15° | 
|
| 30° | 
|
| 45° | 
|
| 60° | 
|
| 90° | 
|
| 180° | π |
| 270° | 
|
| 360° | 2π |
La circonferenza trigonometrica
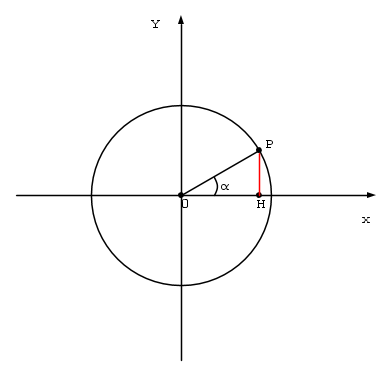
Consideriamo ora una circonferenze di raggio unitario e centro nell' orgine degli assi X e Y, tale circonferenza viene chiamata Circonferenza trigonometrica.
Consideriamo ora un punto P posizionato su di essa
Proiettiamo il punto P sull' asse delle ascisse e lo chiamiamo H.
Il segmento  rappresenta il coseno dell' angolo
rappresenta il coseno dell' angolo 
Il segmento  rappresenta il seno dell' angolo
rappresenta il seno dell' angolo 
Notiamo anche che il punto P sulla circonferenza ha coordinate P(cosα,sinα)
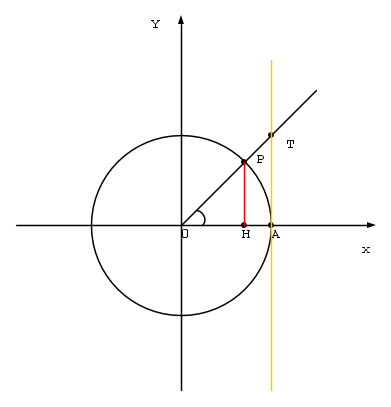
A questo punto introduciamo il concetto di tangente e cotangente
Il segmento  rappresenta La tangente dell' angolo
rappresenta La tangente dell' angolo 
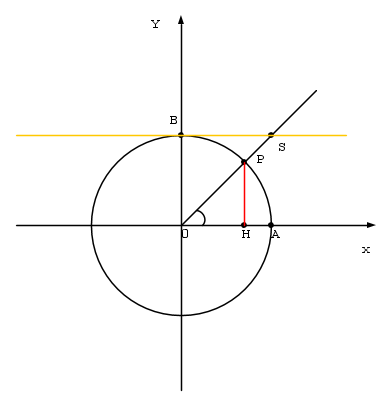
Il segmento  rappresenta La cotangente dell' angolo
rappresenta La cotangente dell' angolo 


Tangente
Cotangente
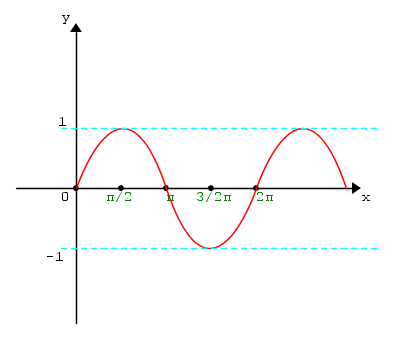
La funzione seno
f(x) = sinx
La funzione seno è periodica di periodo 2π
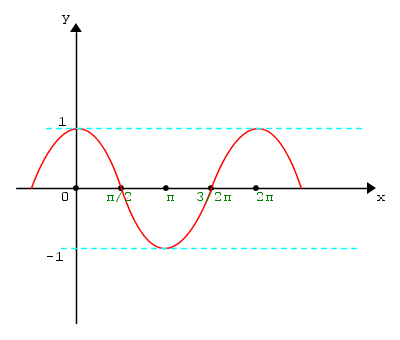
La funzione coseno
f(x) = cosx
La funzione coseno è periodica di periodo 2π
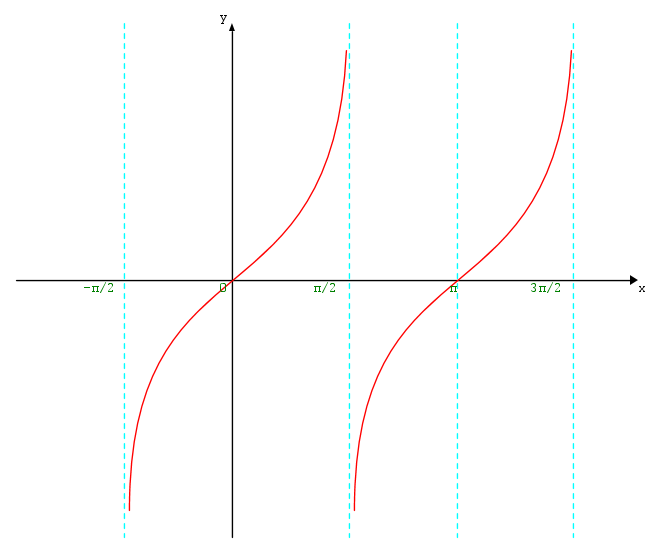
La funzione tangente
f(x) = tanx
La funzione tangente è periodica di periodo π
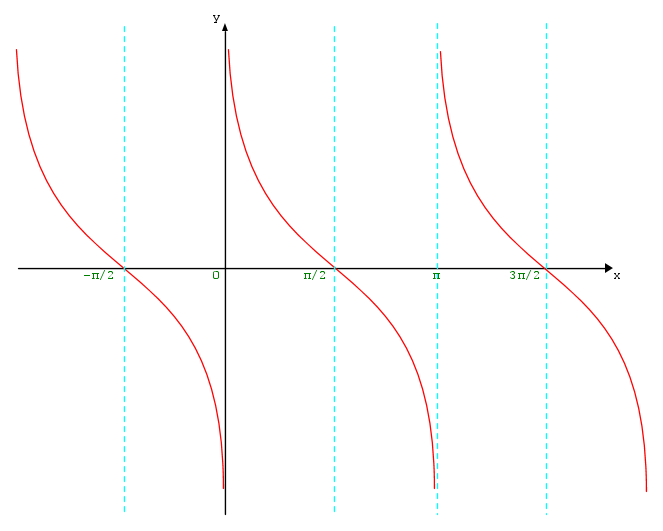
La funzione cotangente
f(x) = cotx
La funzione cotangente è periodica di periodo π
Gli archi associati
π - α
sin(π − α) = sinα
cos(π − α) = − cosα
tan(π − α) = − tanα
cot(π − α) = − cotα
π + α
sin(π + α) = − sinα
cos(π + α) = − cosα
tan(π + α) = tanα
cot(π + α) = cotα
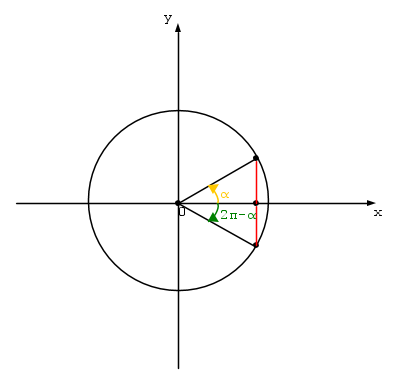
2π - α
sin(2π − α) = − sinα
cos(2π − α) = cosα
tan(2π − α) = − tanα
cot(2π − α) = − cotα
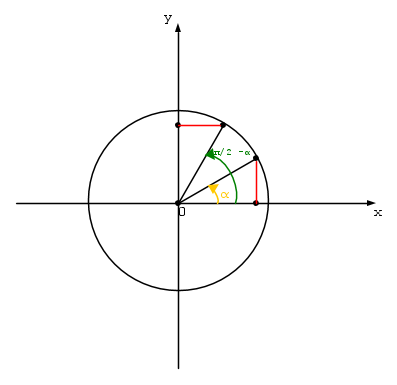
π/2 - α




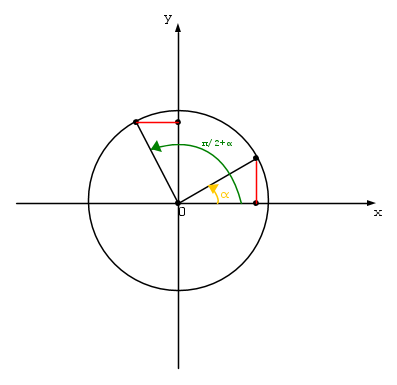
π/2 + α




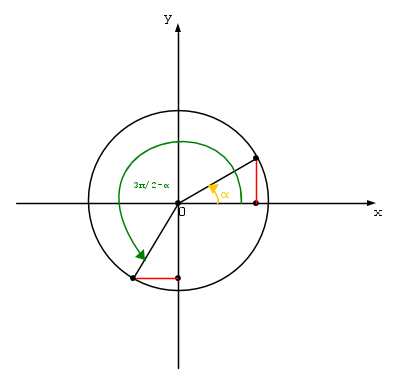
3π/2 - α




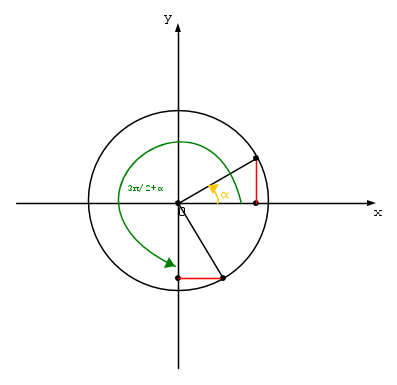
3π/2 + α




Angoli ricorrenti
| Angoli in gradi | Angoli in radianti | Seno | Coseno | Tangente | Cotangente |
|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | 
|
| 15° |  |  | 
|  | 
|
| 30° |  |  |  |  | 
|
| 45° |  |  |  | 1 | 1 |
| 60° |  |  |  |  |
|
| 90° |  | 1 | 0 |  | 0 |
| 180° | π | 0 | − 1 | 0 | 
|
| 270° |  | − 1 | 0 |  | 0 |
| 360° | 2π | 0 | 1 | 0 | 
|
Un pò di formule
Prima relazione fondamentale
sin2α + cos2α = 1
Formule di addizione
seno della somma
sin(α + β) = sinαcosβ + cosαsinβ
seno della differenza
sin(α − β) = sinαcosβ − cosαsinβ
coseno della somma
cos(α + β) = cosαcosβ − sinαsinβ
coseno della differenza
cos(α − β) = cosαcosβ + sinαsinβ
tangente della somma

tangente della differenza

Formule di duplicazione
seno del doppio dell' angolo
sin(2α) = 2sinαcosα
coseno del doppio dell' angolo
cos(2α) = cos2α − sin2α
tangente del doppio dell' angolo

Formule di bisezione
seno della metà di un angolo

coseno della metà di un angolo

tangente della metà di un angolo

Formule Parametriche
Posto

formula parametrica del seno

formula parametrica del coseno

formula parametrica della tangente

Formule di prostaferesi
somma di seni

differenza di seni

somma di coseni

differenza di coseni

Formule di werner



Bibliografia
Matematica di base di Giacomo Tommei Edizioni Apogeo
Matematica per i precorsi di Giovanni malafarina Edizioni McGraw-Hill
Istituzioni Di Matematiche di Giuseppe Zwirner Edizioni Cedam
Analitica e trigonometria di Giuseppe Zwirner Edizioni Cedam
Matematica generale di Romano Isler Edizioni Goliardiche
Manuale di metodi matematici di Allevi,Bertocchi,Birolini,Carcano,Gnudi,Moreni Edizioni Giappichelli
PreCalculus di Marco Bramanti Edizioni Esculapio
Elementi di matematica - Questioni fondamentali di Giorgio Giorgi Edizioni Giappichelli

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)