Cos'è ElectroYou | Login Iscriviti

ElectroYou - la comunità dei professionisti del mondo elettrico

18
voti

Esercizi random di Elettrotecnica

Indice

Premessa

Un discreto numero di utenti di Electroyou è costituito da studenti, i quali spesso chiedono aiuto per la risoluzione di esercizi. Generalmente sono svolti nel forum, preferibilmente con una interazione didattica tra l'esperto o gli esperti disponibili e lo studente.
Pensavo, tempo fa, quando mi illudevo ancora che questo sito fosse apprezzato per il suo intento formativo, di raccoglierli ed organizzarli in modo da poter essere parte di un testo di Elettrotecnica di base, generato proprio dalla mia attività internettiana.
Poi le cose vanno diversamente da come si sogna, sia perché l'impresa presenta obiettive difficoltà, sia perché intervengono fattori esterni che rallentano, se non fermano, lo sviluppo del sito, sia perché molti legami instauratisi si sfaldano e c'è sempre chi arriva ad insegnarti cosa fare e come farlo, liquefacendo la passione originaria, ma fondamentalmente perché manca la determinazione necessaria, e probabilmente anche la capacità per portarla a termine.
Beh, insomma, tutta la pappardella iniziale vuol essere una premessa (magari con un messaggio subliminale) per giustificare il titolo di questo articolo in cui riporto alcuni degli esercizi raccolti dal forum.

Es. 1

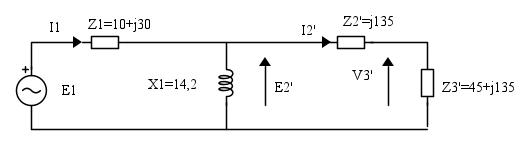
Nel circuito di figura calcolare le correnti nei rami.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad


Con Millman

\begin{array}{l} {\bar E_1} = {\rm{j}}10 \, \rm{V}\\ {\bar E_2} = 10 \, \rm{V} \\ R = 5 \, \Omega\\ {\dot Z_L} = {\rm{j}}5 \, \Omega\\ {\dot Z_C} = - {\rm{j}}5 \, \Omega\\ {\bar V_{AB}} = \frac{{\frac{{{\bar E_1}}}{R} + \frac{{{\bar E_2}}}{{{\dot Z_C}}}}}{{\frac{1}{R} + \frac{1}{{{\dot Z_L}}} + \frac{1}{{{\dot Z_C}}}}} = \frac{{\frac{{{\rm{j}}10}}{5} + \frac{{10}}{{ - {\rm{j}}5}}}}{{\frac{1}{5} + \frac{1}{{{\rm{j}}5}} + \frac{1}{{ - {\rm{j}}5}}}} = {\rm{j}}20 \, \rm{V}\\ {\bar I_3} = \frac{{{\rm{j}}20}}{{{\rm{j}}5}} = 4 \, \rm{A}\\ {\bar I_1} = \frac{{{\bar E_1} - {\bar V_{AB}}}}{R} = \frac{{{\rm{j}}10 - {\rm{j}}20}}{5} = - {\rm{j2}} \, \rm{A}\\ {\bar I_2} = {\bar I_3} - {\bar I_1} = 4 + {\rm{j2}} \, \rm{A} \end{array}


Con sovrapposizione degli effetti

Solo E1

\begin{array}{l} {\bar V_R} = \frac{{({\bar E_1} \cdot {\dot Z_R})}}{{({\dot Z_R} + \frac{{({\dot Z_L} \cdot {\dot Z_C})}}{{({\dot Z_L} + {\dot Z_C})}})}} = \frac{{({\bar E_1} \cdot {\dot Z_R}) \cdot ({Z_L} + {\dot Z_c})}}{{({\dot Z_R} \cdot ({\dot Z_L} + {\dot Z_C}) + ({\dot Z_L} \cdot {\dot Z_C}))}} = \\ =\frac{{({\bar E_1} \cdot {\dot Z_R}) \cdot 0}}{{({\dot Z_R} \cdot 0 + ({\dot Z_L} \cdot {\dot Z_C}))}} = 0 \, \rm{V}\\ {\bar I_{1}'} = \frac{{{\bar V_R}}}{R} = 0A\\ {\bar E_1} - R \cdot {\bar I_R} - {\bar V_L} = {\bar E_1} - {\bar V_L} = 0\\ {\bar V_L} = {\rm{j}}10 \, \rm{V}\\ {\bar V_C} = - {\bar V_L}\\ {\bar I_{3}'} = \frac{{{\bar V_L}}}{{{\dot Z_L}}} = 2 \, \rm{A}\\ {\bar I_{2}'} = \frac{{{\bar V_C}}}{{{\dot Z_L}}} = - 2 \, \rm{A} \end{array}

Solo E2

\begin{array}{l} \bar V_c = \frac{{({\bar E_2} \cdot {Z_C})}}{{({Z_C} + \frac{{({Z_R} \cdot {Z_L})}}{{({Z_R} + {Z_L})}}}} = \frac{{({\bar E_2} \cdot {Z_C}) \cdot ({Z_R} + {Z_L})}}{{({Z_C} \cdot ({Z_R} + {Z_L}) + ({Z_R} \cdot {Z_L}))}})\\ = \frac{{(10 \cdot - \rm{j}5) \cdot (5 + \rm{j}5)}}{{( - \rm{j}5 \cdot (5 + j5) + (5 \cdot j5))}} = \frac{{ - \rm{j}250 + 250}}{{25}} = 10 - \rm{j}10 \, \rm{V} \\ \\ {\bar E_2} - {\bar V_C} - {\bar V_L} = 0 \, \rm{V}\\ {\bar V_L} = {\bar E_2} - {\bar V_C}{\rm{ }} = {\rm{ }}10 - 10 + \rm{j}10{\rm{ }} = {\rm{ j}}10 \, \rm{V}\\ {\bar V_R} = - {\bar V_L}\\ {\bar I_{3}''} = \frac{{{\bar V_L}}}{{{Z_L}}} = \frac{{{\rm{j}}10}}{{{\rm{j5}}}} = 2 \, \rm{A}\\ {\bar I_{1}''} = \frac{{{\bar V_R}}}{R} = \frac{{ - {\rm{j}}10}}{5} = - {\rm{j2 \, A}}\\ \\ {\bar I_1} = {\bar I_{1}''} + {\bar I_{1}'} = - {\rm{j2 \, A}} \end{array}
\bar I_3=\bar I_3'+\bar I_3''=2+2=4 \, \rm{A}

Es. 2

Determinare l'indicazione del wattmetro

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

{I_C} = \frac{{{S_C}}}{{\sqrt 3 V}} = \frac{{\sqrt {{P^2} + {Q^2}} }}{{\sqrt 3 V}} = \frac{{\sqrt {{{1000}^2} + {{500}^2}} }}{{\sqrt 3 \times 1000}} = 0{,}646 \, {\rm{A}}

{P_R} = 3RI_C^2 = 3 \times 400 \times {\left( {0,646} \right)^2} = 500 \, {\rm{W}}
Indicando con VL la tensione concatenata ai capi della stella di induttanze {V_L} = \frac{{{S_L}}}{{\sqrt 3 {I_C}}} = \frac{{\sqrt {{{\left( {P + {P_R}} \right)}^2} + {Q^2}} }}{{\sqrt 3 {I_C}}} = \frac{{\sqrt {{{1500}^2} + {{500}^2}} }}{{\sqrt 3 \times 0{,}646}} = 1413 \, {\rm{V}}
La corrente nelle induttanze vale

{I_L} = \frac{{{V_L}}}{{\sqrt 3 {X_L}}} = \frac{{1413}}{{\sqrt 3 \times 100}} = 8{,}15 \, {\rm{A}}

Per l'indicazione del wattmetro occorre calcolare la corrente nella induttanza e lo sfasamento tra il fasore concatenata \bar V_{31} ed il fasore \bar I_{2L}
La corrente detta ritarda di 90 gradi rispetto alla tensione di fase 2 la quale ritarda di 90 gradi rispetto alla tensione \bar V_{31}

Nel calcolo si è scelta la fase zero il fasore \bar E_{1L} e si è considerata diretta la terna delle tensioni
\begin{array}{l} {{\bar E}_{1L}} = \frac{{1413}}{{\sqrt 3 }}\angle 0 = 815\angle 0{\rm{V}}\\ {{\bar E}_{3L}} = \frac{{1413}}{{\sqrt 3 }}\angle 120 = 815\angle 120 = - 407 + {\rm{j}}706{\rm{V}}\\ {{\bar V}_{31L}} = {{\bar E}_{3L}} - {{\bar E}_{1L}} = -815 - 407 + {\rm{j}}706 = -1222 + {\rm{j}}706 = 1411\angle 150{\rm{V}}\\ {{\bar I}_{2L}} = \frac{{{{\bar E}_{2L}}}}{{{\rm{j}}{X_L}}} = \frac{{815\angle - 120}}{{100\angle 90}} = 8{,}15\angle - 210\\ \angle {{\bar V}_{31}}{{\bar I}_{2L}} = 150 + 210 = 360\\ W = {V_L}{I_L}\cos360 = 1413 \times 8{,}15 \times 1= 11516{\rm{W}} \end{array}

Grafico fasoriale

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Es. 3

Topic di origine

Determibare la tensione Vx

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Nel precedente procedimento è stato utilizzato il metodo della falsa posizione che consiste nello scegliere un valore arbitrario ma opportuno per la grandezza cercata (tensione o corrente), che è l'effetto prodotto dal generatore, risalendo quindi al valore del generatore che l'avrebbe prodotto. Si calcola quindi il rapporto tra il valore cosi' trovato e quello dell'effettivo generatore presente. Per tale rapporto vanno moltiplicati i valori di tutte le altre grandezze del circuito in cui si era scelto arbitrariamente il valore della grandezza cercata. Nel caso specifico si è scelto V_x= 4 \, \rm{V} trovando che il generatore di corrente agente dovrebbe avere in tal caso una corrente di 10 A. Il generatore effettivo ha però una corrente di 6 A per cui il valore di Vx che con la scelta arbitraria era di 2 V, varrà V_x=2 \times \frac{10}{6}= \frac{10}{3} \, \rm{V}

Es. 4

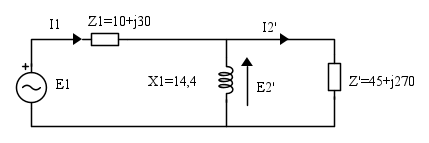
Nel seguente circuito determinare

  1. i_1(t), \, i_2(t), \, e_2(t), \, v_3(t)
  2. potenza attiva e reattiva del generatore
  3. potenza attiva e reattiva totale delle impedenze \dot Z_1, \dot Z_2, \dot Z_3

Il trasformatore non ha perdite di alcun tipo, né flussi dispersi

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Metodo che utilizza il circuito equivalente del trasformatore

la riluttanza del circuito magnetico del trasformatore è


\Re = \frac{{4l}}{{\mu S}} = \frac{{4 \times 15 \times {{10}^{ - 2}}}}{{4\pi {{10}^{ - 7}} \times 600 \times 16 \times {{10}^{ - 4}}}} = 4{,}97 \times {10^5} \, {{\rm{H}}^{ - 1}}

l'induttanza del primario è perciò
{L_1} = \frac{{N_1^2}}{\Re } = \frac{{{{150}^2}}}{{4{,}97 \times {{10}^5}}} = 0{,}0453 \, {\rm{H}}
la corrispondente reattanza è

{X_1} = \omega {L_1} = 314 \times 0{,}0453 = 14{,}2 \, \Omega

Il trasformatore, non avendo nessun tipo di perdite, è ideale ed il circuito può essere allora così rappresentato

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

si ha il rapporto di trasformazione

m=\frac{N_1}{N_2}=\frac{150}{50}=3
Le impedenze al secondario possono essere trasportate al primario moltiplicando per il quadrato del rapporto di trasformazione, ricavando il circuito

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad


Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad


\begin{array}{l} \dot Z' = {{\dot Z}_2}' + {{\dot Z}_3}' = 45 + {\rm{j}}270 \, \Omega \\ {{\dot Z}_p} = \frac{{\dot Z'{\rm{j}}{X_1}}}{{\dot Z' + {\rm{j}}{X_1}}} = \frac{{14{,}2\angle 90 \times 274\angle 80,5}}{{288\angle 81}} = 13,5\angle 89{,}5) = 0,116 + j13,5 \, \Omega \\ {{\dot Z}_{eq}} = {{\dot Z}_p} + {{\dot Z}_1} = 10{,}1 + {\rm{j}}43{,}5 \, \Omega \end{array}


\begin{array}{l} {{\bar E}_1} = 230\angle 60^\circ {\rm{V}}\\ {{\bar I}_1} = \frac{{{{\bar E}_1}}}{{{{\dot Z}_{eq}}}} = \frac{{230\angle 60^\circ }}{{10,1 + {\rm{j}}43,5}} = \frac{{230\angle 60^\circ }}{{44,7\angle 76{,}9^\circ }} = 5{,}14\angle - 17^\circ {\rm{A}} \end{array}

{i_1}(t) = \sqrt 2 \cdot 5{,}13\sin \left( {314t - \frac{{17\pi }}{{180}}} \right)

\begin{array}{l} {{\bar E}_2}' = {{\bar E}_1} - {{\dot Z}_1}{{\bar I}_1} = 115 + {\rm{j}}199 - \left( {10 + {\rm{j}}30} \right) \times 5{,}14\angle - 17 = \\ = 115 + {\rm{j}}199 - 31{,}6\angle 71{,}6 \times 5{,}14\angle - 17 = \\ =115 + {\rm{j}}199 - 94 - {\rm{j}}132 = 21 + {\rm{j}}67= 70{,}2 \angle 72{,}6 \,{\rm{V}} \end{array}
{e_2}(t) = 23{,}4 \times \sqrt 2 \sin \left( {314t + \frac{{72,6\pi }}{{180}}} \right)


\begin{array}{l} {{\bar E}_2} = \frac{{{{\bar E}_2}'}}{m}\\ = 7 + \rm{j}22{,}3 = 23,4\angle + 72{,}6 \, \rm{V} \end{array}


\begin{array}{l} {{\bar I}_2}' = \frac{{{{\bar E}_2}'}}{{\dot Z'}} = \frac{{21 + {\rm{j}}67}}{{45 + {\rm{j}}270}} = \frac{{70{,}2\angle + 72{,}6}}{{274\angle 80{,}5}} = 0{,}256\angle - 7{,}9\\ {{\bar I}_2} = m{{\bar I}_2}' = 0{,}768\angle - 7{,}9 \, \rm{A}\\ {i_2}(t) = 0{,}768 \times \sqrt 2 \sin \left( 314t - \frac{\pi 7{,}9}{180} \right )\, \rm{A} \end{array}


\begin{array}{l} {{\bar V}_3} = {{\dot Z}_3}{{\bar I}_2} = \left( {5 + {\rm{j}}15} \right) \times 0,768\angle - 7,9 = 15,8\angle 71,5 \times 0,75\angle - 7,9 = \\ = 12{,}1\angle 63{,}6 \, {\rm{V}}\\ {v_3}(t) = 12{,}1 \sqrt 2 \sin \left( 314t - \frac{\pi 63,6}{180} \right ) \, {\rm{V}} \end{array}

Le potenze richieste

Calcoleremo le potenze complesse dove la parte reale è la potenza attiva mentre quella immaginaria è la reattiva

\begin{array}{l} \dot S = {{\bar E}_1} \cdot {{\hat I}_1} = 230\angle 60 \times 5{,}13\angle 17 = 1180\angle 77 = 265 + {\rm{j}}1150 \, {\rm{VA}}\\ \\ {{\dot S}_{{{\dot Z}_1}}} = {{\dot Z}_1}I_1^2 = \left( {10 + {\rm{j}}30} \right) \times {5{,}13^2} = 263 + {\rm{j789 \, VA}}\\ {{\dot S}_{{{\dot Z}_2}}} = {{\dot Z}_2}I_2^2 = {\rm{j}}15 \times {0{,}768^2} = {\rm{j8{,}85VA}}\\ {{\dot S}_{{{\dot Z}_3}}} = {{\dot Z}_3}I_2^2 = \left( {5 + {\rm{j}}15} \right) \times {0{,}768^2} = 2{,}95 + {\rm{j8{,}85 \, VA}} \end{array}

Altro metodo

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Con riferimento al precedente circuito in cui sono rappresentate le reattanze di auto e mutua induzione, si possono scrivere le equazioni

\left\{ \begin{array}{l} \left( {{\rm{j}}{X_1} + {{\dot Z}_1}} \right){{\bar I}_1} + {\rm{j}}{X_M}{{\bar I}_2} = {{\bar E}_1}\\ {\rm{j}}{X_M}{{\bar I}_1} + \left( {{\rm{j}}{X_2} + {{\dot Z}_2} + {{\dot Z}_3}} \right){{\bar I}_2} = 0 \end{array} \right.

dove si ha

\begin{array}{l} {L_1} = \frac{{N_1^2}}{\Re } = \frac{{{{150}^2}}}{{4,97 \times {{10}^5}}} = 0{,}0453 \, {\rm{H}}\\ {L_2} = \frac{{N_2^2}}{\Re } = \frac{{{{50}^2}}}{{4,97 \times {{10}^5}}} = 0,5 \times {10^{ - 2}}{\rm{H}}\\ {X_2} =\omega {L_2}=314 \times 0,5 \times {10^{ - 2}} = 1,58\Omega \\ {X_1} = \omega {L_1} = 314 \times 0,0453 = 14{,}2\Omega \\ M =\frac{{{N_1}{N_2}}}{\Re } = \frac{{150 \times 50}}{{4,97 \times {{10}^5}}} = 1,51 \times {10^{ - 2}}{\rm{H}}\\ {X_M} = \omega M = 314 \times 1,51 \times {10^{ - 2}} = 4,74\Omega \end{array}
Quindi
\left\{ \begin{array}{l} \left( {{\rm{j}}14,4 + 10 + {\rm{j}}30} \right){{\bar I}_1} + {\rm{j}}4,74{{\bar I}_2} = 230\angle 60\\ {\rm{j}}4,74{{\bar I}_1} + \left( {{\rm{j}}1,57 + {\rm{j}}15 + 5 + {\rm{j}}{{15}_3}} \right){{\bar I}_2} = 0 \end{array} \right.

\left\{ \begin{array}{l} \left( {10 + {\rm{j}}44,4} \right){{\bar I}_1} + {\rm{j}}4,74{{\bar I}_2} = 230\angle 60\\ {\rm{j}}4,74{{\bar I}_1} + \left( {5 + {\rm{j}}31,6} \right){{\bar I}_2} = 0 \end{array} \right.


\begin{array}{l} \Delta = \left| {\begin{array}{*{20}{c}} {10 + {\rm{j}}44,4}&{{\rm{j}}4,74}\\ {{\rm{j}}4,74}&{5 + {\rm{j}}31,6} \end{array}} \right| = 50 + {\rm{j}}316 + {\rm{j}}222 - 1403 + 22,5 = \\ = - 1330 + {\rm{j}}538 = 1434\angle 158 \end{array}

\begin{array}{l} {\Delta _{{I_1}}} = \left| {\begin{array}{*{20}{c}} {230\angle 60}&{{\rm{j}}4,74}\\ 0&{5 + {\rm{j}}31,6} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {230\angle 60}&{{\rm{j}}4,74}\\ 0&{32\angle 81} \end{array}} \right| = \\ = 7360\angle 141 \end{array}

{{\bar I}_1} = \frac{{{\Delta _{{I_1}}}}}{\Delta } = \frac{{7360\angle 141}}{{1434\angle 158}} = 5,13\angle - 17 \, \rm{V}

{\Delta _{{I_2}}} = \left| {\begin{array}{*{20}{c}} {10 + {\rm{j}}44,4}&{230\angle 60}\\ {{\rm{j}}4,74}&0 \end{array}} \right| = - 1090\angle 150


{{\bar I}_2} = \frac{{{\Delta _{{I_2}}}}}{\Delta } = \frac{{ - 1090\angle 150}}{{1434\angle 158}} = 0,76\angle - 8 \, {\rm{A}}

Es. 5

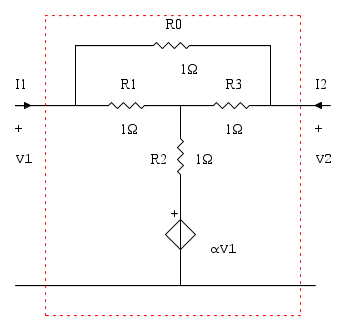
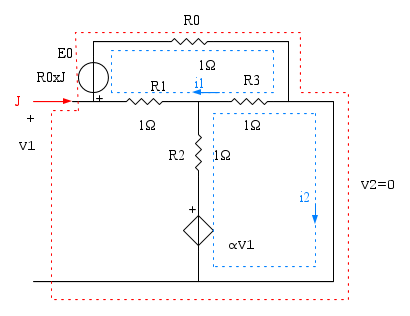
Dato il doppio bipolo di figura, calcolare la matrice delle conduttanze.
NB: i terminali uscenti dal rettangolo tratteggiato sono le due porte del bipolo, la 1 a sinistra, la 2 a destra.
Convenzionalmente si considerano positive le correnti che entrano dal terminale assunto a potenziale più alto, cioè quello contrassegnato con il "+"

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

\left\{ \begin{array}{l}{I_1} = {G_{11}}{V_1} + {G_{12}}{V_2}\\{I_2} = {G_{21}}{V_1} + {G_{22}}{V_2}\end{array} \right.

Calcolo di {G_{11}} = {\left| {\frac{{{I_1}}}{{{V_1}}}} \right|_{{V_2} = 0}}

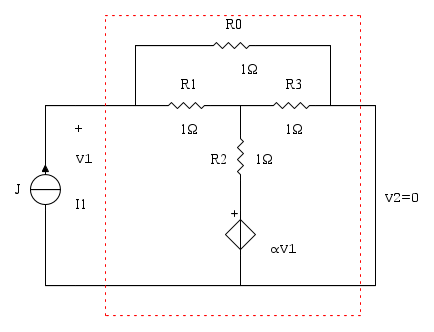
Si cortocircuita la porta 2, si impone una corrente alla porta 1 con un generatore di corrente (J = I1) entrante dal terminale assunto a potenziale più alto, si calcola la tensione alla porta 1 cioè ai capi del generatore ideale di corrente imposto. (Oppure si impone la tensione V1 e si calcola la corrente I1)

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad


Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad


\left\{ \begin{array}{l}\left( {{R_0} + {R_1} + {R_3}} \right){i_1} - {R_3}{i_2} = - {R_0}J\\ - {R_3}{i_1} + \left( {{R_2} + {R_3}} \right){i_2} = \alpha {V_1}\\{V_1} = {R_0}\left( {J + {i_1}} \right)\end{array} \right.
\left\{ \begin{array}{l}\left( {{R_0} + {R_1} + {R_3}} \right){i_1} - {R_3}{i_2} = - {R_0}J\\ - {R_3}{i_1} + \left( {{R_2} + {R_3}} \right){i_2} = \alpha {R_0}\left( {J + {i_1}} \right)\end{array} \right.
\left\{ \begin{array}{l} 3{i_1} - {i_2} = - J\\ - {i_1}\left( {1 + \alpha } \right) + 2{i_2} = \alpha J \end{array} \right.
\Delta = \left| {\begin{array}{*{20}{c}} 3&{ - 1}\\ { - 1 - \alpha }&2 \end{array}} \right| = 5 - \alpha
{\Delta _{{i_1}}} = \left| {\begin{array}{*{20}{c}} { - J}&{ - 1}\\ {\alpha J}&2 \end{array}} \right| = J\left( {\alpha - 2} \right)

{i_1} = \frac{{{\Delta _{{i_1}}}}}{\Delta } = \frac{{J\left( {\alpha - 2} \right)}}{{5 - \alpha }}

{V_1} = J + \frac{{J\left( {\alpha - 2} \right)}}{{5 - \alpha }} = \frac{{3J}}{{5 - \alpha }}

{G_{11}} = \frac{J}{{{V_1}}} = \frac{{5 - \alpha }}{3} \, \text{S}

Calcolo di \quad {G_{12}} = {\left| {\frac{{{I_1}}}{{{V_2}}}} \right|_{{V_1} = 0}}

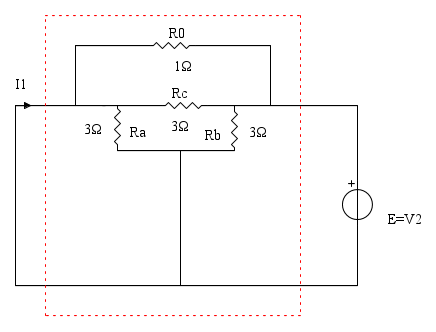
Si cortocircuita la porta 1 (V1 = 0), si impone la tensione alla porta 2 con un generatore ideale di tensione (V2 = E), si calcola la corrente I1

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Trasformiamo la stella nel triangolo equivalente

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Ra è cortocircuitata mentre R0 è in parallelo ad Rc

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

{I_1} = - \frac{E}{{{R_{0c}}}} = - \frac{4}{3}E

{G_{12}} = \frac{{{I_1}}}{{{V_2}}} = - \frac{4}{3} \, \text{S}

Calcolo {G_{21}} = {\left| {\frac{{{I_2}}}{{{V_1}}}} \right|_{{V_2} = 0}}

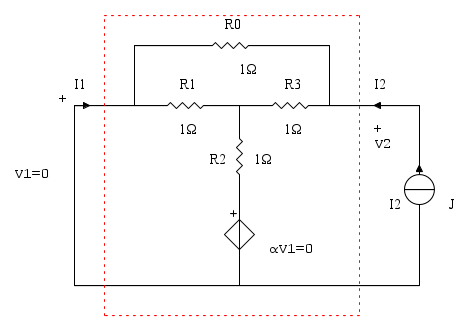
Si cortocircuita la porta 2 (V2 = 0) , si impone una tensione alla porta 1 (V1 = E), si calcola la corrente I2 entrante sempre dal terminale assunto a potenziale più alto (+)

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

\left\{ \begin{array}{l} \left( {{R_1} + {R_2}} \right){i_1} - {R_2}{i_2} - {R_1}{i_3} = E\left( {1 - \alpha } \right)\\ - {R_2}{i_1} + \left( {{R_3} + {R_2}} \right){i_2} - {R_3}{i_3} = \alpha E\\ - {R_1}{i_1} - {R_3}{i_2} + \left( {{R_1} + {R_0} + {R_3}} \right) = 0 \end{array} \right.
\begin{array}{l} \Delta = \left| {\begin{array}{*{20}{c}} 2&{ - 1}&{ - 1}\\ { - 1}&2&{ - 1}\\ { - 1}&{ - 1}&3 \end{array}} \right| = 2\left| {\begin{array}{*{20}{c}} 2&{ - 1}\\ { - 1}&3 \end{array}} \right| + \left| {\begin{array}{*{20}{c}} { - 1}&{ - 1}\\ { - 1}&3 \end{array}} \right| - \left| {\begin{array}{*{20}{c}} { - 1}&2\\ { - 1}&{ - 1} \end{array}} \right| = \\ = 2 \times \left( {6 - 1} \right) - 3 - 1 - \left( {1 + 2} \right) = 3 \end{array}
\begin{array}{l} {\Delta _{{i_2}}} = \left| {\begin{array}{*{20}{c}} 2&{E\left( {1 - \alpha } \right)}&{ - 1}\\ { - 1}&{\alpha E}&{ - 1}\\ { - 1}&0&3 \end{array}} \right| = - E\left( {1 - \alpha } \right)\left| {\begin{array}{*{20}{c}} { - 1}&{ - 1}\\ { - 1}&3 \end{array}} \right| + \alpha E\left| {\begin{array}{*{20}{c}} 2&{ - 1}\\ { - 1}&3 \end{array}} \right| = \\ = - E\left( {1 - \alpha } \right)\left( { - 3 - 1} \right) - 4E + \alpha E\left( {6 - 1} \right) = 4E - 4E\alpha - 4E + 5E\alpha = E\alpha \end{array}
\begin{array}{l} {i_2} = \frac{{{\Delta _{{i_2}}}}}{\Delta } = \frac{{E\alpha }}{3}\\ {I_2} = - {i_2} = - \frac{{E\alpha }}{3} \end{array}

{G_{21}} = \frac{{{I_2}}}{E} = - \frac{\alpha }{3}


Calcolo di {G_{22}} = {\left| {\frac{{{I_2}}}{{{V_2}}}} \right|_{{V_1} = 0}}

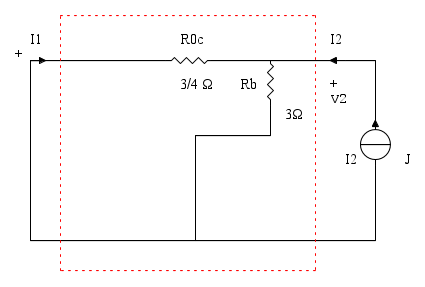
Si cortocircuita la porta 1, V1 = 0, si impone la corrente I2 con un generatore di corrente (I2 = J), si calcola la tensione V2, cioè ai capi del generatore di corrente

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

{V_2} = J\frac{{{R_{0c}}{R_b}}}{{{R_{0c}} + {R_b}}} = J\frac{{\frac{3}{4} \times 3}}{{\frac{3}{4} + 3}} = J\frac{9}{{15}} = J\frac{3}{5}

{G_{22}} = \frac{J}{{{V_2}}} = \frac{5}{3} \, {\rm{S}}

Estratto da "https://www.electroyou.it/mediawiki/index.php?title=UsersPages:Admin:esercizi-random"
12

Commenti e note

Inserisci un commento

di ,

Ogni tanto mi dimentico di manifestare la mia soddisfazione per commenti lusinghieri. Poi ci ricapito per caso su, dopo un anno, come in questo caso, ed allora devo proprio ricordarmi di farlo! Quindi:
Pietro, il tuo commento è come l'ossigeno per questa attività-gioco! ;-)
Riccardo, le tue considerazioni su ciò che può dare un insegnante, anche da una tastiera, dopo aver usato il gesso, sono corroboranti, perché sottolineano il lato umano che è alla base anche della trasmissione di cultura tecnica.
Massimo il tuo riconoscimento di un valore didattico in quanto spargo nel web, conoscendo bene la tua competenza elettrica, è per me molto importante. :-)
Marc96, Edmond, richiurci, folgore98: grazie anche a voi! :-)

Rispondi

di ,

Questo forum è un ottimo ambiente, per me unico, in cui trovare risposte serie e professionali. Insegno da parecchio tempo e con nessun collega riesco a dialogare come con voi, anzi in genere non si dialoga di aspetti tecnici. Spero possiate continuare. Grazie

Rispondi

di ,

Ma sai, caro Zeno, che mi hai fatto sorridere, con la frase: "mi era parso, tempo fa, di essere riuscito a realizzare qualcosa di originale con questo sito". E' davvero modesta. Tu sei riuscito IN PIENO a realizzare qualcosa di originale con questo sito. E' vero che i social hanno portato via una buona fetta di utenti dai forum, però io non ragionerei in termini di quantità, ma di qualità. Il sito deve certo sopravvivere, quindi il numero di iscritti conta, ma la attenzione che tu metti nel fare passare argomenti tecnici e non è innegabile da parte di chiunque. Ammetto di non capire chi si iscriva per denigrare. Se io volessi denigrare questo sito non mi ci iscriverei di sicuro, ma cercherei di fare di meglio altrove, in modo che questo sito ne soffra di reputazione. In fondo però, se guardiamo il peggio finiremo per guardare in un baratro. Cerchiamo di essere noi il sito migliore. Per quanto riguarda i miei contributi, mah, non mi sono mai reputato particolarmente capace, anche all'università. Ero curioso, questo sì, ma nulla di più. Ho conosciuto tanta gente molto più in gamba di me, che meritava il mio posto più di me... Il mistero è casomai come io abbia fatto a conservarlo fino alla fine, quel posto! Se è vero che ho dato qualche contributo non è grazie a me, ma alla comunità, a questo sito, alla "brancata" di gente megaipercompetente che questo sito è stato in grado di raccogliere (tu in primis), alle opportunità che mi hai dato tu e Nicolò mettendo in piedi tutto questo. Per questo nutro molto rispetto per il sito e molta stima per tutti i professionisti (e molti di loro sono diventati anche miei amici) che frequentano questo forum. EY continua a splendere, forse la sua luce ti risulta un po' offuscata dai molti che hanno cercato e cercano di affossarlo, ma questo è solo un problema tuo, si tratta solo di prendere lo straccetto e lucidarsi gli occhiali, per vedere nuovamente cosa sia davvero e non cosa ti appaia. Con stima.

Rispondi

di ,

Pietro, mi ero dimenticato di rispondere al tuo commento, su cui ora sono per caso ritornato.
Devo dire sinceramente che sì, mi era parso, tempo fa, di essere riuscito a realizzare qualcosa di originale con questo sito, ma, progressivamente, la mia sensazione è diventata quella di non aver fatto niente di speciale.
C'è chi, come te, lo ha apprezzato, vi ha contribuito e continua a farlo, con la sua qualità tecnica ed umana, qualità che non dipende da me e che avrebbe comunque trovato uno spazio per manifestarsi.
Altri invece, come sai bene, sono arrivati a disprezzare l'ambiente ed il suo animatore, un atteggiamento, a dire il vero, che mi è parso esagerato, indice di problemi forse più loro che miei, ma che io non ho saputo evitare o controllare bene, rendendo questo spazio uguale a tanti altri.
Avrei desiderato vederlo crescere, ma non ho capito come si doveva fare. Così si è assestato al livello di galleggiamento attuale. Spero che continui ad essere utile per merito di chi è rimasto fedele e delle nuove leve.

Rispondi

di ,

Decisamente ottimo ed utile a chiunque! Grazie! :D

Rispondi

di ,

Gli articoli di Zeno sono un punto fermo salutare per contrastare il mare di sciocchezze che si leggono in rete . Ad esempio facebook con i suoi gruppi tematici alla "elettricisti che passione" ha causato danni incalcolabili alla divulgazione della cultura elettrica. Gli articoli di Zeno sono indispensabili. Scritti del genere in rete non si trovano. Salvare e conservarli è indispensabile

Rispondi

di ,

E' sempre un onore essere citato in un articolo di Zeno, sia perché lo stimo tanto come persona, quanto come Elettrotecnico. Una particolarità della premessa è che chi l'ha scritta non si è accorto di aver comunque raggiunto gli obiettivi che si prefiggeva: il libro di cui parla ha le sue pagine scritte nei numerosi articoli del blog e il dialogo costruttivo fra docente ed allievo è tutto nel forum. Le difficoltà ci sono sempre e, se proprio dobbiamo cercare qualcosa da dirgli, possiamo solo dirgli che pecca di umiltà. Ti sei accorto, Zeno, di cosa hai costruito con EY?

Rispondi

di ,

E allora io ringrazio, anche se questo articolo non mi "serve" direttamente. Ho letto comunque con piacere l'introduzione, anche se amara, perchè è l'ennesima conferma della passione che ci metti. Certe vicende non accadono solo su EY, purtroppo è uno degli effetti del web e dell'ondata di populismo e dilettantismo che dilaga

Rispondi

di ,

grazie

Rispondi

di ,

Insegnare dovrebbe essere (purtroppo uso il condizionale) una missione, una professione ritenuta fondamentale per chiunque. Lo si può fare anche da una tastiera dopo averlo fatto per molti anni da dietro una cattedra con le mani sporche di gesso, i molti insuccessi, ma anche i molti successi anche silenti. Perchè molti nel silenzio dello sguardo incrociando il loro prof delle superiori pensano: ecco il mio professore di ... Molti salutano a distanza di anni, molti altri pensano di essere stati dimenticati. Ben vengano questi articoli Zeno; perchè riempiano di cultura la rete, troppo piena ahimè di sciocchezze. In molti lo leggeranno; forse pochi ti ringrazieranno nonostante molti ne abbiano usufruito, ma è un mestiere e passione spesso ingrata. D'altronde anche il contadino semina a piene mani.

Rispondi

di ,

Appena potro', lo leggero' con calma. Grazie admin!

Rispondi

Inserisci un commento

Per inserire commenti è necessario iscriversi ad ElectroYou. Se sei già iscritto, effettua il login.