Indice |
Generalità
La caratteristica fondamentale del cortocircuito di induttanze pure, è stata evidenziata in questo post di IsidoroKZ. Qui sono raccolti alcuni esercizi presi da richieste pervenute nel forum.
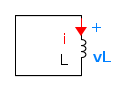
Quando si cortocircuita un'induttanza pura si ottiene la maglia del disegno sottostante e la soluzione dell'equazione che ne regola il funzionamento è una costante i = K, il cui valore dipende dalla condizione iniziale, cioè dalla corrente che percorre l'induttanza nel momento del cortocircuito.
La corrente rimane confinata con quel valore nell'induttanza indefinitamente. L'energia magnetica dunque rimane inalterata.
L'induttanza in pratica scompare dal circuito, cioè non interagisce con esso, né al nuovo regime permanente, né durante il transitorio. Essa trattiene per sé tutta l'energia iniziale e l'assestamento delle energie riguarda gli altri bipoli accumulatori.
Quindi, ad esempio, se l'induttanza cortocircuitata è l'unica presente in un circuito con resistenze e condensatori, il circuito si comporta come un sistema del primo ordine. Nel ramo che la cortocircuita, alla corrente esistente all'istante iniziale nell'induttanza si somma la corrente impressa dal resto del circuito.

iL = costante = iL(0 − )
Es.1
- Un generatore ideale di corrente alternata sinusoidale alimenta la serie R,L in cui l'induttanza all'istante zero è cortocircuitata.
Con il tasto aperto il circuito è una semplice serie RL. Trattandosi di un generatore ideale di corrente, le grandezze da calcolare sono le tensioni.
Con il tasto chiuso la corrente nella resistenza rimane identica a quella del generatore; nell'induttore circolerà la corrente che il generatore eroga nell'istante del corto. Cambiano ovviamente le tensioni in quanto ora il circuito è costituito da una semplice resistenza: l'induttore "scompare" dal circuito elettrico.

Es. 2
- generatore ideale di tensione alternata che alimenta la serie RL in cui all'istante zero l'induttanza viene cortocircuitata

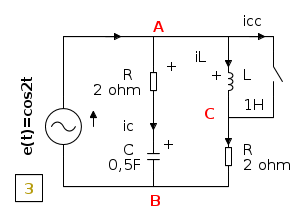
Es. 3
- Al circuito 2 è stato aggiunto un ramo RC in parallelo al ramo RL.
Essendo il generatore di tensione ideale, la tensione ai sui capi non subisce variazioni alla chiusura del tasto.
Per quel che riguarda il ramo di destra tutto avviene come nel precedente esercizio e, nel ramo centrale, non si ha alcuna variazione: il regime sinusoidale per t>0 è identico a quello per t<0.
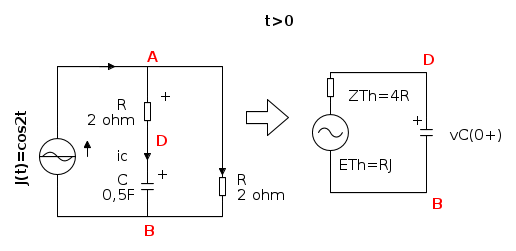
Es.4
- Ora al posto del generatore ideale di tensione c'è un generatore ideale di corrente.
In questo caso il cortocircuito dell'induttanza determina una variazione nel regime delle correnti nei due rami in parallelo per la diversa ripartizione della corrente mantenuta costante dal generatore ideale. La variazione di corrente nel ramo del condensatore, provoca una variazione della sua tensione, quindi dell'energia complessivamente immagazzinata nel circuito. L'energia magnetica mantiene costante il valore che ha nell'istante in cui viene cortocircuitata.

All'istante t=0 l'induttanza è cortocircuitata e in pratica "scompare" dal circuito da considerare per t>0. Si può ricavare il generatore equivalente visto dai terminali del condensatore per trovare l'andamento della tensione su di esso, tenendo presente che all'istante t=0 il condensatore è carico alla tensione vC(0 − )




Grafici
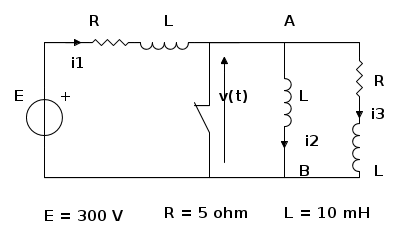
Es.5
- Nel seguente circuito, avviene l'inverso: inizialmente l'induttanza centrale è cortocircuitata ed il circuito è a regime in quelle condizioni. Dobbiamo ipotizzare che la corrente sia nulla perché, teoricamente, potrebbe anche esserci, qualsiasi corrente continua, che circola nell'induttanza stessa e nel cortocircuito, a seconda di come si è arrivati nella condizioni di circuito chiuso.
Qui tutto è più complicato. Io allora me la cavo rimandando al thread del forum dove l'esercizio è stato ampiamente discusso.
Segnalo le considerazioni sul calcolo delle condizioni iniziali, in particolare a partire dal post di RenzoDF e le varie soluzioni preparate in in formato pdf da Dimaios.
Buona lettura! ;)

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)