ElectroYou - la comunità dei professionisti del mondo elettrico

Vai a: navigazione, ricerca

Questo articolo è una riedizione di un vecchio articolo riveduto, corretto (si spera) ed ampliato con gli strumenti del blog: formule matematiche in LaTeX e schemi in FidoCadJ. L'antica idea era di scrivere una trattazione tradizionale sulle macchine sincrone, possibilmente abbastanza completa. Poi dell'idea ci si dimentica; del resto non c'è nessuno che richiede di portarla avanti ed il web è già pieno di trattazioni di questo tipo. Ora i disegni di mir in FidoCadJ sulla macchina sincrona, me l'hanno fatta ricordare, per cui ho pensato ad una riedizione.

Indice

1 Come funziona un generatore sincrono
2 Tensione indotta a vuoto in un conduttore di statore
- 2.1 Avvolgimento
  - 2.1.1 Fattore di avvolgimento
  - 2.1.2 Fattore di accorciamento
- 2.2 Armoniche
3 Avvolgimenti trifasi
4 Caratteristica a vuoto
- 4.1 Esercizio
5 Bibliografia

Come funziona un generatore sincrono

Il rotore della macchina è un elettromagnete cilindrico, liscio o con espansioni polari, che produce un'induzione con un'alternanza di poli Nord e Sud pari al numero delle espansioni, lungo la circonferenza di traferro. Le prime due figure dell'articolo di mir, mostrano due sezioni trasversali di macchine sincrone a poli salienti, quadripolare la prima, bipolare la seconda.

Il traferro è la corona cilindrica in aria che separa lo statore dal rotore. Ponendo in rotazione il rotore con un motore primo (es: turbina a vapore o idraulica), gli avvolgimenti situati nelle cave della periferia interna di statore, sono sede, per la legge di Faraday-Lenz, di una tensione indotta. In generale l'induzione non è perfettamente sinusoidale, ma può essere scomposta, secondo Fourier, in una fondamentale e nelle sue armoniche. La frequenza della tensione indotta dalla fondamentale, è proporzionale alla velocità di rotazione del rotore ed al numero di poli del campo induttore ( le semionde positive e negative della fondamentale dell'induzione); il suo valore efficace è proporzionale al flusso magnetico polare prodotto dalla fondamentale dell'induzione, alla frequenza, al numero di conduttori che compongono l'avvolgimento. Analogo discorso vale per le armoniche dell'induzione, che danno luogo a distribuzioni sinusoidali dell'induzione con un numero di semionde multiplo del numero di poli, che inducono tensioni di frequenza ugualmente multiple della fondamentale.
Per semplicità ci si riferirà sempre alla fondamentale, salvo riferimenti espliciti alle armoniche.
Generalmente si tratta di macchine trifasi, quindi dotate di tre avvolgimenti identici collegati a stella od a triangolo.
Quando si chiudono gli avvolgimenti su carico, circolano in essi correnti che producono un nuovo campo magnetico, detto reazione di indotto. Nelle macchine trifasi tale campo ruota con la stessa velocità del rotore ed ha lo stesso numero di poli. Si ha perciò una nuova configurazione dell'induzione al traferro, una nuova onda sinusoidale che ruota alla stessa velocità del rotore e di ampiezza che può differire da quella a vuoto sia in diminuzione che in aumento.
Generalmente si ha diminuzione dell'ampiezza dell'induzione e di conseguenza del flusso polare e della tensione indotta con carichi ohmico induttivi, un aumento con impedenze ohmico capacitive. Il carico induttivo, che costituisce il comune carico elettrico industriale, ha dunque un effetto smagnetizzante, magnetizzante quello capacitivo, effetti maggiori quanto più elevata è la loro componente reattiva.
La tensione effettiva sul carico differisce pertanto da quella a vuoto. Oltre alla variazione della tensione indotta dovuta alla variazione del flusso magnetico provocata dalla reazione di indotto, c'è anche quella dovuta alle cadute di tensione ohmiche ed induttive, dovute alla resistenza ed alle reattanze di dispersione dell'avvolgimento stesso.
Il problema che si deve dunque risolvere nel funzionamento a carico della macchina sincrona è quello di mantenere la tensione desiderata sul carico.
Ciò si può ottenere intervenendo sulla corrente di eccitazione, aumentandola adeguatamente in caso di carichi ohmico-induttivi e diminuendola in caso di carichi ohmico-capacitivi.
La componente resistiva del carico, richiede alla macchina l'erogazione di potenza attiva. Il campo magnetico di reazione in tal caso produce una coppia frenante sul rotore. Il motore primo deve allora equilibrare questa coppia resistente producendo una coppia motrice. Ciò avviene mediante trasformazione dell'energia primaria che alimenta il motore primo.
Un appropriato sistema di regolazione provvede a mantenere costante la velocità di rotazione del rotore, quindi la frequenza delle tensioni prodotte.
Se il carico è puramente reattivo, la reazione di indotto è in opposizione di fase ( induttivo) o in fase (capacitivo) con il campo di induttore, determinando smagnetizzazione o magnetizzazione rispettivamente, senza dar luogo a coppie frenanti, quindi senza determinare una ulteriore richiesta di energia al motore primo.

Tensione indotta a vuoto in un conduttore di statore

Consideriamo una porzione di una macchina con rotore a poli sporgenti, rettificandola.

L'andamento dell'induzione al traferro prodotta dagli avvolgimenti di eccitazione con $N e$ spire per polo, percorse dalla corrente continua $I e$ , (induzione assunta positiva quando uscente dal rotore), può essere ottenuto dalle seguenti considerazioni.
Per un tubo di flusso di sezione $S x = l Δ x$ con $Δ x$ intervallo molto piccolo che contiene l'ascissa x, ed $l$ lunghezza assiale della macchina, per la legge di Hopkinson si può scrivere

$\Phi_x=\frac{2N_eI_e}{\Re}$

$B(x)=\frac{\Phi_x}{S_x}$

Dove $\Re$ è la riluttanza magnetica totale del tubo di flusso. Alla riluttanza contribuiscono sia l'aria (traferro: tratti di linea scuri) che il ferro (tratti di linea chiari); quindi

$\Re=\Re_{aria}+\Re_{Ferro}$

Trascurando la riluttanza del ferro rispetto quella dell'aria, si può osservare che $B (x)$ dipende in pratica dalla lunghezza del tratto in aria. Sagomando opportunamente la superficie superiore del polo (scarpa polare) si può ottenere un andamento sinusoidale:
${\Re _a} = \frac{{{l_a}\left( x \right)}}{{{\mu _0}{S_x}}} \to B\left( x \right) = \frac{{2{N_e}{I_e}}}{{\frac{{{l_a}\left( x \right)}}{{{\mu _0}{S_x}}}{S_x}}} = \frac{k}{{{l_a}\left( x \right)}} \to \frac{1}{{{l_a}\left( x \right)}} = \frac{1}{{{l_{a,\min }}}}\sin \left( {\frac{x}{\tau }\pi } \right)$
La corrente di eccitazione è costante, quindi lo è pure l'induzione rispetto al sistema di riferimento solidale con il rotore. Ponendo in rotazione il rotore a $n$ giri/min, la sinusoide che descrive l'induzione magnetica al traferro, ruota essendo fissa rispetto al rotore.

La velocità relativa tra un qualsiasi conduttore di statore ed il campo magnetico solidale con il rotore, corrisponde alla velocità periferica di un punto della circonferenza al traferro che circoscrive il rotore e vale

$v=\frac{n}{60} 2 p \tau$

Dove $τ$ è la lunghezza di un polo misurata lungo detta circonferenza, cioè il semipasso polare, $p$ è il numero di coppie polari, $n$ il numero di giri al minuto.
In ciascun conduttore di statore nasce allora una fem data da

e = B l v

dove $l$ è la lunghezza assiale del conduttore, $v$ la velocità detta, e $B$ l'induzione magnetica cui il conduttore è soggetto. Tale induzione non è, per il conduttore di statore, costante nel tempo in quanto diverso è in ogni istante il punto della circonferenza esterna di rotore che si trova di fronte ad un conduttore. In pratica un conduttore di statore vede passare di fronte a sé un'onda sinusoidale di induzione, alla velocità $v$ .
La distanza temporale tra due massimi positivi di induzione è

$T=\frac{2 \tau}{v}=\frac{60}{np}$

La $B$ che investe il conduttore di statore varia dunque con legge sinusoidale nel tempo data da

$B(t)=B_M \sin \left ( \frac{2 \pi}{T} t \right )$

la cui frequenza è

$f= \frac{1}{T}=\frac{np}{60}$

La forza elettromotrice indotta in ogni conduttore è pertanto sinusoidale, e le forze elettromotrici di conduttori che stanno in cave adiacenti di statore sono elettricamente sfasate di in angolo $α$ che, indicando con $n c$ il numero totale di cave, vale

$\alpha=p \alpha_{mecc}=p \frac{2 \pi}{n_c}$

Generalmente gli avvolgimenti di statore sono tre (macchine trifasi) e si fornisce un parametro $q$ che indica il numero di cave per polo e per fase. Si ha pertanto $n_c=3 \times 2pq=6pq$ da cui

$\alpha_{mecc}=\frac{\pi}{3pq}$

$\alpha=p \alpha_{mecc}=\frac{\pi}{3q}$

Il valore efficace della fem indotta in ogni conduttore vale

$E=k_f E_{medio}=k_f \frac {2}{\pi} E_M$

$E_M=B_M l 2p \tau \frac {n}{60}$

quindi

$E=k_f \frac{2}{\pi} B_M l 2p \tau \frac{n}{60}=k_f B_{medio} l \tau \frac{2pn}{60}=2k_f f \Phi$

dove

$Φ = B m e d i o l τ$ (flusso polare)

$f=\frac{pn}{60}$ (frequenza)

e se consideriamo l'onda di induzione perfettamente sinusoidale $(k f = 1,11)$

$E=2{,}22\,f\,\Phi$

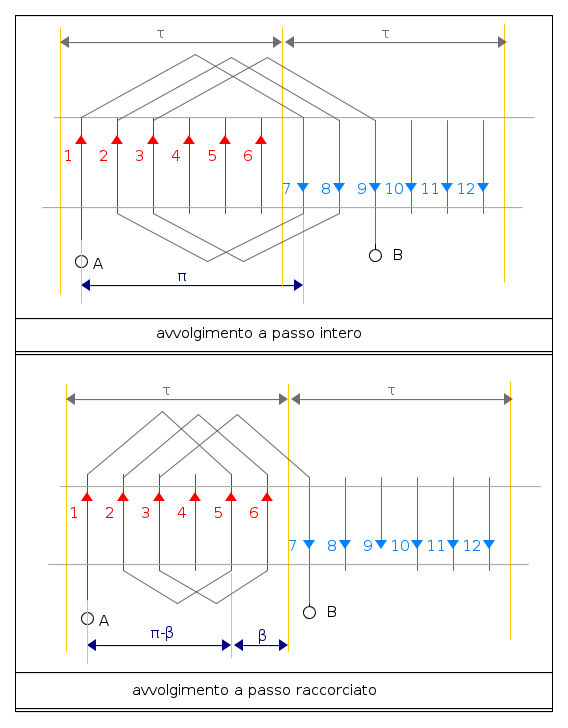
Avvolgimento

Un avvolgimento è costituito dalla serie di più conduttori posti in cave diverse. La tensione ai suoi capi non corrisponde alla somma aritmetica dei valori efficaci delle tensioni dei singoli conduttori, ma alla somma geometrica. E' a passo intero, quando i conduttori di una cava sono collegati con i conduttori della cava che dista esattamente la lunghezza di un polo, o a passo raccorciato se distano meno di un semipasso.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il numero dei conduttori che compongono l'avvolgimento è dato da $N = 2 p q n i$ dove n_i è il numero dei conduttori presenti in una cava facenti parte dell'avvolgimento e la tensione ai capi dell'avvolgimento è data da

$E=2k_f \, k_i \, k_r \, N \, f \, \Phi$

dove $k i$ è denominato fattore di avvolgimento e rappresenta il rapporto tra la la somma geometrica e la somma aritmetica delle tensioni dei conduttori che appartengono allo stesso polo, mentre $k r$ è denominato fattore di accorciamento, e rappresenta il rapporto tra la tensione effettivamente ottenuta con il passo raccorciato e la massima che si sarebbe ottenuta a passo intero

NB per l'andamento sinusoidale dell'induzione si ha

$E=2,{,}22 k_i \, k_r \, N \, f \, \Phi$

Fattore di avvolgimento

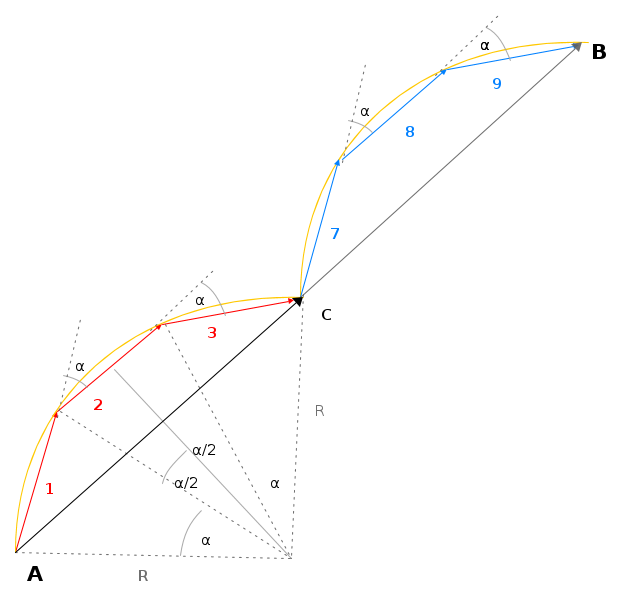
Tacciamo il diagramma vettoriale delle tensioni dei conduttori di un avvolgimento a passo intero. Si suppone per semplicità un conduttore per cava e si usano 3 conduttori per polo (q=3). Il valore efficace della tensione di ogni conduttore vale $E$ , come mostrato in precedenza ; $α$ è l'angolo elettrico di sfasamento tra le tensioni di conduttori in cave adiacenti. I conduttori che distano un semipasso polare sono collegati in modo che le loro tensioni siano in fase. La tensione della serie dei conduttori 1, 2, 3 ha lo stesso valore ed è in fase a quella della serie dei conduttori 7,8,9.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

AC e CB rappresentano le tensioni parziali delle due serie di conduttori e sono uguali in modulo ed in fase; la loro somma AB corrisponde alla tensione ai capi dell'avvolgimento. AC è il doppio della corda della circonferenza di raggio R. L'angolo al centro vale $q α$ . Si ha allora:

$R = \frac{ \frac E 2}{{\sin \left( {\frac{\alpha }{2}} \right)}}$
$AB = 2AC=2 \times 2 \cdot R\sin \left( {\frac{{qa}}{2}} \right) = 2E\frac{{\sin \left( {\frac{{qa}}{2}} \right)}}{{\sin \left( {\frac{\alpha }{2}} \right)}}$

${k_i} = \frac{{AB}}{{2qE}} = \frac{{2E\frac{{\sin \left( {\frac{{qa}}{2}} \right)}}{{\sin \left( {\frac{\alpha }{2}} \right)}}}}{{2qE}} = \frac{{\sin \left( {\frac{{qa}}{2}} \right)}}{{q\sin \left( {\frac{\alpha }{2}} \right)}}$

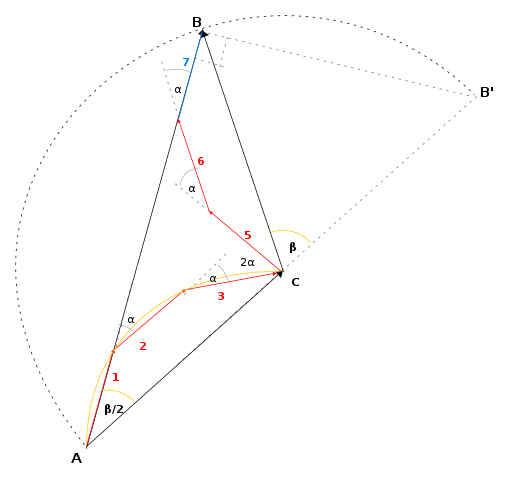
Fattore di accorciamento

Se la seconda serie di conduttori dista meno di un semipasso polare dalla precedente, si ha, come già detto, un avvolgimento a passo raccorciato. Nella figura che segue la seconda serie è costituita dai conduttori delle cave 5,6,7 come nello schema d'avvolgimento già tracciato. La loro somma geometrica ha modulo sempre uguale a quella dei conduttori 7,8,9 del collegamento a passo intero, ma, rispetto a questa, risulta ruotata in senso antiorario dell'angolo $β$ che è l'angolo elettrico di raccorciamento rispetto al passo intero, ed è un multiplo di $α$ .

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Si ha ora
$AB = AB'\cos \left( {\frac{\beta }{2}} \right)$
$A B'$ è la tensione dell'avvolgimento a passo intero. Il fattore di accorciamento vale perciò
$k_r=\cos \left( {\frac{\beta }{2}} \right)$

Armoniche

Se l'andamento dell'induzione al traferro non è perfettamente sinusoidale occorre, come detto, considerare le armoniche della scomposizione secondo Fourier. Le considerazioni precedenti rimangono praticamente inalterate. Si deve solo considerare che la frequenza di ogni armonica è multipla della fondamentale e che l'angolo elettrico è, come già scritto del resto, l'angolo meccanico moltiplicato per il numero di coppie polari, cioè di semionde dell'armonica considerata. La tensione indotta corrispondete all'armonica $ν$ è dunque

$E_{\nu}=2{,}22\,k_{i\nu} \, k_{r \nu}f{\nu}\,\Phi_{\nu}N$

con
$Φ ν$ flusso polare corrispondente all'armonica

${k_{i\nu }} = \frac{{\sin \left( {\nu \frac{{q\alpha }}{2}} \right)}}{{q\sin \nu \frac{\alpha }{2}}}$

${k_{r\nu }} = \cos \left( {\nu \frac{\beta }{2}} \right)$

L'adozione di un opportuno passo raccorciato può ridurre considerevolmente il fattore di raccorciamento di determinate armoniche contribuendo quindi a perfezionare la forma d'onda della tensione.

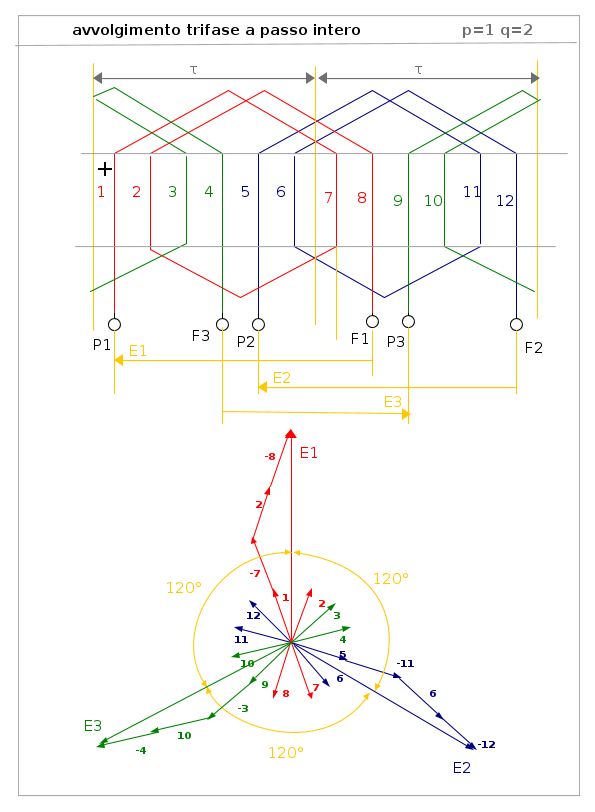
Avvolgimenti trifasi

Sono costituiti da tre avvolgimenti che occupano, ciascuno, un terzo dei conduttori di statore. Le tensioni a vuoto risultanti sono sfasate tra loro di 120° elettrici. I tre acvvolgimenti possono essere collegati a stella od a triangolo.

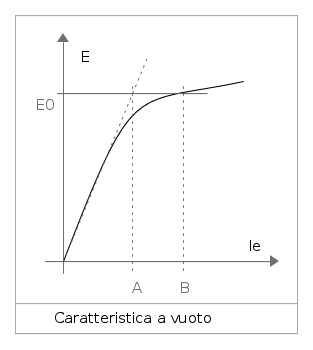
Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Caratteristica a vuoto

La tensione indotta dipende dal flusso magnetico, oltre che dal tipo di avvolgimento, dal numero di conduttori e dalla velocità di rotazione. Il flusso magnetico si regola intervenendo sulla corrente di eccitazione. Per bassi valori dell'induzione magnetica, quibdi del flusso, la riluttanza del ferro è trascurabile rispetto a quella del traferro e la corrente di eccitazione serve esclusivamente per la caduta di tensione magnetica sul traferro. Poiché la riluttanza del traferro è costante, c'è proporzionalità diretta tra tensione indotta e corrente di eccitazione. Quando il ferro entra in zona di saturazione, la caduta di tensione magnetica nel Ferro non è più trascurabile e cresce al crescere del flusso, quindi all'aumentare della corrente di eccitazione. La caratteristica a vuoto $E, I e$ assume allora l'andamento di figura

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Per avere la tensione E0, La correte di eccitazione OA serve per la caduta di tensione magnetica nel traferro; la corrente AB per la caduta di tensione magnetica nel ferro.

con cambiamento di scala in ordinata si ha il flusso ed in ascisse la forza magnetomotrice (caratteristica di magnetizzazione)

Esercizio

a)

Un alternatore bipolare trifase ha dodici cave nello statore. In ogni cava ci sono $n i = 24$ conduttori. L'avvolgimento è a passo intero. Il valore del flusso polare è di $\Phi=0{,}024 \, \text{Wb}$ e la sua distribuzione al traferro è sinusoidale. Il collegamento è a stella. La frequenza è $f= 50 \, \text{Hz}$ .
Calcolare la tensione a vuoto concatenata.

Soluzione

Basta applicare la formula

${U_0} = \sqrt 3 \times 2{k_f}{k_i}{k_r}f\phi N$

dove

$\begin{array}{l} {k_f} = 1{,}11\\ {k_r} = 1\\ \\ q = \frac{Q}{{2p \times 3}} = \frac{{12}}{6} = 2\\ \\ \alpha = \frac{{2\pi }}{{12}} = \frac{\pi }{6}\\ \\ {k_i} = \frac{{\sin \frac{{q\alpha }}{2}}}{{q\sin \frac{\alpha }{2}}} = \frac{{\sin \frac{{2\pi }}{{12}}}}{{2\sin \frac{\pi }{{12}}}} = 0,966\\ \\ N = 2pq{n_i} = 2 \times 2 \times 24 = 96 \end{array}$

Quindi
${E_0} = 2{,}11 \times 0{,}966 \times 50 \times 0{,}024 \times 96 = 247 \, {\rm{V}}$
$U_0=\sqrt{E_0}= 428 \, {\rm{V}}$

b)

Quanto vale la tensione indotta se, oltre alla componente fondamentale dell'induzione che dà luogo al flusso precedente, esistono anche una componente di tera e quinta armonica che danno luogo, rispettivamente, a flussi di valore efficace $\Phi_3=2{,}64 \, \text{mWb}$ e $\Phi_5=1{,}68 \, \text{mWb}$
Soluzione
I coefficienti di raccorciamento risultano pari ad 1 essendo l'avvolgimento a passo intero ( $β = 0$ ). I coefficienti di avvolgimento relativi alle due armoniche valgono

$\begin{array}{l} {k_{i3}} = \frac{{\sin \left( {3\frac{{2\pi }}{{12}}} \right)}}{{2\sin 3\frac{\pi }{{12}}}} = \frac{1}{{\sqrt 2 }} = 0,707\\ \\ {k_{i5}} = \frac{{\sin \left( {5\frac{{2\pi }}{{12}}} \right)}}{{2\sin 5\frac{\pi }{{12}}}} = 0,259 \end{array}$

e le tensioni d'armonica corrispondenti hanno valore efficace di fase
$\begin{array}{l} {E_3} = 2{,}22 \times 0{,}707 \times 2{,}64 \times {10^{ - 3}} \times 150 \times 96 = 59{,}7 \, {\rm{V}}\\ {E_5} = 2{,}22 \times 0{,}259 \times 1{,}68 \times {10^{ - 3}} \times 250 \times 96 = 23{,}2 \, {\rm{V}} \end{array}$

Il valore efficave della tensione di fase è allora
$E = \sqrt {E_0^2 + E_3^2 + E_5^2} = \sqrt {{{247}^2} + {{59{,}7}^2} + {{23{,}2}^2}} = 255 \, {\rm{V}}$
mentre quello della tensione concatenata è
$U = \sqrt {{{\left( {\sqrt 3 {E_0}} \right)}^2} + {{\left( {\sqrt 3 {E_5}} \right)}^2}} = \sqrt {3 \times {{247}^2} + 3 \times {{23{,}2}^2}} = 430{\rm{V}}$
Nelle tensioni concatenate infatti le terze armoniche, ed i loro multipli, presenti nelle tensioni di fase, scompaiono in quanto le terze armoniche sono in fase e le concatenate ne sono la differenza.

c)

Quanto valgono le tensioni precedenti se si adotta un passo raccorciato con $\beta=\frac{\pi}{6}$
Soluzione
Si modificano i coefficienti di accorciamento
$\begin{array}{l} {k_{r1}} = \cos \left( {\frac{\beta }{2}} \right) = \cos \left( {\frac{\pi }{{12}}} \right) = 0{,}966\\ {k_{r3}} = \cos \left( {3\frac{\beta }{2}} \right) = \cos \left( {\frac{\pi }{4}} \right) = 0{,}707\\ {k_{r5}} = \cos \left( {5\frac{\beta }{2}} \right) = \cos \left( {\frac{{5\pi }}{{12}}} \right) = 0{,}259 \end{array}$
quindi le tensioni valgono
$\begin{array}{l} {E_0} = 2{,}22 \times 0{,}966 \times 0{,}966 \times 0{,}024 \times 50 \times 96 = 239{\rm{V}}\\ {E_3} = 2{,}22 \times 0{,}707 \times 0{,}707 \times 2{,}64 \times {10^{ - 3}} \times 150 \times 96 = 42{,}2{\rm{V}}\\ {E_5} = 2{,}22 \times 0{,}259 \times 0{,}259 \times 1{,}68 \times {10^{ - 3}} \times 250 \times 96 = 6{\rm{V}}\\ \\ E = \sqrt {E_0^2 + E_3^2 + E_5^2} = \sqrt {{{239}^2} + {{42{,}2}^2} + {6^2}} = 243{\rm{V}}\\ U = \sqrt {{{\left( {\sqrt 3 {E_0}} \right)}^2} + {{\left( {\sqrt 3 {E_5}} \right)}^2}} = \sqrt {3 \times {{239}^2} + 3 \times {6^2}} = 414{\rm{V}} \end{array}$

I valori efficaci sono ridotti, ma le forme d'onda sono migliorate per il minor contenuto armonico.

Bibliografia

Appunti di macchine elettriche - Ciro Di Pieri - Ed. CLEUP - Ia ed. settembre 1970; ristampa novembre 1991
Macchine elettriche rotanti - M.Andriollo - G. Martinelli - A. Morini - CLEUP , 1998

ElectroYou - la comunità dei professionisti del mondo elettrico

La tensione indotta in una macchina sincrona

Indice

Come funziona un generatore sincrono

Tensione indotta a vuoto in un conduttore di statore

Avvolgimento

Fattore di avvolgimento

Fattore di accorciamento

Armoniche

Avvolgimenti trifasi

Caratteristica a vuoto

Esercizio

a)

b)

c)

Bibliografia

Inserisci un commento

Argomenti correlati

Tag Cloud

Informazioni

Seguici

Pubblicità

Credits