Indice |
La prima legge "non basta"...
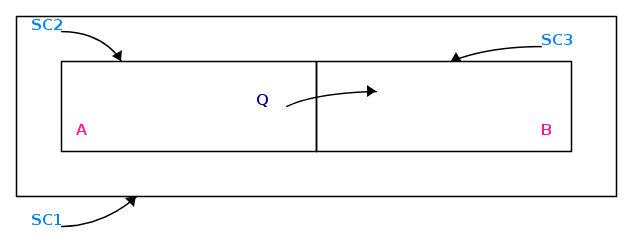
Prendiamo in esame un sistema isolato, SI, fatto in modo tale da essere composto da due sottosistemi, dei quali uno ha una temperatura maggiore dell'altro.
Ad esempio, supponiamo che i due sottosistemi, A e B, siano due pezzi di metallo a contatto tra di loro e che all'istante iniziale si abbia :

Guardiamo ora quanto raffigurato schematicamente nella figura che segue e cerchiamo di spiegarne il significato:
Dall'esperienza di tutti i giorni, si osserva, nell'intervallo di tempo Δθ, il trasferimento di energia, in modalità calore, dal sistema A al sistema B.
Tenendo conto della sola prima legge della termodinamica relativamente alle tre superfici di controllo SC1, SC2 ed SC3, si ha:



In sostanza, l'energia di A diminuisce, quella di B aumenta dello stesso ammontare e quella del sistema isolato SI rimane immutata.
Per assurdo supponiamo che l'interazione avvenga nel senso opposto, cioè da B ad A; sempre secondo la prima legge si avrebbe:



Cioè l'energia di A aumenterebbe, mentre diminuirebbe quella di B in misura uguale e quella di SI rimarrebbe ancora immutata.
Da quanto finora detto si deduce che la prima legge non fornisce informazione alcuna sul verso dell'interazione. Qualunque sia il verso dell'interazione essa afferma comunque il principio della conservazione.
Se facciamo sempre riferimento alla figura schematica di cui sopra, l'energia del sistema complessivo (SC1) rimane immutata : da un punto di vista termodinamico ci chiediamo se sia più conveniente la situazione iniziale o quella vista pocanzi.
Viene da sé pensare che le due situazioni non sono proprio equivalenti : non si osserva mai infatti il passaggio spontaneo (e si sottolinea spontaneo) da un sistema a temperatura inferiore ad uno a temperatura maggiore.
Sarebbe un po' come se una tazza di caffè, alla temperatura di 25° C, posta in un ambiente ad una temperatura di 15° C, si riscaldasse piuttosto che raffreddarsi.
Affinché avvenga questo "trasferimento in senso opposto" è necessario forzare il flusso di energia nel verso delle temperature crescenti : questo ovviamente richiede un costo in termini di energia.
Si deduce quindi che suddividere l'energia tra più sottosistemi a temperatura differente è una "questione" importante seppur l'energia del sistema complessivo rimanga immutata.
Si può quindi parlare anche di qualità dell'energia che dipende dalla temperatura alla quale si trova.
La seconda legge della termodinamica riesce a fornire delle risposte in tal senso.
Per i sistemi chiusi
Introdurremo tra poco una grandezza, l'entropia, la cui equazione di bilancio costituisce quella che è la seconda legge della termodinamica, prima citata.
Postuliamo quindi l'esistenza di una proprietà termodinamica estensiva, chiamata entropia. Deriva dalla parola greca εντρωπη che può essere tradotta con evoluzione.
E' una grandezza non conservativa e che è quindi caratterizzata da generazione; il suo flusso attraverso la superficie di controllo del generico sistema termodinamico è legato a quello di energia solo nella forma calore, secondo la relazione che segue :

dove:
- Φ(S) è il flusso di entropia;
- Q è la quantità di energia trasferita nella modalità calore attraverso un elemento della superficie di controllo del sistema termodinamico;
- T è la temperatura assoluta dell'elemento della superficie di controllo (se invece la superficie di controllo racchiude un unico sistema termodinamico a temperatura uniforme, T è la temperatura dell'intero sistema).
Come abbiamo detto prima, l'entropia si genera e questa sua caratteristica è esprimibile mediante la disuguaglianza :

Scriviamo quindi l'equazione di bilancio della proprietà (estensiva lo ricordiamo) entropia.
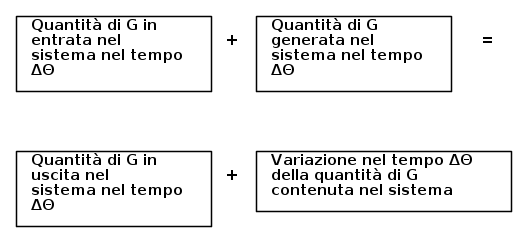
Prima di scrivere l'equazione di bilancio, facciamo una piccolissima digressione su cosa sia, formalmente parlando, una equazione di bilancio.
Dato un sistema termodinamico, per ciascuna proprietà estensiva, chiamiamola ad esempio G, è possibile formulare una equazione di bilancio secondo uno "schema a blocchi", come segue :
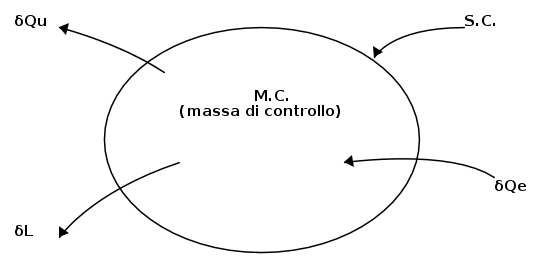
Precisato quanto sopra, consideriamo ai fini della scrittura dell'equazione di bilancio, la seguente figura schematica, in cui abbiamo un sistema chiuso che interagisce energeticamente, secondo le due modalità (calore e lavoro) con l'ambiente esterno :
L'equazione di bilancio sarà :

A tal proposito osserviamo che :
- il flusso entropico, come detto anche prima, non è legato all'interazione energetica in modalità lavoro;
- dato che la temperatura del sistema è generalmente variabile nel tempo, si è preso in considerazione un intervallo di tempo infinitesimo in modo tale che la (1), cioè l'espressione del flusso entropico, sia data dal rapporto tra le quantità elementari di energia termica e la temperatura del sistema supposta uniforme;
- i differenziali non esatti sono stati indicati con il simbolo "δ".
Se indichiamo con δQ l'energia termica netta entrante possiamo scrivere in forma più compatta :

che risulta essere la seconda legge della termodinamica nella forma differenziale (per una massa di controllo).
Da essa deduciamo che la variazione di entropia del sistema è pari alla somma del flusso di entropia attraverso la superficie di controllo e dell'entropia che si è generata al suo interno.
Volendo riferirsi alle grandezze specifiche, si può scrivere :

Se ci riferiamo ad un intervallo di tempo finito, per integrazione, otteniamo :


La seconda legge della termodinamica per un sistema isolato si riduce in sostanza a :

In un sistema isolato, quindi, l'entropia, in relazione alle trasformazioni reali che avvengono in esso, è sempre in aumento.
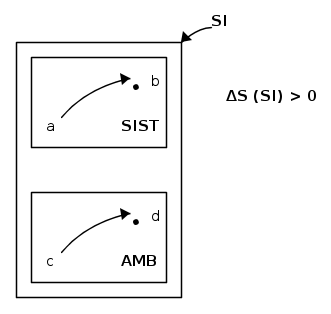
Consideriamo ora un sistema isolato SI che sia composto da un generico sistema termodinamico SIST e dal suo ambiente AMB:
Siano ab e cd le trasformazioni a cui sono rispettivamente soggetti sistema ed ambiente. la seconda legge afferma che l'entropia del sistema isolato sarà aumentata.
Ora ci chiediamo se sia possibile riportare sistema ed ambiente nei loro stati iniziali (a e c rispettivamente).
E' chiaramente evidente che ciò è impossibile. Infatti se si ritornasse negli stati iniziali, il sistema isolato tornerebbe nel suo stato iniziale e anche l'entropia tornerebbe al suo valore iniziale; l'entropia del sistema isolato era però aumentata e tornare al valore iniziale significherebbe che l'entropia deve diminuire, il che è in conflitto con quanto affermato dalla seconda legge della termodinamica.
Quanto detto pocanzi può essere riassunto dicendo che quindi le trasformazioni reali non sono reversibili, cioè che il passaggio del sistema/ambiente da uno stato all'altro è contrassegnato da una traccia indelebile che è la generazione entropica.
Proprio la generazione entropica impedisce di ritornare dallo stato finale a quello iniziale.
Si parla invece di trasformazione reversibile quando si ha a che fare con una trasformazione ideale caratterizzata da generazione entropica nulla.
Quindi, ricapitolando: le trasformazioni reali sono irreversibili; è possibile comunque definire in via concettuale una trasformazione ideale detta "reversibile" per la quale il cammino diretto ha generazione entropica nulla e per la quale è possibile il cammino inverso, anch'esso con generazione entropica nulla, in modo tale che sia il sistema che l'ambiente ritornano al loro stato iniziale senza che rimanga traccia della trasformazione compiuta.
Possiamo così riscrivere la (2) nel modo che segue :

in cui il segno di uguaglianza definisce simbolicamente la trasformazione reversibile.
I fenomeni naturali che causano maggiore o minore irreversibilità si possono dividere in due gruppi :
- il primo gruppo comprende la conversione di energia nella forma lavoro in energia interna (se ne riportano alcuni a titolo di esempio) : fenomeni di attrito, fenomeni di resistenza ohmica, fenomeni di isteresi,
- il secondo gruppo comprende i fenomeni all'interno dei quali si segnala una tendenza spontanea a passare da uno stato di non equilibrio ad uno finale di equilibrio (se ne riportano alcuni a titolo di esempio) : le reazioni chimiche, il mescolamento, l'espansione libera, l'equalizzazione delle temperature.
Quando ci si vuole concentrare su quanto accade al solo sistema, si definisce una trasformazione ideale detta stavolta internamente reversibile tale che sia nulla la generazione di entropia corrispondente.
Consideriamo un tratto elementare della trasformazione, per la seconda legge si avrà :


Sommandole si ha :

Se si tratta di una trasformazione elementare internamente reversibile si ha :

e cioè :

cioè i flussi di entropia che sono relativi alla trasformazione di andata e ritorno sono uguali ed opposti.
La seconda legge della termodinamica per una trasformazione ideale internamente reversibile si può scrivere :



Queste tre relazioni sono note anche come uguaglianza di Clausius.
Confrontando la (0) e la prima delle tre relazioni scritte prima, tenendo conto del fatto che la generazione entropica è sempre positiva, si può scrivere la seguente espressione :

nota come disuguaglianza di Clausius (il segno di uguaglianza è riferito alle trasformazioni internamente reversibili).
Va precisato infine che la generazione di entropia non è una proprietà termodinamica e non va mai confusa con la variazione della proprietà entropia, anche se in alcuni casi possono coincidere (trasformazioni adiabatiche o sistemi isolati).
L'entropia si misura in J / K (J / KgK se specifica) nel S.I. .
Per i sistemi aperti
Considereremo nella trattazione per i sistemi aperti i termini di flusso che sono legati all'ingresso e/o all'uscita di materia attraverso la superficie di controllo che delimita il sistema; tali flussi sono detti convettivi.
Si ipotizza che i flussi attraverso i varchi siano monodimensionali.
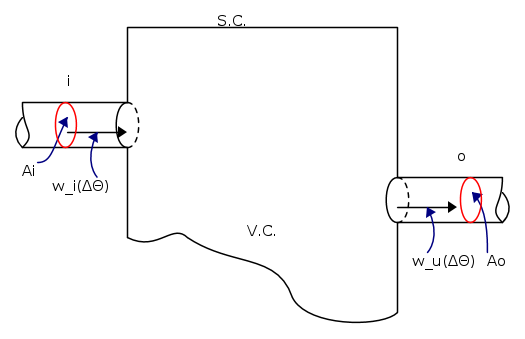
Consideriamo la seguente figura schematica :
Come effetto della velocità del fluido, nell'intervallo di tempo Δθ, i volumetti di base Ai e Ao, rispettivamente entreranno ed usciranno dal volume di controllo V.C. e sono espressi come :

Associate agli elementi di volume ΔVi e ΔVo entreranno ed usciranno le grandezze estensive ad essi relative.
Tenuta presente la figura sopra e le relazioni scritte pocanzi, possiamo ricavare le equazioni che forniscono la quantità di entropia che nell'intervallo di tempo Δθ entra ed esce attraverso il varco di ingresso generico i e il generico varco di uscita o.
Questi contributi si ottengono moltiplicando le masse associate ai volumi entranti ed uscenti per il valore dell'entropia legato alle sezioni corrispondenti :

che possono essere scritte come :

dove  è la portata massica.
è la portata massica.
La (3) fornisce l'espressione del flusso entropico convettivo che va inserita nell'equazione di bilancio.
Le interazioni tra il sistema aperto e l'ambiente che devono essere tenute in considerazione per la scrittura del bilancio di entropia sono :
- flusso entropico associato al flusso energetico nella sola modalità calore, Q / T;
- flusso entropico convettivo associato al flusso di massa,
 .
.
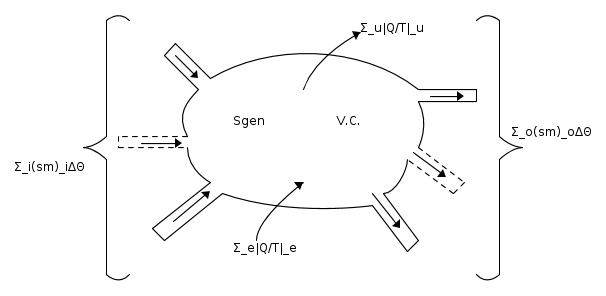
Se consideriamo la seguente figura :
l'equazione di bilancio dell'entropia sarà :

Ponendo :

dividendo ogni termine per Δθ, operando il limite per Δθ tendente a zero e riordinando si ha :

La (4) è la seconda legge della termodinamica per i sistemi aperti e può essere interpretata come segue : la rapidità con cui varia nel tempo l'entropia contenuta nel volume di controllo dipende sia dai flussi entropici che, nelle due forme, attraversano la superficie di controllo, sia dall'entropia generata, a causa delle irreversibilità, nel volume di controllo.
Va ricordato che l'entropia generata si annulla solo per le condizioni ideali di reversibilità.
Se il sistema fosse in condizioni di regime stazionario, il contenuto di entropia relativo al volume di controllo non varia nel tempo :

e l'equazione di bilancio dell'entropia è :

Per approfondire
Per chi volesse approfondire l'argomento, (ringrazio RobertFirpo per la gentile segnalazione) i libri :
- The Laws of Thermodynamics: A Very Short Introduction di Peter Atkins, edito da Oxford University Press :
- la traduzione edita da Zanichelli, intitolata Le regole del gioco. Come la termodinamica fa funzionare l'universo, di Peter Atkins :
Bibliografia
Elementi di termodinamica applicata - Cesarano, Mazzei.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)