ElectroYou - la comunità dei professionisti del mondo elettrico

Indice

1 Premessa all'articolo
2 Le ipotesi di partenza
3 Il significato della temperatura
- 3.1 Qualche riflessione
4 Bibliografia

Premessa all'articolo

Dopo i quattro articoli dedicati ai gas in cui abbiamo parlato di pressione, temperatura, legge dei gas ideali e miscele di gas e dei gas reali, chiudiamo "il capitolo gas" illustrando in via panoramica la teoria cinetica dei gas.
Ci proponiamo in questo articolo di ricavare una relazione tra le velocità molecolari e la temperatura.

Le ipotesi di partenza

La teoria cinetica dei gas fornisce una spiegazione microscopica della legge di Boyle e una descrizione meccanica microscopica della temperatura come misura dell'energia cinetica media delle molecole di un gas.
Le ipotesi di partenza della teoria cinetica dei gas sono le seguenti:

un gas puro consiste in un grande numero di molecole identiche separate da distanze che sono grandi rispetto alle loro dimensioni;
le molecole del gas sono costantemente in moto, in direzioni casuali e con una distribuzione di velocità;
tra una collisione e l'altra le molecole non esercitano forze tra di esse, e quindi tra una collisione e l'altra le molecole si muovono in linea retta con velocità costante;
le collisioni delle molecole con le pareti del recipiente sono elastiche : durante la collisione non c'è perdita di energia.

Il significato della temperatura

Cerchiamo di adoperare la teoria cinetica dei gas per ricavare una relazione tra pressione, volume e moto delle molecole in un gas ideale. Un confronto con la legge dei gas ideali consentirà di comprendere meglio il significato della temperatura.

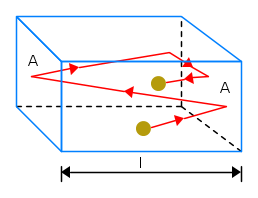
A tal fine consideriamo un recipiente con forma di una scatola rettangolare di lunghezza $l$ con le facce ai due estremi di area $A$ .

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Poniamo nella scatola una singola molecola con velocità $u$ in una certa direzione. Per indicare il valore della velocità in $m / s$ e la direzione del movimento nella figura che segue, la rappresenteremo con una freccia (un vettore) $\overrightarrow{v}$ , la cui lunghezza è uguale al valore della velocità (scalare) $u$ e che punta nella direzione del moto della molecola.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

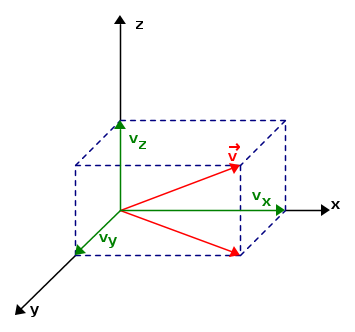
La velocità può essere rappresentata anche dalle sue componenti lungo i tre assi delle coordinate : $v x$ , $v y$ , $v z$ .
Queste sono legate a $u$ dalla relazione del teorema di Pitagora:

$u^{2}=\ v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\ .$

La quantità di moto di una molecola, $\overrightarrow{p}$ , è data dal prodotto tra la sua velocità e la sua massa, $m$ . Quando la molecola compie una collisione elastica con una delle pareti di area $A$ agli estremi della scatola, le componenti lungo $y$ e $z$ della velocità, $v y$ e $v z$ , non cambiano, mentre la componente lungo $x$ (perpendicolare ad $A$ ) cambia di segno, come si può dedurre dalla figura seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

La variazione della quantità di moto lungo la componente $x$ , $Δ p x, m o l$ , è:

$\Delta p_{x,mol}=\ quantit\grave{a}\ di\ moto\ finale\ -\ quantit\grave{a}\ di\ moto\ iniziale\ =$

$m(-v_{x})-mv_{x}=-2mv_{x}\ .$

La quantità di moto totale del sistema (cioè molecola più scatola) deve conservarsi e quindi questa variazione di quantità di moto deve essere eguagliata da una uguale variazione di quantità di moto della parete:

$\Delta p_{x,parete}=2mv_{x}\ .$

Dopo questa collisione con la parete, la molecola inverte la sua direzione e finisce per collidere con la parete opposta e ritorna dopo ancora verso la prima parete. Fra i due urti può capitare anche che collida con la parete superiore od inferiore oppure con quelle laterali.
Questi urti, però, non cambiano $v x$ e il tempo trascorso tra due collisioni con la parete iniziale non cambia (si veda in proposito la prima figura dell'articolo).
La distanza percorsa nella direzione $x$ è $2 l$ e la componente della velocità in quella direzione è $v x$ , per cui il tempo che intercorre tra le collisioni tra le due pareti opposte è:

$\Delta t=\ \frac{2l}{v_{x}}\ .$

Ogni secondo la quantità di moto trasferita alla parete sarà data dalla variazione della quantità di moto per collisione, $Δ p x, p a r e t e$ diviso per $Δ t$ :

$\frac{\Delta p_{x,parete}}{\Delta t}=\ \frac{2mv_{x}}{2l/v_{x}}=\ \frac{mv_{x}^{2}}{l}\ .$

Per la seconda legge di Newton la forza esercitata sulla parete dalle ripetute collisioni della molecola è:

$f=\ ma=\ m\frac{\Delta v}{\Delta t}=\ \frac{\Delta p}{\Delta t}=\ \frac{mv_{x}^{2}}{l}$

Supponiamo ora che nella scatola a muoversi sia un numero $N$ grande di molecole indipendenti di massa $m$ con componenti di velocità nella direzione $x$ uguale a $v x 1$ , $v x 2$ , $v x 3$ e così via.

La forza totale esercitata sulla parete dalle $N$ molecole è pari alla somma delle forze esercitate da ciascuna delle molecole:

$F=\ \frac{mv_{x1}^{2}}{l}+\frac{mv_{x2}^{2}}{l}+\ \cdots\ +\frac{mv_{xN}^{2}}{l}=\ \frac{Nm}{l}\overline{v_{x}^{2}}$

dove:

$\overline{v_{x}^{2}}=\ \frac{1}{N}(v_{x1}^{2}+v_{x2}^{2}+\ \cdots\ +v_{xN}^{2})\ .$

La quantità $\overline{v_{x}^{2}}$ è la media dei quadrati delle componenti lungo $x$ della velocità delle $N$ molecole e si ottiene sommando $\overline{v_{x}^{2}}$ per le $N$ molecole e dividendo per $N$ . La pressione è la forza totale esercitata sulla parete divisa per l'area $A$ :

$P=\ \frac{F}{A}=\ \frac{Nm}{Al}\overline{v_{x}^{2}}\ .$

Dato che $A l$ è il volume $V$ della scatola, si conclude che:

$PV=\ Nm\overline{v_{x}^{2}}\ .$

Le molecole gassose non hanno una direzione preferenziale di movimento, per cui $\overline{v_{x}^{2}}$ , $\overline{v_{y}^{2}}$ e $\overline{v_{z}^{2}}$ saranno uguali tra di loro. Si ha quindi che:

$u=\ \overline{v_{x}^{2}}+\overline{v_{y}^{2}}+\overline{v_{z}^{2}}= 3\overline{v_{x}^{2}}$

e cioè:

$PV=\ \frac{1}{3}Nm\overline{u^{2}}$

dove $\overline{u^{2}}$ è la velocità quadratica media delle molecole del gas.

Dalla legge dei gas ideali:

$PV=\ nRT$

si può scrivere:

$\frac{1}{3}Nm\overline{u^{2}}=\ nRT\ .$

Abbiamo ottenuto con questa equazione una relazione tra le velocità molecolari e la temperatura, che può essere anche semplificata.
Nell'equazione compare il numero di molecole $N$ a sinistra e il numero di moli $n$ a destra.

Ricordando che:

$N=\ nN_{A}$

dove $N A$ è il numero di Avogadro, dividendo ambo i membri per $n$ otteniamo:

$\frac{1}{3}N_{A}m\overline{u^{2}}=\ RT\ (1)\ .$

Qualche riflessione

Sull'equazione $(1)$ possiamo fare due osservazioni.

PRIMA OSSERVAZIONE
L'energia cinetica di una molecola di massa $m$ che si muove con velocità $u$ è data da:

$\ \frac{1}{2}mu^{2}\ ,$

quindi l'energia cinetica media di $N A$ molecole (1 mole) è pari a :

$\overline{E}=\ \frac{1}{2}N_{A}mu^{2}\ .$

Questo è il lato sinistro dell'equazione, ma con il fattore $\frac{1}{2}$ invece che $\frac{1}{3}$ :

$\overline{E}=\ N_{A}m\overline{u^{2}}=\ \frac{3}{2}\times \left ( \frac{1}{3}N_{A}m\overline{u^{2}} \right )=\ \frac{3}{2}RT\ .$

L'energia cinetica di una singola molecola, $\overline{\varepsilon }$ , si ottiene dividendo $\overline{E }$ per il numero di Avogadro:

$\overline{\varepsilon }=\ \frac{3}{2}k_{B}T$

dove $k B$ è detta costante di Boltzmann, pari a $R / N A$ . L'energia cinetica media delle molecole di un gas dipende solo dalla temperatura e non dipende dalla massa delle molecole o dalla loro densità numerica.
Questa relazione è il risultato più importante della teoria cinetica dei gas.

SECONDA OSSERVAZIONE
Notiamo che se $m$ è la massa di una singola molecola allora la massa di 1 mole di molecole è pari a $N A m$ , che verrà indicato con il simbolo $M$ .
Possiamo scrivere quindi che:

$\overline{u^{2}}=\ \frac{3RT}{M}\ .$

La velocità quadratica media di una molecola di gas sarà direttamente proporzionale alla temperatura e inversamente proporzionale alla sua massa.
Le molecole si muovono più velocemente a temperatura più elevate, mentre molecole leggere si muovono più velocemente di quelle pesanti alla stessa temperatura.

Bibliografia

Chimica moderna - Oxtoby, Gillis, Campion.

ElectroYou - la comunità dei professionisti del mondo elettrico

La teoria cinetica dei gas: velocità molecolari e temperatura

Indice

Premessa all'articolo

Le ipotesi di partenza

Il significato della temperatura

Qualche riflessione

Bibliografia

Inserisci un commento

Argomenti correlati

Tag Cloud

Informazioni

Seguici

Pubblicità

Credits