ElectroYou - la comunità dei professionisti del mondo elettrico

Indice

1 Premessa
2 Il problema
3 Soluzione matematica
4 Soluzione con Laplace
5 Soluzione grafica
6 Soluzione con le differenze finite
7 Simulazione
8 Conclusioni

Premessa

L'analisi dei transitori nei circuiti elettrici è uno degli argomenti più frequenti nel Forum di EY.
Si tratta in genere di stabilire l'andamento nel tempo di tensioni o correnti alla brusca modifica del circuito dovuta alla chiusura (o all'apertura) di un interruttore. Il "transitorio" è appunto quel periodo di tempo che intercorre fra un regime stazionario prima e dopo l'intervento dell'interruttore.
L'analisi comporta la soluzione di equazioni differenziali di una certa complessità ma che può essere facilitata dall'uso del computer. Esamineremo quindi un circuito particolarmente semplice, ma con metodi di soluzione diversi, resi possibili appunto dall'uso del PC.
Personalmente ritengo infatti che il computer sia sorta di "protesi" del cervello che permette di ragionare meglio (così come gli occhiali permettono di leggere meglio). E' però evidente che se uno non sa leggere, gli occhiali non migliorano la situazione, così come non serve avere un computer se non lo si sa sfruttare.

Il problema

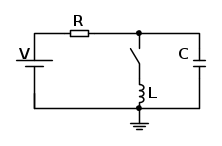
Il semplice problema proposto è il seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Dato quindi un RC alimentato da una tensione costante V, è chiaro che vi sarà un primo transitorio in cui C si carica alla tensione V con un andamento esponenziale $V(1-e^{-\frac{t}{R\cdot C}})$ .
Dopo un tempo >5RC, si può ritenere concluso questo transitorio, ovvero che si sia raggiunto praticamente la condizione di regime.
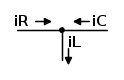
A questo punto può essere chiuso l'interruttore che inserisce nel circuito l'induttore L e l'equilibrio delle correnti istantanee nel nodo

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

diventa: $i L = i R + i C$
Tale nodo avrà una tensione istantanea v(t) (che d'ora in poi chiameremo semplicemente v), con cui possiamo esprimere le correnti:
$i_L=\frac{1}{L}\cdot\int_{0}^{t} v\,\rm{d}t\quad\quad\quad i_R= \frac{V-v}{R}\quad \quad\quad\quad i_C=-C\cdot v\,\rm{d}t$
Derivando ciascun membro e sostituendoli nell'equazione del nodo, si ottiene:
$v''+\frac{1}{R\cdot C}\cdot v'+\frac{1}{L\cdot C}\cdot v =0$
La derivazione comporta però la perdita della costante V e la soluzione dovrà essere cercata in una famiglia di curve fissando i valori iniziali $: \quad v(0)=V \quad e \quad v'(0)=0$ .

Soluzione matematica

Abbiamo visto che la tensione del nodo è espressa da un'equazione differenziale del secondo ordine, omogenea e a coefficienti costanti (vedi link, par.2, di cui conserveremo la simbologia), del tipo
$y'' + p y' + q y = 0$
La soluzione prevede la ricerca delle radici dell'equazione $:\quad r^2+pr+q=0$ ,
che saranno i coefficienti della funzione cercata.
Normalmente $p=\frac{1}{R\cdot C}$ e $q=\frac{1}{L\cdot C}$ sono valori numerici (R,L,C dati), ma manterremo qui la notazione sombolica per generalizzare l'analisi.

Dal link citato ricaviamo che se $p 2 > 4 q$ la soluzione sarà un'oscillazione , altrimenti un'esponenziale .
Nel nostro caso, con le sostituzioni precedenti, il comportamento oscillatorio si avrà per $R>\frac{1}{2} \cdot \sqrt{\frac{L}{C}}$ . In tal caso la soluzioni di r saranno complesse coniugate ( $\alpha \pm i \beta$ )
La soluzione generale (vedi link) è:
$y=e^{\alpha \cdot t} \cdot (C1 \cdot \cos(\beta \cdot t)+C2 \cdot \sin(\beta \cdot t))$
ma considerando le condizioni iniziali $y (0) = V$ e $y'(0) = 0$ , risulta C1=V e C2=0,e la soluzione finale sarà quindi;
$v=V \cdot e^{\alpha \cdot t} \cdot \cos(\beta \cdot t)$
Non rimane ora che calcolare $α$ e $β$ dall'equazione
$r^2+\frac{r}{R \cdot C}+ \frac{1}{L \cdot C}=0$
da cui risulta $:\quad \alpha =-\frac{1}{2 \cdot R \cdot C}\quad ,$ e $:\quad i\beta=\frac{1}{2} \cdot \sqrt{ \left (\frac{1}{R \cdot C}\right )^2-\frac{4}{L \cdot C}}$

Come si vede, anche per un caso semplice, il procedimento matematico non è affatto semplice.

Soluzione con Laplace

Un approccio più semplice è l'utilizzo del metodo di Laplace.
L'equilibrio delle correnti nel nodo visto in precedenza, porta ad un'equazione in s equivalente all'equazione diffrenziale del precedente paragrafo.
Le singole correnti possono infatti essere espresse in funzione della tensione v del nodo,
in questo modo: $:\quad i_L=\frac{v}{L\cdot s} \quad \quad i_R=\frac{V-v}{R} \quad \quad i_C=-C\cdot v \cdot s$ ,

quindi l'equazione diventa $: \quad \frac{v}{L\cdot s}=\frac{V-v}{R}- C\cdot v \cdot s$

che può essere riscritta così $:\quad v\cdot s^2+\frac{v}{R \cdot C}\cdot s+\frac{v}{L \cdot C}\, = \, 0$

(si osserva che la tensione V è costante, quindi Vs è nulla)
Per ricavare l'espressione di v(s) funzione delle sue derivate e dei valori iniziali, denominiamo y2 la derivata seconda di v, y1 la derivata prima e y0 la funzione v(s) cercata.
Useremo per questo il computer con programma di matematica simbolica (qui viene utilizzato Mathcad) dando direttamente i valori delle variabili in gioco per ottenere già un'espressione numerica in s.

Come si vede, il sistema per trovare le espressioni in s delle 3 variabili y0,y1,y2 tiene conto delle relazioni fra queste (y0 è l'integrale di y1 più la condizione iniziale di V a gradino, e così via).
Il risultato che più ci interessa è ovviamente l'espressione di y0, cioè v(s) che antitrasformata (sempre automaticamente da Mathcad), ci dà l'espressione di v(t) cercata.
Nel caso in esame, con i valori indicati risulta la cosinusoide smorzata (tendente a zero) con coefficiente di smorzamento $\alpha=\frac{1}{2}$ e pulsazione $β = 14.13$ , esattamente corrispondenti a quanto ricavabile dalla soluzione matematica vista precedentemente.

Soluzione grafica

Spesso è più utile avere come risultato direttamente un grafico, anziché passare attraverso la funzione matematica. In questo caso si può ricorrere ad un metodo approssimato (Runge-Kutta) che permette il tracciamento del transitorio data l'equazione differenziale corrispondente.

La procedura in Mathcad è semplicissima: si definisce un vettore y dei valori iniziali (nel caso in esame v(0)=V e v'(0)=0), un secondo vettore D delle derivate prima e seconda, ed infine una matrice Z con la definizione della variabile (y) dell'intervallo di tempo (0-5s), del numero di campionamenti (100) ed infine il vettore delle derivate.
La matrice Z ha come prima colonna ( $Z < 0 >$ ) il tempo e nella seconda ( $Z < 1 >$ ) l'andamento della soluzione.
Si può facilmente verificare che corrisponde alle soluzioni precedenti.

Soluzione con le differenze finite

Una altro metodo, più diretto, per ottenere la soluzione grafica è il ricorso alle differenze finite.
Invece di derivate ed integrali, per esprimere iC ed IL si usano espressioni approssimate (le differenze finite appunto) che ne rappresentano la variazione nel tempo $Δ T$ prefissato (più è piccolo $Δ T$ e più preciso è il risultato).

$i_{C_{n}}= -C \cdot \frac{v_{n}-v_{n-1}}{\Delta T}\quad ($ da cui si può ricavare $v n)$

$i_{L_{n}}=i_{L_{n-1}}+\frac{v_{n-1}}{L}\cdot \Delta T$

Le equazioni devono essere poi raccolte in un vettore per assicurare il calcolo simultaneo ad ogni n. Per esigenze di calcolo si è dovuto poi sostituire $i C n - 1$ ad $i C n$ con un errore del tutto trascurabile.

La rapprecentazione grafica è così immediata:

Si noti che il metodo ha il vantaggio di poter rappresentare nello stesso modo anche l'andamento di ciascuna corrente. E' superfluo poi ricordare che, una volta impostato il programma, qualsiasi variazione nei dati di partenza porta all'aggiornamento automatico del grafico, quindi si possono studiare comodamente le influenze di ciascun parametro sul risultato. Particolarmente interessante è il caso con R=35 Ohm (resistenza critica, che segna il passaggio da oscillatorio ad aperiodico).

Simulazione

La simulazione è la forma più semplice di soluzione. Anzi è troppo semplice, tanto da farla ritenere diseducativa (e quindi osteggiata) da molti insegnanti.
Con un programma di simulazione basta disegnare il circuito per ricavarne tutti i dati che si vogliono, compreso l'andamento di una certa grandezza nei transitori (Transient Analysis).

Ecco il caso qui trattato, simulato con Microcap

Qui il ciclo è completo, con il transitorio iniziale di carica del condensatore all'atto dell'alimentazione ed un relè che dopo 5s chiude il contatto che inserisce l'induttore.
Scegliendo di tracciare la tensione al nodo, si ricava immediatamente l'andamento relativo.

Conclusioni

Si è visto un caso particolarmente semplice di circuito,(ma spesso anche casi più complessi possono essere ricondotti a questa forma utilizzando Thevenin), con approcci diversi per arrivare alla soluzione finale. Lascio al lettore trarre le conclusioni da tale confronto.

ElectroYou - la comunità dei professionisti del mondo elettrico

Analisi dei transitori con il PC

Indice

Premessa

Il problema

Soluzione matematica

Soluzione con Laplace

Soluzione grafica

Soluzione con le differenze finite

Simulazione

Conclusioni

Inserisci un commento

Argomenti correlati

Tag Cloud

Informazioni

Seguici

Pubblicità

Credits