Il microprocessore ha quarant'anni e il suo impiego nelle elaborazioni di dati necessarie all'automazione industriale è fuori discussione, ma come si facevano queste elaborazioni prima che ci fosse il microprocessore?
E' vero che allora l'automazione industriale era ai primi passi, tuttavia le esigenze di calcolo erano tali che si cercava comunque di risolvere in qualche modo i problemi, utilizzando la tecnologia del tempo. Essendo allora imperante l'elettronica analogica, è ovvio che gran parte di questi problemi venivano risolti con calcolo analogico, tuttavia i progressi delle tecniche digitali già all'inizio degli anni '60 permettevano calcoli numerici mediante l'uso di contatori d'impulsi (vedi [1][2][4][5][7][8]). Si può infatti dire che lo sviluppo delle tecnologie digitali (almeno nel campo delle applicazioni industriali) è iniziato con la realizzazione di contatori a transistor a conteggio in sistema binario oppure anche in decimale (BCD, decimale codificato in binario).

L'estrema rapidità di conteggio permetteva infatti misurare con grande precisione ad es. la velocità periferica di un rullo (e quindi del prodotto trasportato), con indicazione numerica di questa velocità.
Altre importanti applicazioni erano i posizionamenti programmati di organi meccanici (vedi [3][6]), che rendevano possibile funzionamenti automatici altamente flessibili (senza condizionamenti fissi).
Erano soluzioni allora estremamente costose (una "decade" di conteggio richiedeva un'intera scheda!), giustificate solo dall'importanza dell'impianto a cui venivano applicate, ma la cosa interessante che questo articolo vuole evidenziare, è la possibilità di svolgere anche veri e propri calcoli numerici

Somme e sottrazioni

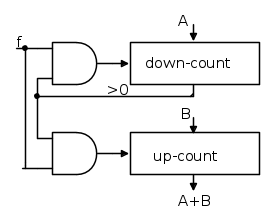
Un contatore elettronico, nella sua forma completa, ha la possibilità di essere "precaricato" con un certo valore ed ha la possibilità scelta fra conteggio progressivo (up-counter) degli impulsi di ingresso, oppure regressivo (down-counter).
E' quindi elementare immaginare che con due contatori sia possibile effettuare una somma fra 2 numeri.
Dati infatti 2 numeri interi, A e B, basta caricare A nel primo contatore (predisposto in down) e B nel secondo (predisposto in up), e poi inviare una frequenza d'impulsi (f) agli ingressi di entrambi finché il primo non risulti azzerato. E' ovvio che quando il primo contatore raggiunge lo zero, il secondo conterrà un numero uguale ad A+B.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

E' ovvia la variante per la sottrazione: supponendo di voler ottenere B-A (con A<B), basta predisporre anche il secondo contatore per conteggio down. In questo caso quando il primo contatore è azzerato, il conteggio viene bloccato lasciando nel secondo il valore B-A.

Moltiplicazioni

Un po' più complesse sono le configurazioni per la moltiplicazione e la divisione (ovviamente sempre fra numeri interi).
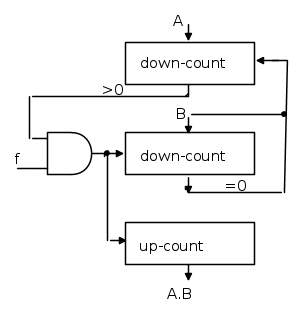
Vediamo la moltiplicazione. Il principio è semplice, ma richiede 3 contatori: per moltiplicare A per B posso caricare i due numeri nei primi 2 contatori predisposti in down, poi inviare impulsi al secondo e al terzo (in up) in modo che quando il secondo è azzerato, nel terzo risultano accumulati B impulsi.
A questo punto basta togliere un impulso dal primo contatore, cioè da A, ripristinando il valore di B nel secondo e continuare così finché il primo contatore è azzerato.
In altre parole si caricano nel terzo contatore B impulsi per ogni decremento di A, quindi quando il primo contatore è a zero, nel terzo risulteranno A.B impulsi.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Divisioni

Un principio analogo può essere eseguito per le divisioni: dato A>B, si sottrae da A un numero di impulsi equivalente a B tante volte finché A non è azzerato.Contando nel terzo contatore il numero di volte in cui il contatore di B si è azzerato, si ottiene la parte intera di A/B
Trattando numeri interi, può essere comodo dividere la frequenza degli impulsi entranti nel primo contatore in modo da poter calcolare anche i possibili decimali della divisione.
Ed ecco una possibile configurazione:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

In questo caso, con una divisione per 100 degli impulsi contati nel primo contatore, siottiene il risultato moltiplicato per 100 (equivalente a 2 decimali).

Una configurazione del genere permette ad es. l'indicazione numerica della velocità di un oggetto che si muove fra due traguardi fissi, misurando digitalmente il tempo: .

Attualmente, anche se una decade è ridotta ad un integrato e a costi irrisori, non c'è convenienza ad assemblare una manciata di integrati rispetto alla semplicità di un micro. Tuttavia è rimasta valida una soluzione già utilizzata negli anni '60, nota come rate multiplier e che oggi richiede un solo integrato.

Il "rate multiplier"

Nelle misure numeriche di velocità, già accennate all'inizio, doveva spesso essere considerato il diametro del cilindro a cui era accoppiato il generatore d'impulsi. Se questo diametro era fisso, non vi erano problemi ad inserirlo nella formula che stabiliva il tempo di conteggio, ma se poteva essere variabile (per usura o per rettifica) bisognava prevedere la possibilità di tarare facilmente lo strumento, almeno entro un qualche percento.
La tecnica che veniva usata era semplicemente basata sull'eliminazione di impulsi ("pulse skip") in modo da adattare la frequenza al rapporto voluto. In pratica venivano differenziati i fronti d'onda delle uscite BCD della decade e venivano utilizzati, mediante selettori o matrici a diodi, per "saltare" un cero numero di impulsi su quella decade.
Una simulazione in MicroCap9, mostra il risultato che si può ottenere con un circuito del genere:

La frequenza in ingresso (fin) è qui divisa per 2 prima di essere immessa nel circuito di skip. Questo limita la possibile riduzione a ca. il 50%: su 20impulsi ne possono essere "saltati", a scelta, da 0 a 9.
In corrispondenza dei fronti positivi delle uscite binarie della decade, può essere infatti abilitato il circuito che elimina l'impulso che segue.
Nella figura sono infatti abilitati sia l'uscita dal primo stadio (divisione per 5) che quella del secondo (divisione per 2), quindi in totale 7 impulsi su 20.
In definitiva ogni 20 impulsi entranti, ne usciranno 13 (fout, come si può vedere dalla simulazione), cioè la frequenza entrante sarà moltiplicata per il rapporto 13/20 (da cui il nome di rate multiplier).

Gli sviluppo dei circuiti integrati hanno reso obsoleta la differenziazione dei fronti d'onda mediante condensatori ed è tuttora utilizzabile l'integrato CMOS 4089.
Come si può vedere dal suo datasheet, si tratta di un contatore a 4 bit, in binario puro, quindi con conteggio fino a 16 (0-15), con la possibilità di predisporre quanti impulsi (su 16) si vogliono in uscita. Essendo intrinsecamente un generatore di rapporto di frequenze, può servire a semplificare le configurazioni di calcolo viste in precedenza.
Vale comunque l'osservazione fatta in precedenza sulla "convenienza" odierna di soluzioni di questo tipo invece di micro: solo in casi speciali e particolarmente semplici risulterebbero giustificati.

Riferimenti

Per chi avesse un interesse storico ad un approfondimento delle tecnologie degli anni '60 in questo campo, segnalo alcuni miei articoli dell'epoca:
[1] Circuiti contatori d'impulsi per misure e regolazioni numeriche - Rendiconti AEI - 1962
[2] Strumenti numerici per misure di precisione nei comandi sezionali - Rivista MARELLI -8-1963
[3] Circuiti sommatori con elementi NOR per controlli industriali - Rendiconti AEI - 1963
[4] Strumenti numerici PRODAC - Rivista MARELLI -6-1964
[5] Strumentazione numerica in un laminatoio continuo a caldo - Rivista MARELLI -6-1966
[6] Evoluzione nei sistemi di posizionamento numerico PRODAC - Rivista MARELLI -9-1967
[7] Strumenti numerici per applicazioni industriali - Rivista MARELLI -11-1968
[8] Nuovi sviluppi nelle regolazioni numeriche di velocità - Rendiconti AEI - 1969