Rispolverando vecchi articoli sull'argomento ([1] e [2]),
vorrei aggiungere una considerazione sull'approccio alla progettazione di questi circuiti.
Noto che nei corsi specializzati su questo argomento vengono enfatizzati metodi di soluzione di logica sequenziale sincrona (Moore, Mealy), ma non si fa alcun cenno a metodi più semplici che pure potrebbero essere utilizzati in problemi pratici di ridotta complessità.
Indice |
Il problema
Per i non iniziati, cominciamo con la distinzione fra logica combinatoria e quella sequenziale.
La logica combinatoria è caratterizzata dal fatto che gli stati delle uscite dipendono univocamente
dagli stati degli ingressi. Ciò significa che ripetendo in qualsiasi momento la combinazione dei degnali d'ingresso, si ha sempre la stessa combinazione dei segnali d'uscita.
Per la logica sequenziale questo non si verifica sempre: alla stessa configurazione degli ingressi possono corrispondere stati diversi delle uscite.
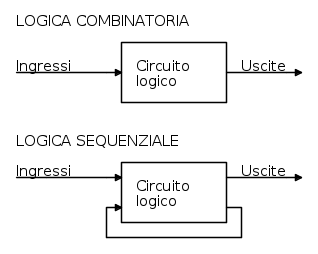
Strutturalmente le due si possono presentare in questo modo:
Come si vede, la differenza è che nella sequenziale, alcune uscite fungono da ulteriori ingressi, e concorrono a determinare lo stato globale delle uscite. In altre parole, lo stato delle uscite dipende dall'evoluzione temporale degli ingressi, cioè dalla "sequenza" con cui questi si presentano.
Ciò ha una immediata conseguenza pratica: non è possibile adottare nel progetto di questa logica i metodi di riduzione utilizzati nella combinatoria, quali ad es. le mappe di Karnaugh.
L'esempio più semplice
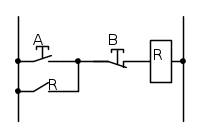
L'esempio più elementare di logica sequenziale è dato dall'autoritenuta di un relè (è la classica soluzione dl comando marcia/arresto di un motore mediante pulsanti):
La chiusura del pulsante A alimenta la bobina del relè R che si automantiene sul proprio contatto R. Per far rilasciare il relè occorre agire sul pulsante (normalmente chiuso) B.
Se ora scriviamo l'espressione booleana corrispondente al circuito:

notiamo quanto evidenziato in precedenza per i circuiti sequenziali: lo stato dell'uscita R dipende anche da sé stessa (dal punto di vista logico possiamo infatti identificare lo stato del contatto con quello della bobina).
L'espressione booleana equivalente è infatti:

che corrisponde alla precedente scambiando S con A, Q con R ed R con B.
La mappa "transizionale"
Si è detto che non è possibile utilizzare per questi circuiti la mappa di Karnaugh, ed infatti è evidente che ad esempio con S ed R entrambi a "0", Q può essere "0" oppure "1" a seconda di ciò che e successo prima!
Se però consideriamo Q come terzo ingresso della mappa, possiamo ragionare sui singoli stati come percorso temporale fra questi.
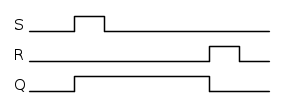
Mettiamo infatti in grafico nel tempo l'evoluzione dei segnali: questa è infatti la miglior "specifica" di quanto deve essere realizzato dal circuito, cioè di cosa vogliamo ottenere.
In base a questa, costruiamo una mappa di Karnaugh relativa a Q, e dipendente dalla variabili S,R e naturalmente la stessa Q.
E' evidente però che ci potranno essere delle discordanze fra lo stato della variabile d'uscita Q e quello dell'ingresso Q: discordanza inammissibile, che quindi deve essere risolta con il passaggio immediato alla condizione di congruenza. Denoteremo questi stati instabili o di transizione racchiudendoli fra parentesi. Per facilitare l'interpretazione del percorso temporale prima citato, indicheremo poi i passaggi con delle freccette.
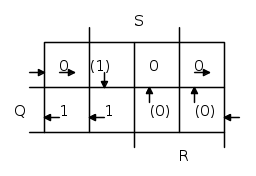
Ecco allora come possiamo riportare nella mappa gli stati del grafico:
Partendo dalla casella in alto a sinistra, si ha la condizione di R,S e Q tutti a "0", che corrisponde all'inizio del grafico temporale. Poi S diventa "1", quindi nella mappa si passa alla casella a destra,
ma il grafico mostra che anche Q deve andare a "1", mentre la casella corrisponde a Q="0". E' dunque uno stato transitorio che trova l'equilibrio nella casella sottostante.
Al termine dell'impulso di S, vi è uno spostamento nella casella a sinistra (e Q rimane stabile ad "1").
Quando interviene R, si ha il passaggio alla casella inferiore a destra, con uno stato transitorio a "0", che lo forza alla casella superiore e, alla fine dell'impulso R, ci si ritrova nella casella di npartenza.
Alla fine del "percorso" rimarrebbero vuote 2 caselle dalla mappa, corrispondenti a S e R entrambi ad "1":
decidiamo di forzare Q a "0", cioè facendo prevalere il Reset sul Set.
Abbiamo così completata la mappa e possiamo ricavare l'espressione di Q: le caselle ad "1" possono essere
raccolte come:

cioè la stessa relazione del SR-FF vista in precedenza.
Un altro esempio
Un'applicazione spesso richiesta è l'emulazione di un relè passo-passo, ottenere cioè una commutazione di un'uscita ad ogni impulso inviato all'ingresso.
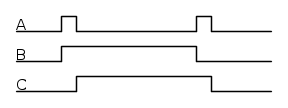
Vi è quindi un segnale d'ingresso (A) ed uno di uscita (B), ma si vede che è necessaria una terza condizione (C), per "memorizzare" il primo impulso. Ecco il relativo grafico nel tempo;
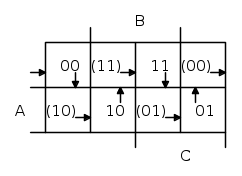
Da questo andamento è possibile ricavare la seguente mappa delle transizioni:
In ogni casella è riportato lo stato delle uscite B,C, racchiudendo tra parentesi, come già detto, gli stati instabili che forzano il passaggio alla casella successiva.
Il "percorso" completo occupa tutte le caselle della mappa e riporta infine alla situazione di partenza
(la prima casella in alto a sinistra)
In effetti la mappa è l'insieme delle due mappe di B (prima cifra) e C (seconda cifra), da cui è possibile ricavare le rispettive espressioni booleane:


Considerazioni
Vantaggio del metodo è la possibilità di risolvere problemi di logica sequenziale con l'impiego di sole porte logiche (nel caso di realizzazioni elettroniche "cablate") o di normali contatti di PLC (che spesso non dispongono di funzioni equivalenti ai FlipFlop).
La semplicità del metodo comporta però alcune limitazioni. Innanzitutto il numero delle variabili: al di là di 4, la mappa diventa ingestibile, ma nella trasposizione pratica in circuito elettronico, ad es.,occorre anche valutare attentamente i tempi di trasporto dei segnali, che possono alterarne il funzionamento.
Vi possono inoltre essere difficoltà di inizializzazione: simulatori del calibro di MicroCap e Multisim vanno in confusione quando si tratta di stabilire stati di dipendenza incrociata (come nel caso dell'ultimo esempio).
In conclusione il metodo, molto usato ai tempi in cui non si disponeva dei componenti sincroni (D-FF,JK-FF,ecc., basati sul clock), è oggi meno diffuso. Ma credo valga la pena di non dimenticarlo.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)