Indice |
Introduzione
In questo secondo articolo si continua l'analisi di possibili soluzioni al problema posto sul forum [1], in cui si chiedeva come convertire un segnale PWM in una tensione continua pari al valor medio del segnale PWM. Nell'articolo precedente [2], si sono analizzate soluzioni basate su filtri RC passivi, filtri che nella maggioranza dei casi sono sufficienti per risolvere il problema.
Benché il problema di passare da segnale PWM a segnale analogico probabilmente non richieda prestazioni così spinte da ricorrere all'uso di un filtro attivo, vale comumque la pena di esaminare anche questa soluzione in confronto con i precedenti filtri passivi  . In realtà questa è solo una scusa per ripassare qualcosa sui filtri attivi.
. In realtà questa è solo una scusa per ripassare qualcosa sui filtri attivi.
Filtri attivi
I filtri attivi, rispetto a quelli visti fino qui, mettono a disposizione del progettista poli complessi coniugati e quindi permettono di realizzare fitri appartenenti alle varie famiglie di filtri classici. Pur usando solo resistori, condensatori e operazionali, permettono di ottenere le stesse funzioni di trasferimento dei filtri passivi classici che però impiegano anche induttori, costosi, voluminosi e con caratteristiche di idealità elettrica non così buone come invece i condensatori. Lo svantaggio dei filtri attivi, oltre al dover usare operazionali, doverli alimentare... risiede nelle limitazioni in frequenza che si possono ottenere con gli operazionali. Esistono numerosissimi libri sui filtri attivi: una prima introduzione la si trova nei capitoli 3 e 4 di questo splendido libro di Sergio Franco [3]. Altri testi più specialistici sono ad esempio il Valkenburg [4], il Deliyannis [5], il Williams [6] e un po' meno approfondito lo Huelsman [7].
Ripassino sui filtri
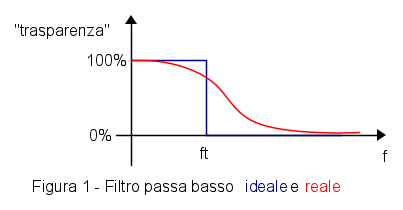
Un filtro ideale passa basso dovrebbe essere totalmente trasparente per tutti i segnali compresi nella sua banda passante, al di sotto della frequenza di taglio  cioè dovrebbe far passare il segnale con attenuazione nulla e fase lineare, mentre dovrebbe bloccare con attenuazione infinita i segnali fuori banda (trasparenza nulla). La transizione fra banda passante e banda bloccata dovrebbe essere un "muro", vedi Figura (1). Purtroppo un filtro del genere non può esistere, anche per motivi teorici, e si è costretti ad approssimare il muro con una funzione realizzabile con componenti elettronici, curva rossa in Figura (1).
cioè dovrebbe far passare il segnale con attenuazione nulla e fase lineare, mentre dovrebbe bloccare con attenuazione infinita i segnali fuori banda (trasparenza nulla). La transizione fra banda passante e banda bloccata dovrebbe essere un "muro", vedi Figura (1). Purtroppo un filtro del genere non può esistere, anche per motivi teorici, e si è costretti ad approssimare il muro con una funzione realizzabile con componenti elettronici, curva rossa in Figura (1).
Queste funzioni realizzabili sono dei polinomi che formano la funzione di trasferimento: a seconda della famiglia scelta di polinomi (Butterworth, Chebysheff...) si ottengono caratteristiche diverse dei filtri. Per molti filtri reali si indica come frequenza di taglio  quella alla quale il guadagno del filtro scende di
quella alla quale il guadagno del filtro scende di  rispetto al valore massimo in banda passante.
rispetto al valore massimo in banda passante.
Non essendo possibile descrivere qui le caratteristiche delle varie famiglie di filtri, in questo caso per nulla critico si sceglierà di usare in prima battuta filtri di Butterworth, che sono dei filtri "tranquilli", con attenuazione che scende in modo monotono, vanno bene per uso generale, ma, come si vedrà, con qualche inconveniente.
Progetto con filtri attivi
Per il progetto di un filtro attivo bisogna specificare questi parametri
- guadagno del filtro in banda passante
- frequenza di taglio
- frequenza della banda attenuata
- attenuazione in banda attenuata
- famiglia del filtro
oltre a una miriade di altri parametri, come la dinamica del segnale, il rumore in uscita, impedenze di ingresso e capacità di pilotaggio dell'uscita, errori ammessi a causa delle tolleranze dei componenti...
In questo caso il guadagno del filtro in banda passante deve essere unitario (già discusso in [2]) e l'attenuazione in banda attenuata, richiesta per avere un ripple in uscita sufficientemente basso, deve essere di almeno  volte alla frequenza di
volte alla frequenza di  .
.
La scelta iniziale della famiglia Butterworth deriva dal volere filtri che non abbiano poli con fattore  troppo elevato per evitare sovraelongazioni e oscillazioni nella risposta al gradino. L'ordine e la frequenza di taglio del filtro verranno discussi nelle due soluzioni presentate.
troppo elevato per evitare sovraelongazioni e oscillazioni nella risposta al gradino. L'ordine e la frequenza di taglio del filtro verranno discussi nelle due soluzioni presentate.
Filtro di ordine assegnato
In questa sezione, al posto di procedere nel modo classico con il progetto, ovvero fissando la frequenza di taglio e l'attenuazione a una data frequenza in banda attenuata, e calcolando poi quale ordine di filtro sia necessario, si seguirà invece una procedura non standard in cui si fissa l'ordine del filtro (secondo) e si accettano la banda passante e il ritardo che ne risultano.
La ragione di questa scelta si basa sulla considerazione che se un filtro passivo con due poli reali soddisfa le specifiche con buone caratteristiche di risposta nel dominio del tempo, usando una cella attiva con due poli complessi coniugati alla stessa frequenza si dovrebbe ottenere una risposta con ancora minore ritardo. La frequenza di taglio  viene scelta in modo da garantire la richiesta di attenuazione a
viene scelta in modo da garantire la richiesta di attenuazione a  .
.
La frequenza di taglio del filtro attivo del secondo ordine è la stessa calcolata in precedenza per i due poli reali coincidenti. La ragione euristica di questa scelta è basata su due aspetti. Il primo è che due poli complessi coniugati sono a tutti gli effetti due poli alla stessa frequenza e se si guarda la banda attenuata, quindi a frequenza abbastanza maggiore dei poli, l'attenuazione che ne risulta è praticamente la stessa dei poli reali poiché a frequenza  , il solo termine importante del denominatore della funzione di trasferimento è quello in
, il solo termine importante del denominatore della funzione di trasferimento è quello in  , che non dipende dalla posizione dei singoli poli.
, che non dipende dalla posizione dei singoli poli.
Si deve quindi progettare un filtro con  e un fattore
e un fattore  dei poli dato dall'approssimazione di Butterworth per il secondo ordine,
dei poli dato dall'approssimazione di Butterworth per il secondo ordine,  . Il guadagno in continua del filtro deve essere unitario. Nei filtri di Butterworth, di qualunque ordine, la frequenza
. Il guadagno in continua del filtro deve essere unitario. Nei filtri di Butterworth, di qualunque ordine, la frequenza  di tutti i poli è la stessa e coincide con la frequenza di taglio
di tutti i poli è la stessa e coincide con la frequenza di taglio  del filtro, mentre varia il fattore
del filtro, mentre varia il fattore  delle varie coppie di poli.
delle varie coppie di poli.
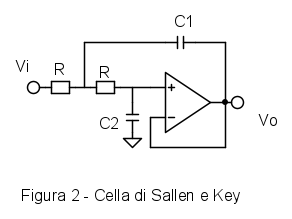
Una struttura che permette di rispettare facilmente queste specifiche è la cella di Sallen e Key costruita intorno al voltage follower [8], che fornisce in continua un guadagno unitario.
La struttura del filtro di Sallen e Key con guadagno unitario è nella Figura (2), in cui si sono poste le due resistenze dello stesso valore, cosa possibile quando il  del filtro è basso.
del filtro è basso.
Il progetto della cella parte scegliendo un valore ragionevole  per le due resistenze uguali e calcolando poi i valori di
per le due resistenze uguali e calcolando poi i valori di  e
e  con queste formule [9]
con queste formule [9]

Se si sceglie ad esempio  , in modo da non caricare troppo la sorgente del segnale PWM, si ottiene per i due condensatori
, in modo da non caricare troppo la sorgente del segnale PWM, si ottiene per i due condensatori


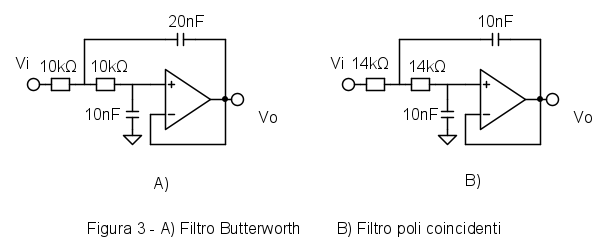
Si noti che se con le resistenze uguali si mettono anche i condensatori di uguale valore, si ottiene un filtro con due poli reali coincidenti, impossibili da realizzare con una rete passiva. Nella Figura (3) sono riportati gli schemi del filtro attivo di Butterworth e della cella che fornisce i due poli reali coincidenti.
Si tenga presente che un sistema con due poli complessi coniugati dà origine a overshoot (sovraelongazione) nella risposta al gradino. Nel caso del secondo ordine la sovraelongazione  può essere calcolata analiticamente in modo abbastanza facile (si trovano le formule sui libri!) [10].
può essere calcolata analiticamente in modo abbastanza facile (si trovano le formule sui libri!) [10].

e per il filtro Butterworth del secondo ordine com  ha una sovraelongazione pari al
ha una sovraelongazione pari al  , che in qualche caso potrebbe non essere accettabile.
, che in qualche caso potrebbe non essere accettabile.
Filtro con banda passante assegnata
I filtri dimensionati nella sezione precedente derivano da un progetto decisamente scadente dal punto di vista ingegneristico poiché non si è tenuto conto delle non idealità e tolleranze dei componenti.
Si è cercato di soddisfare al pelo le specifiche, senza lasciare spazio per le tolleranze dei componenti. Si è anche progettato il filtro in modo non standard, cercando di garantire una specifica attenuazione in banda attenuata e accontentandosi di quello che si aveva per la banda passante.
In generale il filtro viene progettato in funzione di una banda passante e in banda attenuata si ottiene di solito una attenuazione maggiore di quella richiesta.
Per avere margine per le tolleranze dei componenti ma ottenere comunque una banda relativamente elevata e al contempo avere almeno l'attenuazione richiesta, usando ancora una cella del secondo ordine si deve ridurre la frequenza di taglio e aumentare quindi l'attenuazione richiesta a
e aumentare quindi l'attenuazione richiesta a  .
.
Ad esempio se per sicurezza si specificano  di attenuazione a
di attenuazione a  , corrispondenti a una attenuazione di
, corrispondenti a una attenuazione di  volte, il prodotto della frequenza dei due poli complessi deve essere [11] al massimo di
volte, il prodotto della frequenza dei due poli complessi deve essere [11] al massimo di  , perdendo in velocità di risposta.
, perdendo in velocità di risposta.
Un'altra soluzione che sarà esplorata qui prevede di specificare la banda passante e salire con l'ordine del filtro pagando con la complessità circuitale la compensazione degli effetti dei componenti non ideali, senza perdere in banda o attenuazione.
I filtri del terzo ordine sono realizzati con una cella attiva che fornisce i due poli complessi coniugati, ad esempio la Sallen e Key vista prima e una cella  che dà il polo reale. La cella
che dà il polo reale. La cella  che realizza il polo reale va piazzata all'ingresso del filtro, secondO la regola standard di piazzare le celle in ordine crescente di
che realizza il polo reale va piazzata all'ingresso del filtro, secondO la regola standard di piazzare le celle in ordine crescente di  per ridurre le possibilità di saturazione a causa della sovraelongazione delle celle con
per ridurre le possibilità di saturazione a causa della sovraelongazione delle celle con  elevato.
elevato.
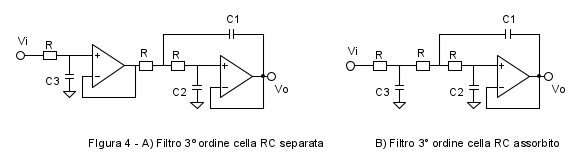
Sono possibili due architetture di filtro, una con la cella  separata da un voltage follower dalla seguente cella attiva, Figura (4A), l'altra invece con la cella
separata da un voltage follower dalla seguente cella attiva, Figura (4A), l'altra invece con la cella  assorbita dalla cella del secondo ordine, come mostrato in Figura (4B).
assorbita dalla cella del secondo ordine, come mostrato in Figura (4B).
Nel caso di cella passiva assorbita nella cella del secondo ordine, l'interazione delle capacità aumenta in modo considerevole le quantità di calcoli da farsi per piazzare correttamente i tre poli. Considerando che lo spazio occupato da un operazionale doppio è praticamente lo stesso di quello di un operazionale semplice (otto piedini), e il costo è quasi lo stesso, nel seguito farò solo i conti per l'architettura con cella  separata, Figura (4A).
separata, Figura (4A).
Con un filtro ideale Butterworth del terzo ordine, sempre per avere una attenuazione di  volte alla frequenza di
volte alla frequenza di  , procedendo come fatto prima, ma tenendo conto che ora la discesa della funzione di trasferimento è di
, procedendo come fatto prima, ma tenendo conto che ora la discesa della funzione di trasferimento è di  potremmo piazzare i tre poli alla frequenza [11]
potremmo piazzare i tre poli alla frequenza [11]
![f_t\approx \frac{20\text{kHz}}{\sqrt[3]{326}}=2.9\,\text{kHz}](/mediawiki/images/math/5/c/c/5ccf77990999f84801bb71a4141704b1.png) .
.
Poiché si vuole un progetto più reale, si riduce la frequenza della banda passante, ad esempio a  circa in modo da avere ancora margine di attenuazione alla frequenza di
circa in modo da avere ancora margine di attenuazione alla frequenza di  .
.
Un progetto potrebbe quindi essere di un filtro Butterworth del terzo ordine con frequenza di taglio di  . Un filtro di ordine dispari ha un polo reale e due poli complessi coniugati, che, come visto prima, purtroppo danno una sovraelongazione nella risposta al gradino. Nel caso di Butterworth del terzo ordine servono tre poli alla frequenza di taglio, uno reale e due complessi coniugati con
. Un filtro di ordine dispari ha un polo reale e due poli complessi coniugati, che, come visto prima, purtroppo danno una sovraelongazione nella risposta al gradino. Nel caso di Butterworth del terzo ordine servono tre poli alla frequenza di taglio, uno reale e due complessi coniugati con  [3], quindi con maggiore overshoot del caso precedente, che risulta essere del
[3], quindi con maggiore overshoot del caso precedente, che risulta essere del  . Questo valore però viene ridotto dal fatto di avere un polo reale che addolcisce il gradino applicato al filtro. Il valore esatto potrebbe essere calcolato analiticamente, ma è più facile ricorrere alla simulazione.
. Questo valore però viene ridotto dal fatto di avere un polo reale che addolcisce il gradino applicato al filtro. Il valore esatto potrebbe essere calcolato analiticamente, ma è più facile ricorrere alla simulazione.
Il calcolo del Butterworth del terzo ordine è semplice: serve un polo reale a  seguito da una cella Sallen e Key con poli complessi coniugati ancora a
seguito da una cella Sallen e Key con poli complessi coniugati ancora a  e fattore
e fattore  . Scegliendo come prima per la cella del secondo ordine due resistori uguali da
. Scegliendo come prima per la cella del secondo ordine due resistori uguali da  e usando le formule già usate in precedenza, si ricava
e usando le formule già usate in precedenza, si ricava


La cella del primo ordine, se si usa ancora lo stesso valore di resistenza, richiede un condensatore  di valore
di valore

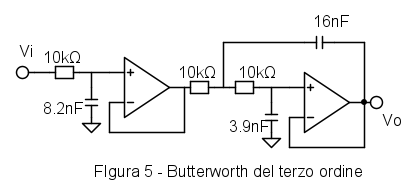
Il risultato del progetto del filtro di Butterworth del terzo ordine è in Figura (5)
Esistono delle famiglie di filtri che danno un overshoot ridotto o quasi inesistente, le principali sono i filtri gaussiani e i filtri di Bessel (da notare che sia Carl Friedrich Gauss sia Friedrich Wilhelm Bessel sono vissuti fra la fine del 1700 e metà del 1800, quando i filtri erano ancora oltre ogni possibile immaginazione. Discorso analgo anche per Pafnuty Chebysheff vissuto nel 1800). I filtri gaussiani hanno sovraelongazione nulla, mentre quelli di Bessel hanno una sovraelongazione molto ridotta.
Poiché non so progettare i filtri gaussiani, non avendo le tabelle delle funzioni a portata di mano, oltre al Butterworth del terzo ordine, si calcolerà anche un filtro di Bessel del terzo ordine con frequenza di taglio anch'esso di  , sperando che rimanga margine in banda attenuata poiché i filtri di Bessel nella transizione fra banda passante e banda attenuata scendono più lentamente e quindi in alta frequenza hanno una attenuazione minore delle altre famiglie di pari ordine.
, sperando che rimanga margine in banda attenuata poiché i filtri di Bessel nella transizione fra banda passante e banda attenuata scendono più lentamente e quindi in alta frequenza hanno una attenuazione minore delle altre famiglie di pari ordine.
Un filtro di Bessel del terzo ordine con banda passante di  , sempre definita a
, sempre definita a  , richiede un polo reale alla frequenza
, richiede un polo reale alla frequenza  e due poli complessi coniugati alla frequenza di
e due poli complessi coniugati alla frequenza di  con un fattore
con un fattore  [3]. Si osservi che il fattore
[3]. Si osservi che il fattore  dei poli del Bessel è minore di quello del Butterworth, e quindi dà una sovraelongazione minore.
dei poli del Bessel è minore di quello del Butterworth, e quindi dà una sovraelongazione minore.
Il progetto del filtro di Bessel procede esattamente come fatto in precedenza: scegliendo per la cella del secondo ordine i soliti due resistori uguali  e usando le formule già usate in precedenza, si ricava
e usando le formule già usate in precedenza, si ricava


La cella del primo ordine, se si usa ancora lo stesso valore di resistenza, richiede un condensatore  di valore
di valore

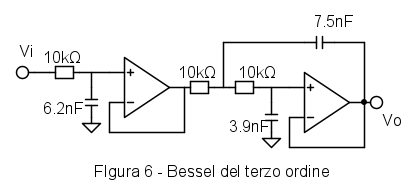
Il risultato del progetto del filtro di Butterworth del terzo ordine è in Figura (6)
Risultati e verifica - Filtri attivi
In questa sezione sono presentate le simulazioni dei circuiti attivi dimensionati in precedenza. Per tutti i filtri saranno presentati, come al solito, l'attenuazione in frequenza, il ripple residuo per il caso più sfavorevole di  e la risposta al gradino, con passaggio da
e la risposta al gradino, con passaggio da  a
a 
Filtri del secondo ordine
Nel grafico di Figura (7) è riportata la simulazione della funzione di trasferimento del filtro di Butterworth del secondo ordine e del filtro con due poli reali coincidenti. Per vedere la figura completa cliccare sull'immagine.
Il filtro di Butterworth, con i poli complessi coniugati alla frequenza di taglio mantiene "elevato" il guadagno e quindi allarga la banda, mentre i due poli reali alla stessa frequenza provocano una attenuazione di  e quindi la banda passante è più stretta. L'attenuazione a
e quindi la banda passante è più stretta. L'attenuazione a  è di
è di  , appena inferiore a quella voluta, a causa della normalizzazione dei condensatori a valori standard più piccoli dei valori calcolati.
, appena inferiore a quella voluta, a causa della normalizzazione dei condensatori a valori standard più piccoli dei valori calcolati.
Il ripple di uscita dei due filtri attivi del secondo ordine è mostrato in Figura (8)
La tensione di ripple picco-picco in uscita è di  , esattamente il valore desiderato, mentre quella dei due poli coincidenti è appena maggiore,
, esattamente il valore desiderato, mentre quella dei due poli coincidenti è appena maggiore,  a causa della normalizzazione effettuata sui componenti.
a causa della normalizzazione effettuata sui componenti.
Infine la (brutta) sorpresa della risposta al gradino, mostrata in Figura (9)
La risposta al gradino del filtro di Butterworth del secondo ordine ha una sovraelongazione del  a causa dei due poli complessi coniugati. Pur non essendo una sovraelongazione di valore elevato, in alcune applicazioni una risposta che vada oltre al valore desiderato potrebbe non essere accettabile. Il tempo di salita al
a causa dei due poli complessi coniugati. Pur non essendo una sovraelongazione di valore elevato, in alcune applicazioni una risposta che vada oltre al valore desiderato potrebbe non essere accettabile. Il tempo di salita al  del valore finale per il filtro di Butterworth è di
del valore finale per il filtro di Butterworth è di  , mentre per il filtro con due poli coincidenti si ha un tempo di salita maggiore, di
, mentre per il filtro con due poli coincidenti si ha un tempo di salita maggiore, di  , e presenta una banda passante più stretta del Butterworth. Si osservi che comunque i due poli reali coincidenti danno un tempo di salita minore dei due poli reali ottenuti con le reti passive
, e presenta una banda passante più stretta del Butterworth. Si osservi che comunque i due poli reali coincidenti danno un tempo di salita minore dei due poli reali ottenuti con le reti passive  , come trovato in [2].
, come trovato in [2].
Filtri del terzo ordine
Le funzioni di trasferimento dei due filtri del terzo ordine (Butterworth e Bessel) con banda passante di  e attenuazione di almeno
e attenuazione di almeno  alla frequenza di
alla frequenza di  sono mostrate in Figura (10). Entrambi i filtri hanno un guadagno di
sono mostrate in Figura (10). Entrambi i filtri hanno un guadagno di  alla frequenza di taglio, ma come si vede dalle curve il filtro di Bessel ha una discesa, che pur essendo sempre di
alla frequenza di taglio, ma come si vede dalle curve il filtro di Bessel ha una discesa, che pur essendo sempre di  , raggiunge la pendenza finale a frequenze maggiori e l'attenuazione pertanto, a pari frequenza, è minore.
, raggiunge la pendenza finale a frequenze maggiori e l'attenuazione pertanto, a pari frequenza, è minore.
La cosa interessante di questi due filtri è il confronto del ritardo di gruppo, rappresentato dalle due curve tratteggiate. Il filtro di Bessel ha un ritardo di gruppo praticamente costante in tutta la banda passante. Questo significa che un segnale composto da tante frequenze (in banda passante) esce dal filtro con una forma inalterata. Invece lo stesso segnale che passa per un filtro di Butterworth ha le sue diverse componenti frequenziali ritardate di fasi e tempi diversi e la forma d'onda all'uscita non ha più la stessa forma dell'ingresso perché le diverse sinusoidi che la compongono arrivano all'uscita con ritardi che dipendono dalla frequenza.
Il ripple di uscita dei due filtri è mostrato in Figura (11). Come c'è da aspettarsi dall'attenuazione dei due filtri a  , le due ondulazioni sono di ampiezza diversa.
, le due ondulazioni sono di ampiezza diversa.
Anche il filtro di Bessel, che ha minore attenuazione, rientra entro le specifiche di ripple di uscita.
Infine in Figura (12) sono presentate le risposte al gradino dei due filtri.
Il filtro di Butterworth ha una sovraelongazione considerevole,  , malgrado la cella del primo ordine smussi il gradino all'ingresso. Anche il filtro di Bessel, avendo poli complessi coniugati, ha sovraelongazione, ma di valore molto ridotto,
, malgrado la cella del primo ordine smussi il gradino all'ingresso. Anche il filtro di Bessel, avendo poli complessi coniugati, ha sovraelongazione, ma di valore molto ridotto,  . Inoltre il filtro di Bessel del terzo ordine ha un tempo di salita più corto rispetto al Butterworth di pari ordine,
. Inoltre il filtro di Bessel del terzo ordine ha un tempo di salita più corto rispetto al Butterworth di pari ordine,  rispetto a
rispetto a  , cosa che a prima vista potrebbe sorprendere. In realtà, se si va a vedere la posizione dei poli dei due filtri, si osserva che il filtro di Bessel ha i poli a frequenza maggiore del filtro di Butterworth, e pertanto è più veloce nella risposta, ma con attenuazione minore ad alta frequenza.
, cosa che a prima vista potrebbe sorprendere. In realtà, se si va a vedere la posizione dei poli dei due filtri, si osserva che il filtro di Bessel ha i poli a frequenza maggiore del filtro di Butterworth, e pertanto è più veloce nella risposta, ma con attenuazione minore ad alta frequenza.
Conclusioni
In questa lunga carrellata, che mi è servita per ripassare i filtri, si è passati da un filtro del primo ordine con tempo di salita di  a un filtro attivo del terzo ordine con tempo di salita di
a un filtro attivo del terzo ordine con tempo di salita di  , quasi trenta volte più veloce, ma parecchio più complicato: le prestazioni si pagano. Qual è il filtro migliore? Per questa specifica applicazione direi un passivo del primo ordine, al più del secondo, ma le possibilità di complicarsi la vita ci sono sempre!
, quasi trenta volte più veloce, ma parecchio più complicato: le prestazioni si pagano. Qual è il filtro migliore? Per questa specifica applicazione direi un passivo del primo ordine, al più del secondo, ma le possibilità di complicarsi la vita ci sono sempre!
Bibliografia
[1] Forum EY, Trasformare PWM in segnale analogico, 19 Gennaio 2021
[2] Isidoro KZ, Conversione PWM -> Tensione I, ElectroYou, Gennaio 2021
[3] S. Franco, Design with Operational Amplifiers and Linear Integrated Circuits, Mg Graw-Hill, 4th ed. 2014.
[4] R. Valkenburg, M. Schauman, H. Xiao, Design of Analog Filters, Oxford University Press, 2nd ed. 2009
[5] T. Deliyannis, Y. Sun, J.K. Fidler, Continuous-Time Active Filter Design, CRC Press 1999
[6] A. Williams, Analog Filter Circuit Design Handbook, McGraw Hill 2013.
[7] L. Huelsman, Active and Passive Analog Filter Design, McGraw Hill 1993
[8] Isidoro KZ, Sensitivity III - Filtri attivi, ElectroYou, Dic. 2010
[9] Maxim Integrated, Minimizing Component-Variation Sensitivity in Single Op Amp Filters, Jul 2002
[10] G. Franklin, J. Powell, A. Emami-Naeini, Feedback Control of Dynamic Systems, Pearson, 8th ed. 2018
[11] Isidoro KZ, Calcoli sui diagrammi di Bode, ElectroYou Feb 2021

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)