Indice |
Introduzione
Dopo aver esaminato le caratteristiche dei sensori NTC [1], in questo articolo vengono descritti i blocchi base che formeranno il termostato, ovvero circuito sensore NTC, comparatore con isteresi e pilotaggio del carico ricavando le equazioni di progetto.
In realta` questo articolo e il successivo sono solo una scusa per fare un po' di elettronica analogica, di quella semplice che so fare anch'io, e per mostrare come si puo` impostare un progetto di un circuito semplice, tenendo conto di qualche fattore che di solito si tende a dimenticare, quali ad esempio le tolleranze dei componenti.
A causa della limitazione della lunghezza articoli, i dettagli del calcolo vero e proprio dei componenti sono mostrati nell'articolo successivo [4]
La temperatura di regolazione sara` assunta fissa o poco variabile ad esempio di  per una incubatrice per uova. Per evitare frequenti azioni di attacca/stacca del riscaldatore o raffreddatore, il termostato ha una isteresi, la cui ampiezza sara` scelta con i vincoli dati dall'applicazione: nell'incubatrice la variazione di temperatura puo` essere solo di qualche frazione di grado Celsius.
per una incubatrice per uova. Per evitare frequenti azioni di attacca/stacca del riscaldatore o raffreddatore, il termostato ha una isteresi, la cui ampiezza sara` scelta con i vincoli dati dall'applicazione: nell'incubatrice la variazione di temperatura puo` essere solo di qualche frazione di grado Celsius.
La frequenza effettiva di accensione e spegnimento dipende, oltre che dall'ampiezza dell'isteresi, anche dalle caratteristiche termiche del sistema controllato, e non puo` essere calcolata a meno di non conoscere il modello termico del sistema.
Nel prossimo articolo di progetto vero e proprio si considerera` una temperatura variabile in un intervallo di circa  , mostrando come questa specifica cambia il progetto.
, mostrando come questa specifica cambia il progetto.
Ingredienti
Il termostato che si vuole dimensionare e` formato da tre blocchi principali:
- Circuito NTC per il sensing della temperatura
- Comparatore con isteresi per rivelare quando la temperatura raggiunge i valori prefissati
- Driver di uscita per pilotare il rele'.
Di seguito saranno analizzati in dettaglio questi tre blocchi, enfatizzando l'aspetto teorico generale. Dato che troppa teoria impasta la bocca come il burro di arachidi, meglio diluire anche con qualche esempio numerico.
Circuito NTC
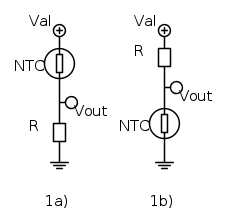
Il circuito piu` semplice che, usando una NTC, permette di ricavare una tensione funzione della temperatura e` un semplice partitore di tensione collegato all'alimentazione, come mostrato in figura.
La versione 1a) fornisce in uscita una tensione che aumenta con l'aumentare della temperatura, mentre il circuito 1b) da` una tensione che diminuisce all'aumentare della temperatura.
I criteri di dimensionamento di questa sezione riguardano la scelta del valore dell'NTC  e della resistenza
e della resistenza  . Serve anche conoscere come varia la tensione di uscita del partitore al variare della temperatura ed eventualmente l'impedenza equivalente vista guardando dentro il partitore.
. Serve anche conoscere come varia la tensione di uscita del partitore al variare della temperatura ed eventualmente l'impedenza equivalente vista guardando dentro il partitore.
Il problema della scelta di  rispetto a
rispetto a  per ottenere una tensione il piu` lineare possibile con la temperatura sara` trattata diffusamente nel quarto articolo della serie. In questo progetto serve solo poter mantenere costante una temperatura praticamente fissa, dettata dall'applicazione e quindi la linearita` di
per ottenere una tensione il piu` lineare possibile con la temperatura sara` trattata diffusamente nel quarto articolo della serie. In questo progetto serve solo poter mantenere costante una temperatura praticamente fissa, dettata dall'applicazione e quindi la linearita` di  in funzione di
in funzione di  non e` importante.
non e` importante.
Il parametro che invece potrebbe essere conveniente massimizzare e` la variazione di  al variare di
al variare di  , cioe` la variazione del rapporto di partizione rispetto alla temperatura.
, cioe` la variazione del rapporto di partizione rispetto alla temperatura.
Massimizzare la variazione di tensione di uscita con la temperatura richiede qualche derivata, qui riportata per i masochisti. Tutti gli altri possono saltare direttamente alla fine del paragrafo dove c'e` il risultato pratico importante.
Il rapporto di partizione  per il circuito 1a) e` dato da
per il circuito 1a) e` dato da

dove il valore dell'NTC e` espresso per comodita` in funzione di  , ma i risultati pratici saranno espressi in termini della resistenza nominale
, ma i risultati pratici saranno espressi in termini della resistenza nominale  . Si e` anche messo in evidenza
. Si e` anche messo in evidenza  che viene inglobata nel parametro
che viene inglobata nel parametro  .
.
La variazione del rapporto di partizione in funzione della temperatura e` dato dalla derivata dell'espressione:

Per massimizzare questo rapporto intorno a una qualunque temperatura di lavoro  (che in questa applicazione e` praticamente fissa) bisogna ancora derivare l'espressione (2) rispetto a
(che in questa applicazione e` praticamente fissa) bisogna ancora derivare l'espressione (2) rispetto a  , il nostro grado di liberta` e poi uguagliare a zero la derivata. Questa massimizzazione non riguarda la linearita`, ma solo la sensibilita`. La derivata risulta essere:
, il nostro grado di liberta` e poi uguagliare a zero la derivata. Questa massimizzazione non riguarda la linearita`, ma solo la sensibilita`. La derivata risulta essere:

Il valore di  che annulla la derivata (3) e`
che annulla la derivata (3) e`

e ricordando che dentro  e` nascosta il valore della resistenza
e` nascosta il valore della resistenza  si ha:
si ha:

E questo e` il risultato importante: per massimizzare la sensibilita` del circuito ad una data temperatura bisogna scegliere una resistenza di partizione  uguale alla resistenza che ha l'NTC a quella temperatura.
uguale alla resistenza che ha l'NTC a quella temperatura.
Se si effettua questa scelta, la variazione del rapporto di partizione al variare della temperatura risulta essere pari a

dove il parametro  e` la sensibilita` dell'NTC definita in eq. (11) di [1].
e` la sensibilita` dell'NTC definita in eq. (11) di [1].
Verifichiamo che questa sensibilita` sia sufficiente, ovvero che la variazione di tensione di uscita  al variare della temperatura sia facilmente utilizzabile. La variazione di tensione di uscita intorno al punto ottimo vale:
al variare della temperatura sia facilmente utilizzabile. La variazione di tensione di uscita intorno al punto ottimo vale:

e questa variazione di tensione e` ottenuta rispetto a una tensione continua di meta` della tensione di alimentazione.
Usando come dati l'NTC del precedente articolo [1] ( e con
e con  ) e di lavorare a
) e di lavorare a  si ha una resistenza dell'NTC pari a
si ha una resistenza dell'NTC pari a

che e` anche il valore della resistenza  da utilizzare.
da utilizzare.
Lavorando con tensione di alimentazione di  la sensibilita` del circuito diventa, dalla formula (7)
la sensibilita` del circuito diventa, dalla formula (7)

Questa sensibilita` e maggiore di oltre un ordine di grandezza di quella di un sensore allo stato solido, come l'LM35. Lo svantaggio e` la non linearita` della funzione quando ci si allontana dal punto di funzionamento calcolato.
Il valore di partizione ottimo e` 1/2 e la tensione di uscita dal partitore alla quale si ha il punto di ottimo e`  ,
Con la resistenza ottima
,
Con la resistenza ottima  , la tensione di uscita del partitore in condizioni nominali e` di
, la tensione di uscita del partitore in condizioni nominali e` di  , valore adatto al range di modo comune di qualunque operazionale, anche non single supply, usato ad alimentazione singola. Il valore di
, valore adatto al range di modo comune di qualunque operazionale, anche non single supply, usato ad alimentazione singola. Il valore di  deve pero` essere scelto fra quelli normalizzati, cioe`
deve pero` essere scelto fra quelli normalizzati, cioe`  , oppure
, oppure  .
.
Con questa scelta di resistenze il valore nominale di tensione all'uscita del partitore e` di circa  oppure
oppure  , ed e` ancora praticamente a meta` della tensione di alimentazione: il segnale proveniente dall'NTC puo` essere collegato direttamente all'ingresso di qualunque operazionale senza rischiare di portarlo al di fuori dell'intervallo ammissibile delle tensioni di ingresso.
, ed e` ancora praticamente a meta` della tensione di alimentazione: il segnale proveniente dall'NTC puo` essere collegato direttamente all'ingresso di qualunque operazionale senza rischiare di portarlo al di fuori dell'intervallo ammissibile delle tensioni di ingresso.
Anche una variazione di  fa variare la tensione proveniente dal sensore di circa un paio di volt, e si rimane sempre nell'intervallo delle tensioni di modo comune per praticamente qualunque operazionale.
fa variare la tensione proveniente dal sensore di circa un paio di volt, e si rimane sempre nell'intervallo delle tensioni di modo comune per praticamente qualunque operazionale.
I valori della sensibilita` alla temperatura nominale, calcolati con (2) e (7) per i due valori di resistenze normalizzate di  e
e  , e per il valore ideale di resistenza e` dato nella seguente tabella, insieme con il valore di tensione nominale di uscita.
, e per il valore ideale di resistenza e` dato nella seguente tabella, insieme con il valore di tensione nominale di uscita.
| Resistenza | Sensibilita` | Variaz % sensib. |  nominale nominale
|
|---|---|---|---|
 |  |  | 
|
 |  |  | 
|
 |  |  | 
|
Tutte queste cifre decimali sulla sensibilita` non sono solo inutili, sono anche ingegneristicamente sbagliate, ma servono a mostrare l'esiguita` della variazione della sensibilita` con la variazione della resistenza  .
.
La resistenza equivalente del partitore e` data dal parallelo  e in questo esempio e` di circa
e in questo esempio e` di circa  e di
e di 
L'ultimo punto da verificare e` l'autoriscaldamento del sensore dovuto alla corrente che lo attraversa. Usando la resistenza piu` piccola, che da` il caso peggiore alla temperatura nominale, si ha che la potenza massima dissipata dall'NTC vale:
 .
.
Se invece si vuole trovare la massima potenza dissipata su un intervallo di temperatura, il caso peggiore si ha quando la resistenza dell'NTC e` uguale alla resistenza  (adattamento energetico con carico variabile), e la potenza dissipata vale
(adattamento energetico con carico variabile), e la potenza dissipata vale
 .
.
La differenza e` praticamente nulla perche' la resistenza scelta e` vicina al valore ottimo. Questa differenza non e` una pignoleria, e` tempo perso!, ma finche' non si fa il conto almeno una volta non e` facile saperlo a priori.
L'aumento di temperatura dovuto all'autoriscaldamento dipende dalla conduttanza termica del componente. Con l'NTC esaminata in [1], avente in aria ferma un Dissipation Factor [2]  si ha un autoriscaldamento di
si ha un autoriscaldamento di

Questo e` un errore che per alcune applicazioni potrebbe essere troppo elevato. Se il valore dell'NTC fosse piu` basso, ad esempio  , la potenza dissipata, a pari tensione e criterio di progetto, e l'autoriscaldamento salirebbero di circa un fattore 10: un autoriscaldamento di
, la potenza dissipata, a pari tensione e criterio di progetto, e l'autoriscaldamento salirebbero di circa un fattore 10: un autoriscaldamento di  e` molto spesso non accettabile. Queste considerazioni indicano che e` opportuno scegliere valori non troppo bassi per il sensore.
e` molto spesso non accettabile. Queste considerazioni indicano che e` opportuno scegliere valori non troppo bassi per il sensore.
L'errore effettivo e` piu` basso se l'NTC non e` in aria ferma ma c'e` una ventola che fa circolare l'aria, oppure se il sensore e` fissato con pasta termoconduttiva su una superficie a bassa resistenza termica. In caso contrario per ridurre la potenza dissipata e quindi l'autoriscaldamento si puo` aumentare il valore nominale dell'NTC, oppure aumentare solo il valore della resistenza in serie. In quest'ultimo caso la sensibilita` scende e anche la tensione a riposo all'uscita del partitore si avvicina al limite delle tensioni di modo comune dell'operazionale.
Se il non flusso di aria intorno all'NTC non varia, si potrebbe compensare l'autoriscaldamento con la taratura, ma non e` una soluzione da usarsi se non in casi disperati: un cambiamento del flusso d'aria puo` cambiare drasticamente il punto di regolazione.
Comparatore con isteresi
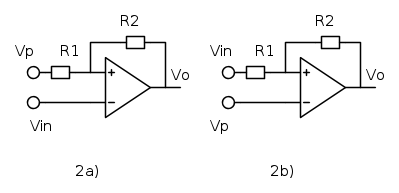
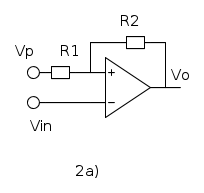
Il circuito del comparatore con isteresi e` quello straclassico riportato in figura, sia per la versione invertente 2a) che non invertente 2b). Una analisi interattiva di questo circuito, preparata da Giovanni Schgoer, e` disponibile in [3].
La tensione  e` una tensione continua di riferimento, derivata dall'alimentazione e serve a posizionare il livello delle soglie. Nello schema 2a) la tensione
e` una tensione continua di riferimento, derivata dall'alimentazione e serve a posizionare il livello delle soglie. Nello schema 2a) la tensione  e
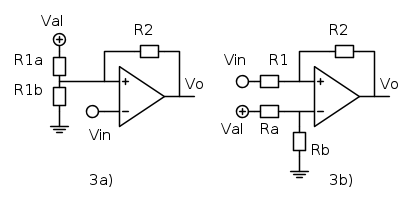
e  possono essere considerate un equivalente Thevenin di
possono essere considerate un equivalente Thevenin di  e
e  , come mostrato nello schema 3a), mentre per il circuito 3b) la tensione
, come mostrato nello schema 3a), mentre per il circuito 3b) la tensione  e` ottenuta con un semplice partitore formato da
e` ottenuta con un semplice partitore formato da  e
e  .
.
Il circuito attivo puo` essere un comparatore di tensione oppure anche un operazionale. In questo caso non avendo la necessita` di velocita` elevate di commutazione e` possibile usare un operazionale, che tipicamente ha uno slew rate minore di un comparatore, ma ha come vantaggio il "risparmio" di una resistenza di pull-up che invece e` necessaria nei comparatori.
Poiche` si e` a singola alimentazione e dovremo fornire in uscita un segnale riferito al negativo, e` molto opportuno utilizzare un operazionale la cui uscita possa scendere fino alla tensione di alimentazione negativa, tipo l'LM358, oppure qualunque altro operazionale single supply.
La tensione di modo comune di ingresso con il circuito dell'NTC visto prima non deve necessariamente scendere fino al negativo o salire fino al positivo, dato che si lavora con tensioni di ingresso circa a meta` della tensione di alimentazione, ma anche un ingresso di tipo single supply o rail to rail non da` problemi.
Calcolo delle soglie e dell'isteresi
Le regole per analizzare il comportamento di un circuito con un comparatore sono molto semplici:
- La tensione di uscita
 e` quasi sempre satura, schiantata contro il massimo valore verso l'alimentazione positiva
e` quasi sempre satura, schiantata contro il massimo valore verso l'alimentazione positiva  o il minimo valore verso l'alimentazione negativa
o il minimo valore verso l'alimentazione negativa 
- Le tensioni sui morsetti invertente
 e non invertente
e non invertente  vanno dove vogliono, non sono vincolate fra di loro.
vanno dove vogliono, non sono vincolate fra di loro.
- Quando le tensioni
 e
e  si incrociano, cioe` diventano uguali, la tensione di uscita passa da una saturazione all'altra, e in quel momento gli ingressi non consumano corrente
si incrociano, cioe` diventano uguali, la tensione di uscita passa da una saturazione all'altra, e in quel momento gli ingressi non consumano corrente
A dire il vero gli ingressi non consumano corrente quasi mai, ma a me piace di piu` detta come sopra.
Il calcolo delle due tensioni di soglia di un comparatore con isteresi e` semplice: basta trovare il valore di tensione di ingresso  che rende uguali i valori delle tensioni di ingresso del comparatore
che rende uguali i valori delle tensioni di ingresso del comparatore  . Queste due tensioni di ingresso che fanno scattare il comparatore si indicano con
. Queste due tensioni di ingresso che fanno scattare il comparatore si indicano con  e
e  e la loro differenza e` l'ampiezza dell'isteresi:
e la loro differenza e` l'ampiezza dell'isteresi:  .
.
Comparatore Invertente
Nel caso del comparatore invertente, riportato qui per comodita`
le condizioni di uguaglianza delle due tensioni  e
e  sono
sono

Se le due tensioni sono uguali si ha l'ingresso al valore della soglia e quindi

dove  e` la soglia superiore, piu` positiva, e
e` la soglia superiore, piu` positiva, e  e` quella inferiore. L'ampiezza dell'isteresi e` data da
e` quella inferiore. L'ampiezza dell'isteresi e` data da

where  is the op amp output voltage swing. Per operazionali single supply, come ad esempio l'LM358, la tensione minima e` praticamente pari alla tensione negativa di alimentazione che e` presa come riferimento, quindi
is the op amp output voltage swing. Per operazionali single supply, come ad esempio l'LM358, la tensione minima e` praticamente pari alla tensione negativa di alimentazione che e` presa come riferimento, quindi  mentre la tensione massima positiva, tranne che negli operazionali rail-to-rail, rimane circa
mentre la tensione massima positiva, tranne che negli operazionali rail-to-rail, rimane circa  al di sotto della tensione di alimentazione:
al di sotto della tensione di alimentazione:  Da notare che il valore esatto dipende dall'operazionale, dalle condizioni di funzionamento e dal carico sull'uscita.
Da notare che il valore esatto dipende dall'operazionale, dalle condizioni di funzionamento e dal carico sull'uscita.
Il valore della tensione media fra le due soglie, che per piccole isteresi puo` essere considerata come "soglia media"  sulla quale e` aggiunta l'isteresi indicata prima, vale
sulla quale e` aggiunta l'isteresi indicata prima, vale

Conoscendo la variazione di tensione di uscita dell'operazionale e l'ampiezza dell'isteresi si puo` calcolare il rapporto delle resistenze per il comparatore invertente con isteresi:

Il valore di  , dopo un po' di algebra, risulta pari a
, dopo un po' di algebra, risulta pari a
 oppure
oppure

Se si tiene conto del fatto che  e quindi che
e quindi che  il valore di
il valore di  si semplifica in questo modo:
si semplifica in questo modo:


Si hanno cosi` le due equazioni (17) e (18) o (19) che permettono di calcolare per il comparatore invertente con isteresi il rapporto delle resistenze e la tensione  . Il valore effettivo delle resistenze va scelto, se non ci sono altri vincoli, con il solito buon senso: non troppo grandi per non essere suscettibili al rumore e alle correnti di polarizzazione dell'integrato, non troppo piccole per non caricare troppo l'uscita dell'integrato e il resto del circuito.
. Il valore effettivo delle resistenze va scelto, se non ci sono altri vincoli, con il solito buon senso: non troppo grandi per non essere suscettibili al rumore e alle correnti di polarizzazione dell'integrato, non troppo piccole per non caricare troppo l'uscita dell'integrato e il resto del circuito.
Comparatore non invertente
Il comparatore non invertente il cui schema e` riportato qui di seguito,
lo si analizza con la stessa procedura, cambia solo un po' la forma delle equazioni.
L'equazione iniziale, analoga alla (13) dell'invertente, e`

e i valori di tensione di ingresso che rendono vera questa uguaglianza sono i valori di soglia. Al solito  puo` assumere solo il valore massimo o minimo, essendo l'uscita sempre in saturazione, tranne durante la commutazione.
puo` assumere solo il valore massimo o minimo, essendo l'uscita sempre in saturazione, tranne durante la commutazione.
I calcoli sono analoghi al caso precedente, si riportano qui solo i risultati finali:

 oppure
oppure

Il legame fra isteresi di temperatura  ed isteresi elettrica
ed isteresi elettrica  per entrambi i comparatori e` ottenuto dall'equazione (7)
per entrambi i comparatori e` ottenuto dall'equazione (7)

Interfacciamento carico
Questa e` la parte facile :) Tipicamente il termostato deve pilotare un rele' e quindi bisogna interfacciare un carico che assorbe una corrente relativamente elevata all'uscita di un operazionale in grado di fornire tipicamente una decina di milliampere.
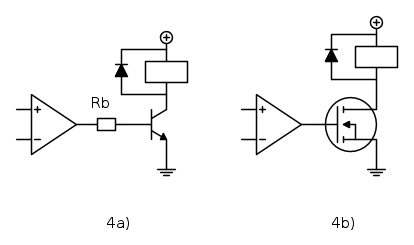
Gli schemi possibili utilizzano un transistore bipolare oppure un mos, come mostrato in figura.
Lo schema in figura 4a ha lo svantaggio di una corrente di base limitata dall'operazionale. Usando un normale operazionale la massima corrente erogabile e` dell'ordine di  a temperatura ambiente con una tensione di uscita tipicamente di circa
a temperatura ambiente con una tensione di uscita tipicamente di circa  piu` bassa della tensione di alimentazione. Con temperature diverse da
piu` bassa della tensione di alimentazione. Con temperature diverse da  e fino a tutto l'intervallo a cui puo` funzionare il componente, la massima corrente garantita tipicamente si riduce a
e fino a tutto l'intervallo a cui puo` funzionare il componente, la massima corrente garantita tipicamente si riduce a  .
.
In caso di alimentazione a  la tensione di uscita alta sara` di circa
la tensione di uscita alta sara` di circa  e quindi la resistenza di base va calcolata come
e quindi la resistenza di base va calcolata come

Da notare che in caso di alimentazione a  la tensione di uscita si riduce a
la tensione di uscita si riduce a  circa, e non e` garantito che l'operazionale possa erogare
circa, e non e` garantito che l'operazionale possa erogare  .
.
Un transistore in saturazione viene tipicamente fatto lavorare con  e questo significa che la massima corrente di carico e` di circa
e questo significa che la massima corrente di carico e` di circa  .
.
Se il carico necessita di correnti piu` elevate si passa al circuito 4b, che utilizza un mos di potenza. I normali mos necessitano per accendersi correttamente di una tensione gate-source di almeno  , proprio quello che viene fornito dall'operazionale. Di solito in serie al gate dei mos di potenza e` inserita una resistenza con lo scopo di smorzare risonanze fra capacita` di ingresso del mos e induttanza dei collegamenti. In questo caso non e` necessaria perche' lo smorzamento e` fornito dalla relativamente elevata impedenza di uscita dell'operazionale e dalla sua limitata corrente erogabile.
L'operazionale in questo circuito non e` usato come amplificatore lineare e quindi un elevato carico capacitivo non pregiudica la sua stabilita`.
, proprio quello che viene fornito dall'operazionale. Di solito in serie al gate dei mos di potenza e` inserita una resistenza con lo scopo di smorzare risonanze fra capacita` di ingresso del mos e induttanza dei collegamenti. In questo caso non e` necessaria perche' lo smorzamento e` fornito dalla relativamente elevata impedenza di uscita dell'operazionale e dalla sua limitata corrente erogabile.
L'operazionale in questo circuito non e` usato come amplificatore lineare e quindi un elevato carico capacitivo non pregiudica la sua stabilita`.
La resistenza  del mos va scelta in modo che quando scorre la corrente nominale di carico, in questo caso il rele`,
del mos va scelta in modo che quando scorre la corrente nominale di carico, in questo caso il rele`,  , la caduta di tensione ai capi del mos sia trascurabile rispetto alla tensione di alimentazione.
, la caduta di tensione ai capi del mos sia trascurabile rispetto alla tensione di alimentazione.
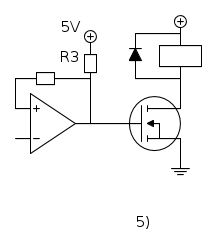
Con l'alimentazione a  bisogna usare un mos logic-level, e comunque la tensione di uscita di
bisogna usare un mos logic-level, e comunque la tensione di uscita di  potrebbe essere ancora troppo bassa per accendere correttamente il mos. In questo caso e` necessario usare una resistenza di pull-up per aumentare la tensione di uscita a livello alto, come mostrato in figura 5.
potrebbe essere ancora troppo bassa per accendere correttamente il mos. In questo caso e` necessario usare una resistenza di pull-up per aumentare la tensione di uscita a livello alto, come mostrato in figura 5.
La scelta della resistenza di pull-up  puo` essere fatta in modo sicuro solo usando un comparatore, per il quale e` specificato quanta corrente viene assorbita dall'uscita con un livello alto: questo parametro e` chiamato nei datasheet "Output Leakage Current" e, insieme con la corrente assorbita da
puo` essere fatta in modo sicuro solo usando un comparatore, per il quale e` specificato quanta corrente viene assorbita dall'uscita con un livello alto: questo parametro e` chiamato nei datasheet "Output Leakage Current" e, insieme con la corrente assorbita da  permette di conoscere la corrente che scorre in questa resistenza e quindi calcolarne il valore per garantire la tensione di uscita voluta a livello alto.
permette di conoscere la corrente che scorre in questa resistenza e quindi calcolarne il valore per garantire la tensione di uscita voluta a livello alto.
Nel caso di un operazionale invece questo parametro non e` indicato. Mettendo una resistenza di pull-up analoga a quella di un comparatore dello stesso tipo (ad esempio LM358-LM393) si ottiene un risultato quasi sempre buono, ma tutto questo non e` garantito. Il che significa che in caso di progetto con standard elevati come ad esempio militare, life support in cui bisogna giustificare in modo inattaccabile ogni singola scelta, non si puo` usare un operazionale e si deve andare su un comparatore. In caso di progetto consumer o a maggior ragione hobbistico, un operazionale con resistenza di pull-up e` accettabile.
Da tenere presente che questa tensione a livello alto e` anche quella usata dalla rete di retroazione positiva per creare l'isteresi e la resistenza di feedback carica l'uscita.
I rele` allo stato solido sono una buona alternativa al rele` elettromeccanico. In questo caso il loro ingresso e` un led con una resistenza in serie, e puo` essere collegato direttamente all'operazionale.
Soluzioni che prevedono l'uso di configurazioni Darlington non sono normalmente utili, poiche' a fronte di un guadagno di corrente maggiore che nel bjt, si ha una caduta di tensione sul Darlington dell'ordine di oltre un volt, mentre con un mos questa caduta di tensione puo` essere ridotta a valori molto piu` piccoli.
Conclusioni
In questo articolo si sono analizzati i blocchi base per la costruzione del termostato. Il circuito con l'NTC e` un semplice partitore, in cui per massimizzare la sensibilita` alle variazioni di temperatura conviene che il valore della resistenza in serie sia pari a quella dell'NTC.
Il comparatore e` il classico comparatore con isteresi, per il quale si e` fatto un ripasso ricavando le formule di progetto. Infine si e` analizzato l'interfacciamento al carico con transistore bipolare o MOS. Nel prossimo articolo saranno fatti i conti veri e propri per il progetto di uno specifico circuito, tenendo anche conto di alcune tolleranze dei componenti.
Bibliografia
[1] Isidoro KZ, Progetto Termostato I - Proprieta` delle NTC - ElectroYou Sett. 2011
[2] NTC Vishay, serie NTCLE100
[3] Gschgor, Comparatore con isteresi - Electroyou 2008
[4] Isidoro KZ, Progetto Termostato-III-Dimensionamento e Calcoli Electroyou Sett 2011.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)