È ormai passata una vita dalla prima parte dell'articolo, che potete leggere qui. Per riassumere brevemente, sto trattando la progettazione di un convertitore DC-DC chiamato active clamp forward per ottenere 5 V, con isolamento, da una tensione di ingresso che varia in un ampio range. Nella prima parte ho introdotto la conversione dell'energia DC-DC e descritto il dimensionamento del trasformatore per questa topologia.
Quest'ultima parte include la progettazione di tutto il convertitore, ossia la selezione dei dispositivi di potenza, il dispositivo di controllo e rettifica, il dimensionamento del feedback e la realizzazione del prototipo. Infine, sono inclusi i risultati delle misure in laboratorio: waveforms, termiche ed efficienza.
Indice |
Topologia
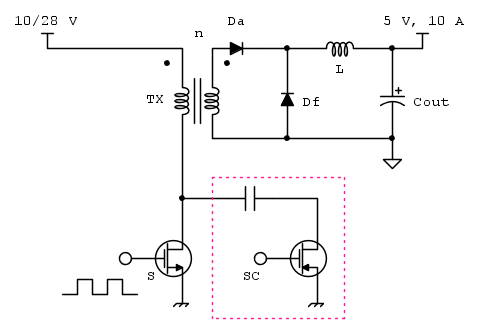
La topologia dell'active clamp forward è riportata di seguito; per una sua descrizione dettagliata rimando alla prima parte dell'articolo, mentre qui ne farò un piccolo riassunto.
In sintesi, il convertitore è la versione isolata di un buck. Il MOSFET S, al primario, alimenta il trasformatore durante la sua accensione. Al secondario si instaura, durante l'accensione di S, una tensione pari a  , dove n = Ns / Np è il rapporto di trasformazione di TX. Il secondario è composto da due dispositivi di rettifica che alimentato l'induttore L: quando S è attivo Da è in conduzione, mentre Df conduce nella fase duale (fino a che la corrente in L non arriva a zero). Df è il famoso diodo di freewheeling.
, dove n = Ns / Np è il rapporto di trasformazione di TX. Il secondario è composto da due dispositivi di rettifica che alimentato l'induttore L: quando S è attivo Da è in conduzione, mentre Df conduce nella fase duale (fino a che la corrente in L non arriva a zero). Df è il famoso diodo di freewheeling.
Il trasformatore, dotato dei suoi parassiti, chiede di essere resettato: in particolare, come spiegato dettagliatamente nella prima parte dell'articolo, la sua corrente di magnetizzazione e l'energia nella leakage vengono riciclate in una rete di clamp. Nei convertitore più semplici queste energie sono dissipate durante ogni ciclo da uno snubber dissipativo.
All'interno della linea tratteggiata è evidenziata la rete di clamp, formata da un PMOS e da un condensatore. Questa rete è anche chiamata low-side clamp, perché il condensatore è collegato tra il nodo di phase (il drain di S) e gli 0 V. Esiste anche l'high-side clamp, dove il condensatore viene collegato tra phase e tensione di alimentazione come i comuni snubber dissipativi. Le due modalità differiscono, oltre che per la modalità di collegamento, per la tensione che la capacità di clamp deve sopportare (che è funzione del DC) e che quindi influisce sul dimensionamento del MOSFET S (datasheet LT3753, pag. 21).
La tensione sulla capacità, infatti, deve essere sopportata dal canale di S quando questo è spento: con il low-side clamp si può scegliere S a rating di tensione minore, ottenendo migliori performance in termini di efficienza a parità di area occupata.
Specifiche
Il range di tensione di ingresso è stato ampliato rispetto a quanto introdotto nella prima parte. Anche la frequenza di switching è stata aumentata dopo alcuni test di laboratorio, e i parametri del trasformatore di conseguenza: tutti i risultati della parte precedente rimangono comunque validi.
Conversione
Vin,min = 10 V
Vin,max = 28 V
Vout = 5 V
Iout,max = 10 A
fsw = 150 kHz
Trasformatore
Core: RM10, N87, ungapped
Np = 8
Ns = 6
Principio di controllo
Se sembro frettoloso, rimando alla prima parte dell'articolo.
Il punto di partenza: la tensione di uscita deve essere stabile.
Collegando e scollegando carichi la variazione dell'uscita deve rimanere entro limiti predefiniti, e non è ammissibile che a regime Vout non sia uguale a 5 V. Perciò, quando la tensione di uscita cala, il duty-cycle va prontamente incrementato per ripristinarla, e viceversa va diminuito quando cresce sopra il riferimento. Scrivendo il rapporto di trasformazione di qualsiasi convertitore a commutazione potrebbe sembrare sufficiente fissare un certo DC per avere una tensione stabile in uscita: questo non è certamente vero nella realtà dove i convertitori non sono ideali, la tensione di ingresso è ampiamente variabile e vanno considerati i fenomeni dissipativi, le dinamiche durante i transitori di carico e le non idealità di tutta la struttura. In genere, perturbando l'uscita di un convertitore che esce con un LC a DC fisso, si osserverà un transitorio oscillatorio smorzato che può durare svariati millisecondi e modificare Vout di svariati volt. Per questo motivo la regolazione della tensione di uscita, nella quasi totalità delle conversioni DC-DC, è imprescindibile (voglio vedere se avete il coraggio di attaccare un microcontrollore a un convertitore a commutazione non regolato).
Il convertitore può essere (principalmente) controllato in due modi: in duty-cycle (aka in tensione) o in corrente. Le due soluzioni differiscono profondamente, così come la funzione di trasferimento del convertitore che ne risulta. Il controllo in tensione genera un duty-cycle in base all'errore sulla tensione di uscita, mentre il controllo in corrente impone una corrente di induttore in base all'errore sulla tensione di uscita. Quest'ultima tecnica è la più classica e si trova in quasi tutti gli alimentatori, e ha come palese vantaggio quello di fornire al circuito di controllo l'informazione sulla corrente reale che circola su L. Questo permette di implementare misure di sicurezza che il controllo in tensione non ha, quali ad esempio la limitazione della corrente stessa e la sicurezza che l'induttore non saturi mai. Di contro, la corrente va rilevata ciclo per ciclo.
Visto che nel nostro caso si utilizzerà un controllo di corrente, tratterò solo questo. Ciò non toglie che online si trovino abbondanti informazioni su entrambi i metodi.
Controllo di corrente di picco
Per implementare il controllo in corrente si possono seguire varie strade, per esempio utilizzando la misura della corrente media, il picco o la valley. Queste tecniche sono utilizzate anche nelle versioni non isolate, ma più raramente (poi dipende dall'ambito di applicazione), dove la misura di corrente è effettuata direttamente sull'induttore attraverso una resistenza in serie o attraverso il DCR sensing (utilizzando la resistenza parassita dell'induttore, quindi senza aggiungere ulteriori fonti di perdita).
Per i convertitori isolati la misura di corrente avviene quasi sempre al primario, attraverso una resistenza di sensing (shunt) riferita agli 0 V, o alternativamente con un trasformatore di corrente a monte del trasformatore quando le correnti in gioco sono più grandi. La misura al primario è comoda perché, in genere, il controllore si trova sul lato primario e non serve trasportare informazioni attraverso l'isolamento. La corrente misurata durante l'accensione del MOSFET S è infatti -quasi- una copia della corrente sull'induttore, scalata per il rapporto di trasformazione.
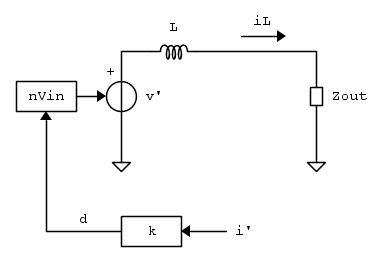
Il circuito equivalente durante l'accensione di S, con annessa la resistenza di sensing al primario, è il seguente (le waveforms in blu corrispondono a questo sotto-periodo):
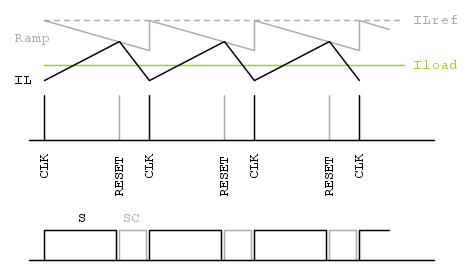
Nel caso in esame il controllore impone il picco di corrente su L misurandola durante l'accensione di S: questa modalità è chiamata peak current mode, o controllo di corrente di picco. In questo modo il convertitore si comporta come un generatore di corrente controllato (entro certi limiti e con una certa dinamica che vedremo dopo): quando la tensione di uscita scende, il picco di corrente viene alzato per ritornare alla tensione di riferimento, viceversa viene abbassato quando la tensione di uscita è troppo alta. Il modo più classico per imporre questo comportamento è utilizzare un clock a frequenza costante per accendere S, e spegnerlo quando il picco viene raggiunto, come in figura:
Nello schema è mostrata anche la tecnica di slope compensation: al riferimento di corrente ILref viene sottratto un segnale a dente di sega. Questa sottrazione è necessaria per eliminare l'instabilità subarmonica che si manifesta per duty-cycles maggiori del 50%. La trattazione di tale instabilità, che richiede lo studio nel dominio campionato, può essere facilmente trovata online cercando "slope compensation". Dando per assodato che la sua presenza sia necessaria per il corretto funzionamento del convertitore, qui mi occuperò di modellarla nel dominio continuo.
Nello schema è mostrata anche l'accensione del MOSFET di clamp Sc, infatti, come anticipato nella prima parte, questo convertitore attiva in modo complementare S ed Sc: il meccanismo di clamp, che è già stato descritto nella prima parte dell'articolo, non influisce sul meccanismo di regolazione e non sarà più tirato in ballo per ora.
Schematico e blocchi fondamentali
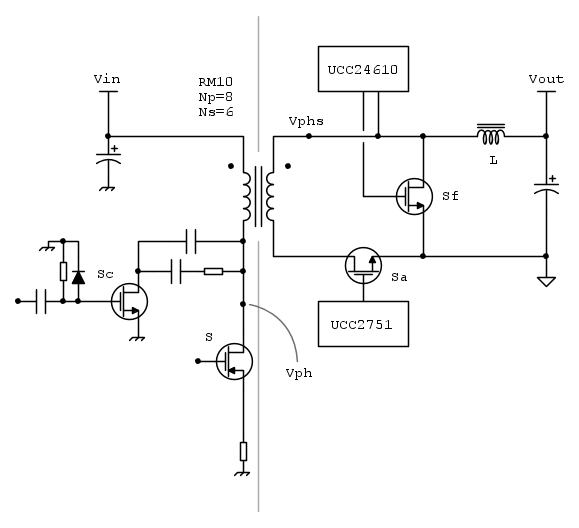
Di seguito lo schematico sempificato del convertitore:
Lo schema completo si può trovare qui. I label nello schema semplificato corrispondono a quelli nello schema completo, in modo da facilitare la lettura di entrambi.
Sezione di potenza
Il convertitore è leggermente diverso rispetto a quanto aticipato: per prima cosa, al secondario non ci sono dei semplici diodi ma si trovato due MOSFET di rettifica con relativi drivers. UCC24610 monitora il drain di Sf implementando un diodo ideale, in pratica accendendo Sf quando la corrente è positiva e spegnendolo quando cambia segno. Questo componente è fondamentale per lasciar entrare il convertitore in modalità DCM, ossia evitando di scaricare l'uscita con correnti di induttore negative a basso carico. Sa è invece pilotato dal primario: idealmente il suo periodo di accensione è lo stesso di S, tuttavia il controller lo accende e spegne con dei ritardi aggiuntivi per motivi di efficienza. Al primario S è ovviamente un NMOS, mentre Sc è un PMOS con una rete di bootstrap. Sia S che Sc sono pilotati da due driver interni al controller, mentre il segnale diretto ad Sa attraversa l'isolamento tramite un optoisolatore, collegandosi poi ad un driver classico.
I dispositivi scelti sono i seguenti:
- S: FDS86140 - MOSFET N-CH, 100 V, 11.2 A, 8SOIC
- Sc: DMP10H400SE - MOSFET P-CH, 100 V, 2.3 A/6 A, SOT223
- Sa: IRFS4310ZTRLPBF - MOSFET N-CH, 100 V, 120 A, D2PAK
- Sf: IRF1018ESTRLPBF - MOSFET N-CH, 60 V, 79 A, D2PAK
- L: SRP1770C-100M - Induttore fisso, 10 μH, 13 mΩ, SMD
I rating in tensione dei MOS sono sovradimensionati, ricordo però che durante la fase di clamp il nodo di phase al primario (il drain di S) deve sopportare la tensione della capacità di clamp, che è maggiore di Vin e dipende dal duty-cycle. La stessa capacità di clamp può crescere in tensione durante i transitori di carico, soprattutto se il controllo ha molta banda, e la tensione n(Vclamp − Vin) viene riflessa al secondario su Sa, quindi in questa versione troverete questo MOS a 100 V che ha ragione di esserci solo perché è una board prototipale. Il linea di massima i rettificatori hanno un margine quasi doppio rispetto al necessario (Sa può essere da 60 V, Sf da 40 V).
È chiaro che scegliendo un rating minore, a parità di area, il dispositivo è meno resistivo e il convertitore più efficiente.
LT3753
Questo controller di Analog Devices gestisce (quasi) tutto il convertitore. Nello schema semplificato è riportato il blocco di regolazione e la logica di driving; tuttavia questo dispositivo si occupa di molte altre cose, tra le quali la gestione di UVLO/OVLO, limitazione del duty-cycle, pulse-skipping, limitazione di corrente, soft-start e alimentazione di servizio. Per maggiori informazioni su tali funzioni rimando allo schema completo e al datasheet del componente.
Viref rappresenta la tensione di picco che può raggiungere lo shunt R12: come introdotto, è una versione scalata della corrente di riferimento ILref che avremmo sull'induttore. La compensazione di rampa viene effettuata con l'iniezione di una corrente a dente di sega Islope sul resistore R14, in pratica sommando alla tensione di shunt una tensione a rampa. Questa tecnica implementa lo stesso comportamento visto in precedenza, solo che la rampa viene sommata ad IL al posto che sottratta ad ILref, quindi il risultato non cambia.
Un clock interno (CLK) setta il latch SR a frequenza fissa: sul MOSFET S si specchia la corrente di L che inizia a crescere linearmente. La corrente (letta sullo shunt e con aggiunta la rampa) viene comparata a Viref. Al raggiungimento del riferimento, il comparatore resetta il latch, esattamente come discusso in precedenza nella sezione Controllo di corrente di picco.
L'uscita del latch è collegata a dei blocchi che ho chiamato DT: questi in realtà rappresentano la logica di tutti i dead times e includono i driver di potenza che alimentano i MOSFET.
Retroazione
Per progettare la rete di controllo è necessario rappresentare il convertitore con un modello di piccolo segnale. Per fare questo, ossia per scrivere delle funzioni di trasferimento nel dominio di Laplace, di può studiare la variazione delle grandezze medie in un periodo di commutazione (in inglese si ottiene un averaged model). Questa tecnica permette di ottenere un modello di piccolo segnale lineare da un convertitore che commuta. Per fare un esempio, nel modello linearizzato la corrente sull'induttore sarà descritta dalla sua media nel periodo Tsw, e l'informazione sul ripple scomparirà.
Prima abbiamo immaginato il convertitore come un generatore di corrente governato dall'errore di tensione: maggiore l'errore, maggiore la corrente (il segno lo vediamo dopo), tuttavia è la funzione di trasferimento in anello aperto che rappresenta la stabilità e le performance che ci interessano (ad esempio margine di fase e di guadagno, banda, guadagno in continua, ecc...). Per tracciarla dobbiamo partire da un punto qualsiasi e percorrere tutto l'anello fino a tornare al punto di partenza, e scoprire di quanto è cambiato il segnale iniziale.
Iniziando dalla tensione di uscita, si può visualizzare l'anello come fosse composto da una rete che legge Vout, lo sottrae al nostro riferimento e genera l'errore di tensione, e dal convertitore che risponde imponendo una corrente sull'induttore. La corrente erogata in uscita incontra l'impedenza di uscita Zout, che manifesta ai suoi capi proprio Vout. Esprimere questo percorso nel dominio di Laplace è tutto ciò che serve per scegliere i valori dei componenti della retroazione.
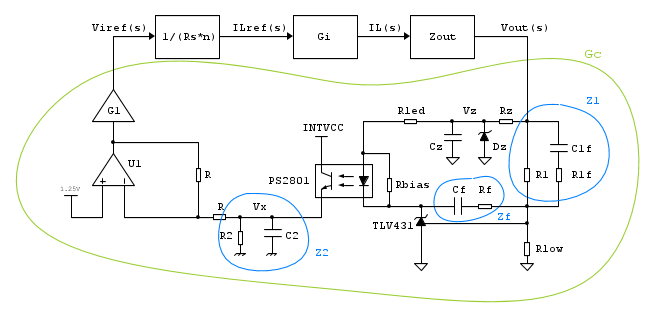
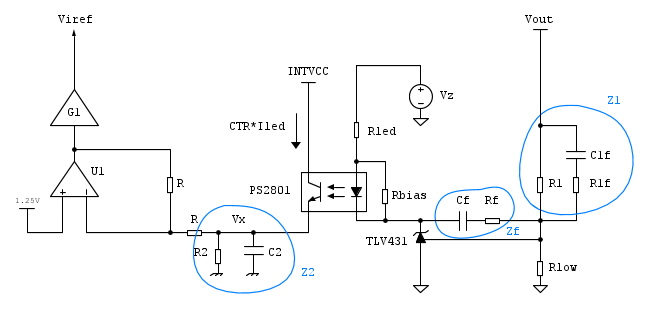
Per lo studio del blocco di retroazione è più semplice osservare lo schema seguente, in cui ho rinominato i componenti in modo più amichevole.
Lo schema in realtà è un po' illegale, non dovrei disegnare componenti passivi e funzioni di trasferimento insieme, ma nel fantastico mondo dell'ingegneria è più comodo fare così. Diciamo che me la sono cavata inglobando tutta la retroazione nell'insieme Gc. Nell'articolo mi riferirò alle grandezze di piccolo segnale con l'iniziale in minuscolo e omettendo la dipendenza da s.
Ho schematizzato il modello linearizzato con quattro funzioni di trasferimento:
Il blocco di retroazione è in pratica rappresentato da Gc(s) (la c starebbe per control), mentre il comportamento del convertitore è descritto dal trasferimento  . L'impedenza di uscita Zout(s) è proprio l'impedenza classica, che nel dominio di Fourier corrisponderebbe al rapporto tra i fasori di tensione e corrente.
. L'impedenza di uscita Zout(s) è proprio l'impedenza classica, che nel dominio di Fourier corrisponderebbe al rapporto tra i fasori di tensione e corrente.
Anello di corrente
Il cuore dell'analisi al piccolo segnale, in questo convertitore, è Gi. Questo guadagno è il rappresentante, al piccolo segnale, di come l'integrato di controllo manovra la corrente di L. Questo induttore, essendo ciccione, segue il riferimento solo quando è abbastanza lento, altrimenti "rimane indietro".
Iniziamo osservando il segnale di riferimento viref: questa tensione rappresenta, come già detto, il picco di corrente che vorrei imporre all'induttore. Per studiare il funzionamento del convertitore abbiamo bisogno della corrente media IL, questo infatti è l'unico modo per lavorare nel dominio di Laplace. La resistenza di shunt, il trasformatore e il funzionamento del latch SR fanno sì che viref si traduca nel vero riferimento di picco IL,iref con un guadagno pari a 1 / (nRs), come mostrato nello schema di prima.
La funzione di trasferimento tra IL,iref ed IL è proprio Gi: essa rappresenta il modo in cui la corrente media su L risponde alle variazioni del riferimento. Per determinare la forma di Gi osserviamo i segnali durante un periodo di commutazione, ossia durante l'intervallo nel quale viene calcolata la media delle grandezze di interesse:
IL,iref può essere scritta come la somma di tre contributi: la corrente media IL (a), metà del ripple di corrente (b) e un pezzo di rampa (c). La rampa, che implementa la compensazione di rampa discussa in precedenza, ha una pendenza di sl A/s. Osservando lo schema circuitale semplificato, questa pendenza è determinata dal generatore di corrente a dente di sega Islope e dalla resistenza R14, che come già discusso può essere immaginato come un dente di sega che si sottrae al riferimento di corrente.
Nel tempo:
 .
.
Il ripple di corrente ΔIL dipende dalla tensione sull'induttore come:
 ,
,
quindi
 .
.
Supponendo che le tensioni "di grande segnale" non cambino, l'equazione linearizzata diventa la seguente:
 ,
,
dove le lettere in minuscolo rappresentano le variazioni delle grandezze corrispondenti. Con l'equazione qui sopra abbiamo ricavato il duty-cycle equivalente che si ottiene nel controllo di corrente di picco con compensazione di rampa. Esplicitando il duty-cycle si ottiene:
 ,
,
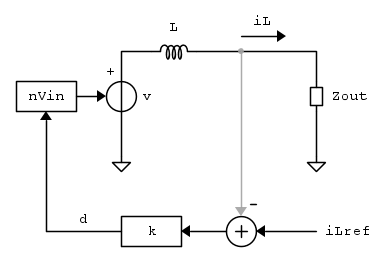
dove k include tutta quella roba scomoda da scrivere. Avendo l'espressione del duty-cycle, si può disegnare lo schema al piccolo segnale seguente:
In pratica, con l'espressione del duty-cycle, possiamo disegnare l'anello di corrente al piccolo segnale: il duty eccita l'induttore con una tensione pari a nVin, mentre la corrente sull'induttore è determinata dal guadagno d'anello e dall'impedenza di uscita. Per conoscere l'espressione in anello chiuso del trasferimento che ci interessa ( ), è prima necessario scrivere l'espressione del guadagno in anello aperto. Per farlo, iniettiamo una corrente di test i' come in figura:
), è prima necessario scrivere l'espressione del guadagno in anello aperto. Per farlo, iniettiamo una corrente di test i' come in figura:
La corrente di test eccita la serie L + Zout con una tensione pari a
 .
.
La corrente su iL è quindi determinata semplicemente come:
 ,
,
ed il guadagno in anello aperto, che chiamiamo Gio, vale:
 .
.
Chiudendo l'anello si ottiene proprio Gi, che come detto corrisponde al trasferimento  . Osservando lo schema per il calcolo dell'anello di corrente, possiamo scrivere
. Osservando lo schema per il calcolo dell'anello di corrente, possiamo scrivere

quindi

che è la classica espressione del sistema retroazionato.
Gio rappresenta la corrente che scorre in un sistema LC-serie (dove C può avere un eventuale carico in parallelo) ad un'eccitazione in tensione, che è in pratica i' moltiplicato per il guadagno  . Di seguito sono riportati i diagrammi di Bode di Gio e Gi con carico in corrente (Zout composta solo dalle capacità di uscita) e con carico resistivo. I diagrammi corrispondono al convertitore in esame, e i parametri sono i seguenti:
. Di seguito sono riportati i diagrammi di Bode di Gio e Gi con carico in corrente (Zout composta solo dalle capacità di uscita) e con carico resistivo. I diagrammi corrispondono al convertitore in esame, e i parametri sono i seguenti:
fsw = 150 kHz
sl = 31μ A\s
Vin = 24 V
Vout = 5 V
L = 13 μH
Cout = 3 mF
n = 0.75
Rload = 500 mΩ (presente solo nel secondo caso)
I due diagrammi sono interessanti perché evidenziano come l'impedenza di uscita influenzi solo la parte a bassa frequenza dell'anello: ad alta frequenza, infatti, si manifesta il polo che dipende dall'induttanza e Zout diventa ininfluente (ammesso che sia di natura capacitiva). In pratica, la banda passante dell'anello dei corrente dipende dall'induttanza, e questo è anche intuitivo: un grosso induttore sarà difficile da "manovrare" ad alta frequenza. In bassa frequenza, invece, la capacità di uscita si fa sentire seguendo la tensione di eccitazione equivalente v, rendendo impossibile l'imposizione di correnti lentamente variabili. Con una resistenza di carico, invece, il guadagno minimo a bassa frequenza viene bloccato ad un valore che dipende da quest'ultima, dove domina rispetto alla parte capacitiva (di fatto a bassissima frequenza è come avere solo la resistenza).
Abbandonando ora le curiosità sull'anello di corrente, si può appurare che la caratteristica fondamentale di questo blocco è proprio la sua banda passante, che dipende principalmente dall'induttore selezionato. La parte a bassa frequenza è di scarso interesse, mentre il polo induttivo andrà ad influenzare pesantemente la banda passante dell'anello di tensione.
Nota: nel caso in esame, l'induttore viene scelto cercando un compromesso tra le sue perdite (nel rame e nel ferro) e il suo volume fisico; in un convertitore più avanzato come potrebbe essere un VRM per carichi digitali, invece, la banda passante è una caratteristica fondamentale del sistema e si cerca il trade-off migliore tra perdite e performance dinamica.
Un'altra nota: come si sceglia la pendenza della slope? In sintesi, esiste un valore di slope che desensibilizza l'anello di corrente dalla tensione di ingresso ed un altro valore (diverso dal primo) che estingue in un solo periodo di commutazione l'oscillazione subarmonica della corrente di induttore. Di solito si sceglie un valore intermedio, (di certo in questa applicazione non è critico), o più comunemente si sceglie quello dell'application note. Altrimenti: a caso e poi si tara in laboratorio.
Il convertitore si comporta quindi come un generatore di corrente controllato: il riferimento iL,ref viene seguito in un range di frequenze che dipende in primo luogo dalla pendenza della slope, dal carico, dalle capacità di uscita e soprattutto dall'induttanza: quest'ultima determina infatti la banda passante dell'anello di corrente.
Da Vi,ref a Vout
Ora che si conosce l'espressione del trasferimento Gi è facile calcolare l'intero "trasferimento" del convertitore: se includiamo, come abbiamo fatto, il carico di uscita all'interno della quantità Zout, possiamo immaginare tutto il sistema di conversione come un'entità che riceve un segnale vi,ref e genera una tensione vout.
Il legame tra vi,ref (ingresso del convertitore) ed iL,ref è semplicemente dato dalla resistenza di sense Rs e dal rapporto di trasformazione, quindi

L'anello di corrente risponde a questo riferimento con il trasferimento Gi analizzato prima, e la corrente di L che ne risulta scorre su Zout, quindi il trasferimento completo vale

Il suo diagramma di Bode è riportato di seguito, nel caso in cui il carico di uscita sia resistivo:
Sensibilità alla variazione dei parametri
Può essere interessante capire come risponda la funzione di trasferimento  alla variazione di alcuni parametri del convertitore. Di seguito sono riportati i diagrammi di Bode nel caso un cui sia modificato il carico, l'induttore di uscita e la tensione di ingresso.
alla variazione di alcuni parametri del convertitore. Di seguito sono riportati i diagrammi di Bode nel caso un cui sia modificato il carico, l'induttore di uscita e la tensione di ingresso.
Dai grafici sopra riportati si possono fare le seguenti considerazioni:
- la resistenza di carico modifica, come introdotto, solo il guadagno "in continua" della FDT di tensione, e non è quindi critico per il dimensionamento del controllo, o meglio non modifica margine di fase, guadagno e banda ottenibile dal sistema. Rimuovendo la resistenza di carico (i.e. con resistenza infinita), la funzione del convertitore presenta un polo nell'origine dato dalla presenza della capacità di uscita in Zout, che "integra" la corrente media di L. Questo si può osservare notando lo spostamento verso le basse frequenze del primo polo all'aumentare della resistenza di carico.
- Il valore di induttanza provoca principalmente una riduzione della banda del convertitore, dato dallo spostamento del polo dell'anello di corrente verso le basse frequenze.
- Il controllo in corrente rende il sistema scarsamente dipendente dalla tensione di alimentazione Vin. Questa è una delle importanti "conquiste" di questa tecnica. La variazione che si osserva nel grafico agisce tramite il guadagno k ricavato nello studio dell'anello di corrente, e dipende inoltre dalla pendenza della slope. La scelta di quest'ultimo parametro dovrebbe garantire il miglior trade-off tra desensibilizzazione da Vin e velocità di smorzamento delle oscillazioni di corrente subarmoniche. L'argomento può essere approfondito online; non inserisco link perché non vorrei che "morissero" dopo qualche tempo.
Per concludere, il controllo deve garantire stabilità e performance nel peggiore dei casi: il controllo in corrente ci viene incontro desensibilizzando il loop dalla tensione di ingresso, che è ampiamente variabile in questo caso. Inoltre, l'induttore non può variare la sua induttanza (se non vicino alla saturazione, cosa che va comunque considerata), mentre le variazioni di carico si manifestano solo in bassa frequenza, scomparendo nella FDT in anello chiuso.
Struttura del regolatore
Analizziamo adesso la funzione di trasferimento GC: essa ha come ingresso la tensione di uscita vout e come uscita la corrente di riferimento (al primario) viref che abbiamo visto prima. Questo blocco si occupa quindi di calcolare l'errore di tensione presente all'uscita, compensarlo e costruire un riferimento di corrente che lo corregga.
Una soluzione comune per chiudere la retroazione in un convertitore isolato è l'utilizzo del TL431/TLV431 (l'ultima è la versione a bassa tensione). Si tratta di un dispositivo a tre terminali con una tensione di riferimento interna che si presta ottimamente al pilotaggio di un optoisolatore.
Come vedremo, questa topologia fornisce due poli (più uno nell'origine e uno dell'optoisolatore) e due zeri per compensare la funzione di trasferimento del convertitore. Sinceramente non sarebbe necessario un controllo così complesso, ma ormai lo uso in modo predefinito. Un'interessante application note di ON Semiconductor sull'uso del TL431 si trova qui, nel quale è anche spiegato come progettare il punto di lavoro in DC.
La retroazione può essere vista come segue: un aumento di Vout provoca una maggiore accensione del TLV, che si manifesta come una maggiore corrente che attraversa il led dell'optoisolatore. La corrente viene specchiata su Z2, provocando quindi un incremento della tensione Vx. Dato che Viref è una versione amplificata e invertita di Vx ed è proprio il riferimento di corrente del convertitore, si verifica una diminuzione di corrente portata in uscita che abbassa Vout.
Supponendo che sia correttamente biased, il TLV431 può essere trattato come un amplificatore operazionale. La funzione di trasferimento da Vout a Viref è molto semplice da calcolare sotto le seguenti ipotesi:
- Vz(s) = 0, ossia variazioni di Vout sono completamente filtrate dallo zener (molto vero).
- La resistenza Rbias non compare nella FDT (abbastanza vero).
-
 : l'impedenza di ingresso dello stadio formato da U1 ed R è molto maggiore di R2, quindi viref = − G1vx. Nota: l'amplificatore invertente interno all'IC trasla vx di 1.25 V: in pratica, questa configurazione permette di lavorare con una tensione nominale di vx = 1.25 V, che rende il biasing della rete di retroazione più semplice.
: l'impedenza di ingresso dello stadio formato da U1 ed R è molto maggiore di R2, quindi viref = − G1vx. Nota: l'amplificatore invertente interno all'IC trasla vx di 1.25 V: in pratica, questa configurazione permette di lavorare con una tensione nominale di vx = 1.25 V, che rende il biasing della rete di retroazione più semplice.
Polarizzazione del regolatore
Prima di impostare la dinamica del regolatore, il TLV e l'optoisolatore devono essere correttamente alimentati. Per trovare il punto di lavoro in DC, si possono fare alcune considerazioni.
- Lo zener Dz serve ad alimentare la rete di retroazione al secondario. Altre configurazioni si collegano direttamente a Vout, ma l'espressione del trasferimento cambia. Con la rete proposta, il segnale è letto solo attraverso Z1. Si sceglie una tensione di zener (minore di Vout) affinché il led dell'optoisolatore e il TLV abbiano sufficiente margine di regolazione. Il cadoto del TLV deve lavorare sopra Vref = 1.24 V, mentre il led ha una tensione di forward di 1.4 V massimi. Il TLV frena la corrente sul led quando Vout aumenta.
- Va considerata la "traduzione" da Vx a IL,ref (c'è di mezzo il guadagno interno G1, un offset di 1.25 V e una traslazione verso l'alto che qui non ho riportato, più il fattore di scala dato da shunt e trasformatore). IL,ref rappresenta la corrente di riferimento sull'induttore, ed i suoi estremi di regolazione dipendono proprio dalla polarizzazione della rete di feedback. Scegliendo opportunamente i suoi estremi (idealmente 0 A e 10 A, ma con un margine aggiuntivo) e scrivendo l'espressione della corrente sul TLV (che dipende da Rled, R2, Vz e CTR), si può creare un sistema di equazioni che definisce il range di valori che coprono il range desiderato. Intuitivamente, quando collego un carico all'uscita, il TLV si interdice tanto da portare il riferimento di corrente sull'induttore al massimo; viceversa, immaginando di scollegare il carico, il TLV assorbe una corrente tale da portare al minimo la corrente in uscita.
- Si può fissare un parametro (ad esempio Rled) e calcolare R2 richiesto per coprire il range di Vx, assicurandosi che il TLV rimanga correttamente polarizzato ai due estremi. Se così non fosse, si può aumentare la tensione di zener, oppure scegliere un optoisolatore con diverso guadagno.
Funzione di trasferimento del regolatore
Dopo aver polarizzato la rete di feedback, si può passare all'analisi dinamica. Come già accennato, il TLV può essere considerato come un amplificatore operazionale: in questo caso, essendoci una tensione di riferimento fissa sull'ingresso non invertente (si veda la figura a inizio paragrafo), al piccolo segnale troviamo 0 V tra Z1 e Zf.
La corrente di piccolo segnale su Z1 è data quindi solo da vout / Z1, ed è la stessa che scorre su Zf: da qui si può ricavare la tensione sul catodo del TLV, e quindi la corrente iled (trascurando la resistenza di bias).
Nota: Rlow scompare dai conti: questa va scelta alla fine dei conti per avere, al centro del partitore, vref alla tensione di uscita desiderata.
Il trasferimento completo vale quindi:


dove CTR è il current transfer ratio dell'optoisolatore e τopto la sua costante di tempo.
Paragonando la FDT così ottenuta con una simulazione circuitale AC otteniamo un'ottima corrispondenza, sintomo che le semplificazioni hanno senso.
A questo punto possiamo progettare il controllo in modo analitico, sicuri che il circuito non nasconde altre non-idealità nella banda di interesse.
Funzione di trasferimento completa in anello aperto
Per ottenere un sistema stabile e robusto si può iterare in un software di calcolo come Matlab la procedura di selezione dei passivi che determinano le performance dinamiche della funzione in anello aperto del sistema completo.
Per prima cosa, vanno selezionati i valori per la polarizzazione del circuito, che sono Vz,Rled,Rbias,R2. In seguito è possibile selezionare le pulsazioni associate a zeri e poli della funzione del controllore, e risolvendo un sistema di equazioni semplici si ottengono i valori R1,R1f,C1f,Rf,Cf,C2. La procedura va iterata fino ad ottenere le prestazioni desiderate: banda, margine di fase e di guadagno.
Rlow si sceglie per ottenere la tensione di uscita desiderata, in funzione della tensione di riferimento interna al TLV. Questo resistore non modifica il loop dinamico.
Con il feedback che ho scelto si ottiene una banda di regolazione di 3.46 kHz, un margine di fase di 107° e un margine di guadagno di 18.8 dB.
PCB
Il convertitore è stato implementato su 2 layers, con rame da 35 μm (1 oz). Tutto il bottom è formato da due ground planes isolati.
Il modulo è stato predisposto per il collegamento ad una scheda industriale, in sostituzione alla precedente soluzione che sfruttava un convertitore monolitico più costoso. Di seguito, oltre al render dei Gerber, due foto del dispositivo montato sulla scheda.
Misure
Il convertitore è stato tarato e testato in laboratorio. Riporterò qui le misure di efficienza, un'analisi termica e le risposte ai transitori.
Efficienza e termiche
Sono state misurate tre curve di efficienza a diverse tensioni di alimentazione:
A basso carico l'efficienza dipende leggermente da Vin, che ha un leggero impatto sulle perdite nel ferro, sul punto di ingresso in modalità CCM e sul convertitore lineare interno al controllore. A medio e alto carico le curve si avvicinano, sintomo che il peso (costante) delle perdite nel ferro diventa poco importante.
Il design del core è stato fatto con una tensione al primario di 16 V, quindi ci si aspetta che le sue performance siano massime in questa situazione. Le immagini termiche a pieno carico, a due tensioni di alimentazioni diverse (Vin = 12 V e Vin = 24 V) e senza ventilazione forzata, mostrano la distribuzione delle perdite nei vari componenti (attenzione che le scale sono diverse, mea culpa).
Confrontando le due immagini del primario, dove viene misurata la temperatura degli avvolgimenti e del MOSFET S, si notano due cose. La prima è che la temperature del core non varia in modo apprezzabile (occhio alla scala): questo è abbastanza sensato in quanto il duty-cycle si stringe all'aumentare della tensione e ΔB rimane circa costante (grazie all'azione del clamp attivo), così come la frequenza che è fissa.
In secondo luogo, le perdite al primario sono maggiori a 12 V: questo comportamento è dovuto alla maggiore corrente media (ed RMS) di primario, che causa l'aumento di temperatura negli avvolgimenti e nel MOSFET.
Al secondario è apprezzabile la ripartizione delle perdite nei due rettificatori sincroni e la temperatura dell'induttore: al variare della tensione di ingresso (e quindi del duty-cycle imposto dal controllore) le perdite a 12 V dominano prima sul rettificatore high-side (in altre parole, il "diodo di ricircolo" si accende per poco tempo), mentre a 24 V l'induttore è per la maggior parte del tempo alimentato dal rettificatore low-side (in altre parole, è quasi sempre in "ricircolo"). L'induttore subisce un leggero aumento del ripple a 24 V, ma l'aumento di temperatura è anche causato dalla connessione fisica al MOSFET di rettifica che è molto caldo.
Le temperature rimangono entro gli 85 °C dopo 30 minuti a pieno carico e senza ventilazione, e in ogni caso nell'applicazione finale questa sarebbe una situazione di sovraccarico temporaneo.
Waveforms in steady-state
Per praticità riporto qui uno schema semplificato.
Di seguito alcune waveforms in vari punti del convertitore.
L'immagine sopra mostra le tensioni di phase al primario e al secondario, rispettivamente Vph e Vphs. Durante l'accensione di S Vph è a 0 V e il secondario viene alimentato attraverso il trasformatore. Durante il tempo di off di S, si nota la scarica del condensatore di clamp sovrapposta a Vin. L'andamento quasi-lineare della scarica è governato da una corrente di magnetizzazione che parte da quasi 0 A: tutta l'energia dell'induttanza di leakage carica il clamp all'inizio di questa fase (sul fronte di spegnimento di S), per caricare la magnetizzante durante tutto il periodo di off, mentre Sa rimane acceso (qui Sa non è mostrato).
Una spiegazione dettagliata del meccanismo di ZVS è riportato nella prima parte dell'articolo, così come un dettaglio di tutti i sotto-intervalli operativi.
Osservando da vicino lo spegnimento di Sa (notare che, essendo un PMOS, il suo spegnimento avviene quando la traccia verde torna a 0 V), si nota il transitorio di quasi-ZVS (Zero Voltage Switching) dell'NMOS S al primario. Riassumendo quanto detto nella prima parte dell'articolo, il segnale di accensione di S (in blu) è attivato quando la sua Vds è prossima agli 0 V: la scarica della capacità del nodo di phase è data dalla corrente nell'induttanza di magnetizzazione del trasformatore, caricata tramite il clamp nella fase "a sinistra", in figura, ed estratta dalla Coss di S durante il dead-time dopo lo spegnimento di Sa. In parole ancora più semplici: la corrente nella magnetizzante del trasformatore assume un valore negativo (è positiva dal clamp verso l'alimentazione) mentre S è spento ed Sa è acceso; allo spegnimento di Sa, tale corrente non può fare altro che "passare" per S: all'inizio questo avviene tramite la capacità del MOS, e poi attraverso il suo diodo intrinseco.
Nella figura sopra il diodo non si accende, in quanto il gate è acceso prima che Vds raggiunga gli 0 V: in laboratorio questo tempo può essere tarato e dipende da vari fattori quali la tensione di alimentazione nominale, il carico nominale e il gap del trasformatore. In questa topologia, tra l'altro, il transitorio di ZVS è fortemente dipendente da carico, in quanto l'energia della leakage è predominante nella carica del clamp. Aumentando il gap del trasformatore la magnetizzante si riduce, il transitorio di scarica lineare del clamp si trasforma in un arco di sinusoide e il dead-time può essere ridotto, ma come effetto negativo si ha l'incremento delle perdite di conduzione a basso carico. Per questo range di tensione le perdite di switching non hanno molta importanza, inoltre in questa applicazione il regime di basso carico occupa la maggior parte del tempo: per questo il gap del core è minimo, la magnetizzante ha un valore elevato e lo ZVS è incompleto; d'altro canto, le perdite a basso carico sono molto più basse che negli altri test a gap maggiore.
(Ho scambiato le sonde e i colori si sono invertiti, abbiate pazienza). Le due immagini sopra mostrano il funzionamento in CCM e DCM con due carichi diversi. Il funzionamento in DCM, in particolare, è garantito dall'integrato di rettifica UCC24610, che implementa in pratica un diodo ideale.
Questo è invece il ripple della tensione di uscita a pieno carico, che non supera i 50 mV.
Transitori di carico
Il carico da alimentare tramite questo convertitore è di natura principalmente digitale, ma ci sono anche alcune batterie di elettromagneti che potrebbero dare qualche "botta" di tanto in tanto. Lo studio della funzione di trasferimento non è propriamente sufficiente e capire come si comporta il convertitore quando i carichi variano, dato che molte parti del dispositivo potrebbero saturare o non essere più lineari. In più, esistono diverse modalità di funzionamento che non sono rappresentate dallo schema a blocchi linearizzato dei capitoli precedenti. Per essere certi della robustezza del modulo, questo deve essere ampiamente testato tramite un carico attivo e in tutto il range di funzionamento.
Non solo il convertitore deve mantenere la stabilità "classica", ma deve anche evitare di "incastrarsi" in stati di protezione come overcurrent (hiccup mode nel datasheet) o eccessiva limitazione di duty-cycle (volt-second limiter nel datasheet). Durante i transitori, inoltre, il rating di tensione sui semiconduttori deve rimanere entro limiti di sicurezza, specialmente in questa topologia dove entra in gioco una dinamica di "grande segnale" data dal clamp. In fase transitoria, infatti, i MOSFET S ed Sa devono sopportare una sovratensione che può essere di molto superiore alla Vds di regime. Questi fattori vanno (prima simulati e poi) valutati in laboratorio, eventualmente agendo sulle impostazioni del controllore.
Un esempio: con una banda maggiore di quella qui riportata, il controllo innescava la protezione di sovracorrente. Dato che una limitazione di corrente che non inneschi la protezione non esiste in questo integrato, l'unica soluzione è stata quella di diminuire la banda del controllo. Con una banda "consona", invece, la dinamica rimane quella di un sistema quasi lineare e la protezione non scatta. Anche se fosse stata disponibile una limitazione di corrente di picco, la dinamica studiata con Laplace non sarebbe stata valida durante l'azione del limitatore.
Dato che il convertitore opera in due (tre) modalità di funzionamento (pulse-skipping + DCM/CCM), è stato anche valutato il passaggio da una all'altra. La modalità pulse-skipping, molto comune in questo tipo di conversioni, si innesca per bassi carichi: quando l'uscita non eroga corrente, infatti, il segnale che rappresenta la corrente di picco scende sotto una soglia interna che ne determina l'innesco. Il controller in questo caso spegne tutti i segnali di driving, lasciando che l'uscita si scarichi lentamente. Quando il feedback riporta il comp sopra la soglia (con una certa isteresi), viene generato un treno di commutazioni che ripristina Vout. Il processo si ripete fino a che il carico non aumenta, e durante questo tempo il consumo di energia è estremamente ridotto. D'altro canto, questa modalità corrisponde a qualcosa di fortemente non-lineare e si comporta in modo isteretico.
Nell'immagine sopra è mostrata l'evoluzione della tensione di uscita ad un transitorio di carico nella modalità CCM, ossia nel modo di funzionamento studiato in questo articolo. Il controllo assicura Vout un ripple simmetrico (siamo chiaramente in una zona lineare) di +/- 150 mV.
Nel caso sopra, invece, il convertitore commuta tra le modalità pulse-skipping e quella CCM, rispettivamente con 0 A (nessun carico) e 10 A (carico massimo). In questo caso si osserva un "buco" di -600 mV e un picco di +150 mV. Il buco è -diciamo- lungo da studiare, ma non esisterebbe in modalità CCM forzata. Chiaramente, forzando tale modalità, ci sarebbero perdite elevatissime a basso carico e non è assolutamente necessario in questa particolare applicazione.
Il transitorio tra modalità è di seguito "zoommato", inserendo anche la tensione di phase al primario.
La tensione di phase, che ci indica la modalità operativa del convertitore, mostra come nella modalità di pulse-skipping il convertitore smetta effettivamente di commutare per risparmiare energia (di driving, di conduzione, associata alle perdite nel ferro, ecc..). Dato che il controllo è stato progettato per la modalità CCM, queste fasi di assestamento non sono una sorpresa; proprio per questo è necessaria una fase di controllo in laboratorio.
Appendice: il soft-start
L'ultimo tassello che vorrei citare (tutti i tasselli sono necessari, ma pochi sono interessanti) è la gestione del soft-start. Tale soft-start è necessario sempre, in qualsiasi convertitore di tensione con delle capacità di uscita. Riassumendo, le capacità di uscita all'inizio dei tempi sono scariche: queste devono passare -quando arriva l'alimentazione all'ingresso- da 0 V a Vout,ref, 5 V nel nostro caso. Dato che un passaggio a "gradino" richiede, per definizione, una potenza infinita, il passaggio deve essere graduale.
Se questo non dovesse bastare, si potrebbe anche tirare in ballo la banda infinita che servirebbe per avere un transitorio di Vout estremamente veloce. Inoltre, per chiudere (e spero sia sufficiente), potremmo anche pensare di fornire una tensione di riferimento "a gradino", ma rischieremmo di trovarci a fine transitorio con l'integratore della rete di feedback completamente saturo (wind-up) e con un'oscillazione marcata della tensione di uscita (se non è un'oscillazione è almeno un overshot). Insomma, l'uscita deve passare dolcemente da zero a ciò che vogliamo, e questo tipicamente si fa tramite una Vout,ref che cresce a rampa fino al valore di regime.
L'integrato di controllo fornisce tale sistema, ossia una tensione di riferimento che, usciti dall'UVLO, cresce a rampa. Tuttavia, per come è fatta la rete di feedback, questo meccanismo non ci è utile.
Osserviamo la rete di feedback nello schematico finale:
Immaginando uno schema senza i componenti nel rettangolo arancione, supponiamo che il convertitore (a riposo) riceva l'alimentazione e che l'integrato di controllo generi al suo interno una rampa di riferimento (cosa che è veramente così).
La tensione di uscita vale 0 V, e la rete di feeback non è alimentata. L'optoisolatore non è illuminato, e la tensione Vx (pin 3 di U2) vale circa 0 V: da subito, il picco di corrente di riferimento generato dal regolatore cresce rapidamente insieme alla tensione di riferimento interna. L'uscita inizia a caricarsi, e con un certo ritardo il feedback viene alimentato tramite R26 e D3.
In sintesi, la rampa dell'ingresso termina ancora prima che la rete di feedback si svegli: in questa parte dell'esistenza del convertitore c'è una gara tra la rampa, l'accensione del TLV e la carica sul condensatore C14. Può darsi che il feedback venga agganciato in tempo, ma la cosa è difficile da prevedere.
Per questo motivo sono stati inseriti i componenti nel rettangolo arancione: all'accensione, C23 è scarico e permette l'alimentazione della base di Q5. Appena l'uscita raggiunge una tensione sufficiente ad accendere l'optoisolatore, il suo catodo viene "scaricato" attraverso Q5. La rampa di riferimento al primario è quindi inutile, e determina solo l'evoluzione dei primi istanti di commutazione. Per costruzione, appena Vout inizia a crescere, il feedback frena la crescita della corrente di riferimento al primario.
Dopo un po' di tempo, C23 inizia ad essere sazio di carica, e Q5 inizia a spegnersi: in questa fase, il feedback inizia a partizionare la corrente verso il TLV, che prende il controllo della corrente dell'optoisolatore. Durante questo processo la tensione di uscita non cresce linearmente, ma almeno lo fa senza discontinuità (e questo è l'importante).
Da qui in poi, il feedback regola l'uscita, e allo spegnimento le tensioni sono ripristinate a quelle di "boot" (C23 si scarica con la sua mesh di resistori). Lo startup l'ho registrato con un oscilloscopio più triste, ma si vede bene comunque:
Vbase è la tensione di base di Q5.
Conclusioni
Non c'è molto da concludere, il convertitore funziona come previsto ed è anche carino da vedere.
Al momento lo sto utilizzando come dimostratore nel laboratorio dell'Università degli studi di Udine, specialmente quando i ragazzi delle superiori vengono in visita (ho appena finito il PhD e ora sto facendo un assegno di ricerca). Ho notato che sono molto attratti dalle immagini termiche: mi piace programmare il carico per commutare periodicamente facendo "respirare" la scheda inquadrata sullo schermo.
Questo è anche uno dei convertitori più semplici per concretizzare varie nozioni nel corso di Elettronica di Potenza, soprattutto per mostrare -a scheda accesa- come cambino le waveforms all'oscilloscopio (ad esempio facendo leva sulla ferrite per aumentare il gap, osservando la scarica del phase che arriva a "toccare terra" accendendo il diodo del MOS al primario, ed osservando la corrente in ingresso che si modifica), oppure misurando il guadagno d'anello iniettando segnali di test.
In più, sono contento che sia servito per abbattere il costo della conversione dell'energia in un'applicazione industriale.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)