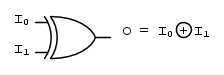Elettrotecnica e non solo (admin)
Un gatto tra gli elettroni (IsidoroKZ)
Esperienza e simulazioni (g.schgor)
Moleskine di un idraulico (RenzoDF)
Il Blog di ElectroYou (webmaster)
Idee microcontrollate (TardoFreak)
PICcoli grandi PICMicro (Paolino)
Il blog elettrico di carloc (carloc)
DirtEYblooog (dirtydeeds)
Di tutto... un po' (jordan20)
AK47 (lillo)
Esperienze elettroniche (marco438)
Telecomunicazioni musicali (clavicordo)
Automazione ed Elettronica (gustavo)
Direttive per la sicurezza (ErnestoCappelletti)
EYnfo dall'Alaska (mir)
Apriamo il quadro! (attilio)
H7-25 (asdf)
Passione Elettrica (massimob)
Elettroni a spasso (guidob)
Bloguerra (guerra)
Prima di vedere come si possono ridurre le funzioni logiche ricavate come indicato nel precedente articolo LogicBignami (IV), con quello che adesso conosciamo delle tabelle della verità, possiamo concludere quello che avevamo lasciato in sospeso ossia l'analisi della funzione logica EX-OR e delle porte logiche EX-OR e EX-NOR.
Indice |
La porta logica EX-OR
Nell'articolo LogicBignami (II), abbiamo visto che la tabella della verità della funzione logica EX-OR è la seguente:
| fA(x) | fB(x) |  |
|---|---|---|
| 0 | 0 | 0
|
| 0 | 1 | 1
|
| 1 | 0 | 1
|
| 1 | 1 | 0
|
Possiamo così ricavare la funzione 
, che avevamo preannunciato nel summenzionato articolo, dall'analisi dei mintermini corrispondenti allo stato logico 1 della funzione stessa:
 |
La porta logica, che realizza la funzione EX-OR, avrà lo stesso simbolo grafico, la stessa tabella della verità e funzione logica in cui, al posto delle funzione booleane, in ingresso, avremo le variabili d'ingresso 
:
e 
:
| I1 | I0 |  |
|---|---|---|
| 0 | 0 | 0
|
| 0 | 1 | 1
|
| 1 | 0 | 1
|
| 1 | 1 | 0
|
Analizzando sempre i mintermini corrispondenti allo stato logico 1 della variabile d'uscita 
otteniamo:
 |
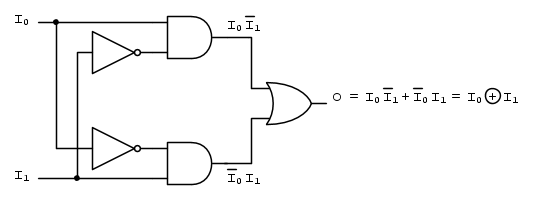
Questa funzione logica ci permette di ricavarne il circuito digitale interno: come si vede si tratta di una somma logica (che viene svolta da una porta logica OR) di due prodotti logici (che verranno svolti da due porte logiche AND).
Quindi la porta logica EX-OR equivale ad una porta logica OR ai cui ingressi sono collegate due porte logiche AND ai cui rispettivi ingressi giungono le variabili e alternativamente complementate:
Ricordando la schematizzazione per mezzo di generici interruttori elettronici delle porte logiche AND, OR e NOT, viste nell'articolo LogicBignami (III), si ottiene questo circuito:
Nel rispetto della tabella della verità si nota che solo quando gli ingressi e presentano stati logici opposti, cioè uno connesso alla tensione 
(condizione logica "VERO" - 1 logico) e l'altro connesso a 
(condizione logica "FALSO" - 0 logico), è possibile che l'uscita venga collegata alla tensione di alimentazione (condizione logica "VERO" - 1 logico) tramite la coppia di interruttori 
o 
, in caso contrario l'uscita si troverà a 0V, cioè in una condizione di "FALSO" (0 logico).
La porta logica EX-OR con sole porte NAND
Partendo dalla realizzazione in logica AOI della porta EX-OR vista in precedenza e ricordando come possono essere realizzate le porte logiche AND, OR e NOT con le sole porte logiche NAND (vedi sempre l'articolo LogicBignami (III)), si ottiene il seguente schema:
In pratica, in alto, è rappresentata la mera sostituzione di ogni singola porta logica con la corrispondente realizzazione mediante porte logiche NAND: si è evidenziato, nei singoli rettangoli tratteggiati, la porta logica corrispondente emulata.
Dall'analisi di questo primo schema si nota la presenza di due porte logiche NAND, configurate come porte logiche NOT collegate in serie (evidenziate dall'asterisco rosso).
Ricordando la proprietà della doppia negazione queste possono essere eliminate e, di conseguenza, si ottiene lo schema definitivo della porta logica EX-OR con sole porte logiche NAND.
In quest'ultimo schema, applicando alla funzione logica relativa all'uscita , prima la Legge di De Morgnan e, successivamente, la già citata proprietà della doppia negazione si ottiene, com'è giusto che sia, la funzione logica EX-OR.
La porta logica EX-OR con sole porte NOR
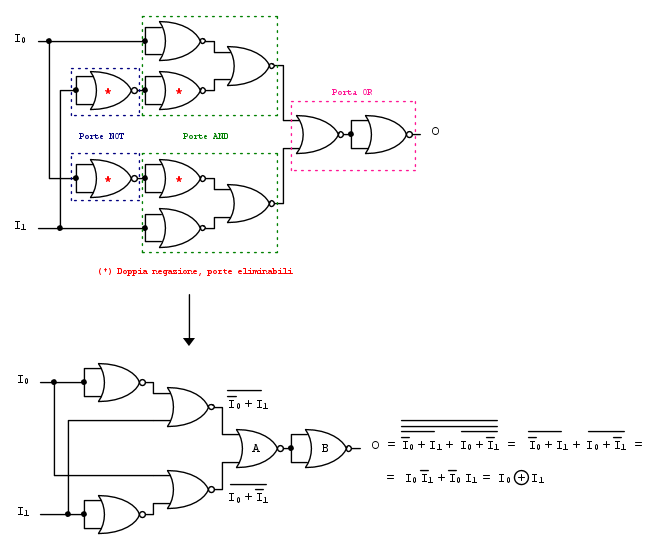
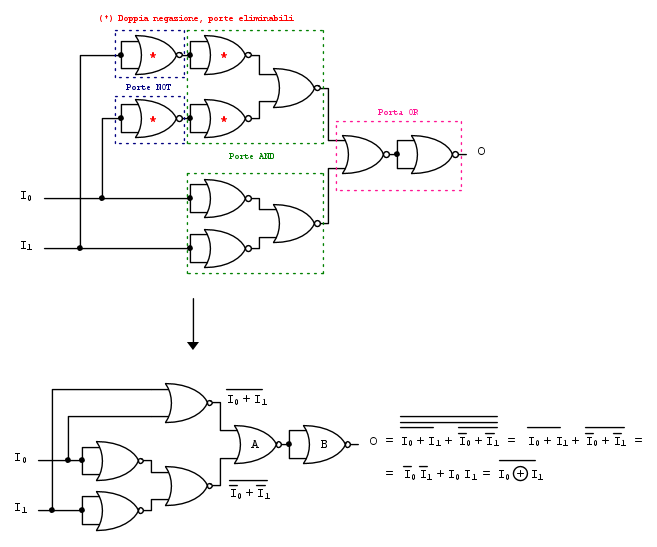
Anche in questo caso partiamo dalla realizzazione in logica AOI della porta EX-OR e ricordando come possono essere realizzate le porte logiche AND, OR e NOT con le sole porte logiche NOR vediamo come se ne realizza lo schema:
Nell'immagina, in alto, è rappresentata la mera sostituzione di ogni singola porta logica con la corrispondente realizzazione mediante porte logiche NOR, evidenziando, nei singoli rettangoli tratteggiati, la porta logica corrispondente emulata.
Dall'analisi di questo primo schema si nota, anche in questo frangente, la presenza di due porte logiche NOR, configurate come porte logiche NOT collegate in serie (evidenziate dall'asterisco rosso), per cui, ricordando la propietà della doppia negazione queste possono essere eliminate e, di conseguenza, si può ottenere lo schema definitivo della porta logica EX-OR con sole porte logiche NOR.
In quest'ultimo schema, applicando alla funzione logica relativa all'uscita , prima la propietà della doppia negazione (*) e successivamente, alle due somme logiche complementate, la Legge di De Morgan, si ottiene la funzione logica EX-OR.
(*) Nota: I due segni di complementazione totali sono dovuti, uno, alla negazione della porta logica NOR (A) e, l'altro, alla porta logica NOR (B) in configurazione NOT.
La porta logica EX-NOR
Questa porta logica equivale al complemento (negazione) della funzione logica EX-OR, cioè una porta logica EX-OR alla cui uscita è collegata una porta logica NOT, e viene rappresentata con il seguente simbolo grafico:
In pratica, la porta logica EX-NOR ha lo stesso simbolo della porta logica EX-OR con evidenziato, all'uscita, un cerchio che rappresenta la negazione effettuata sulla somma logica (in pratica sottintende la presenza della porta logica NOT connessa all'uscita).
Di conseguenza, questa porta logica risponde alla seguente tabella della verità:
| I1 | I0 |  |
|---|---|---|
| 0 | 0 | 1
|
| 0 | 1 | 0
|
| 1 | 0 | 0
|
| 1 | 1 | 1
|
Per ricavare la funzione logica relativa all'uscita prendiamo in esame i mintermini corrispondenti allo stato logico 1 dell'uscita stessa, ottenendo:
 |
In realtà, essendo, per definizione, il complemento della funzione logica EX-OR, si potrebbe anche ricavare applicando la Legge di De Morgan alla funzione logica di partenza:
ma per la complementarietà (vedi l'articolo LogicBignami (II)), i termini 
e 
equivalgono ad uno stato logico 0, e rappresentano, quindi, elementi neutri per la somma logica.
Quind, semplificando, si ottiene la formula finale della funzione logica EX-NOR:
come dall'analisi dei mintermini fatta poco sopra.
Anche in questo caso, la funzione logica ci permette di ricavarne il circuito digitale interno: come per la prota logica EX-OR abbiamo una somma logica (che viene svolta da una porta logica OR) di due prodotti logici (che vengono svolti da due porte logiche AND).
Pertanto la porta logica EX-NOR equivale ad una porta logica OR ai cui ingressi sono collegate due porte logiche AND: ad una di queste giungeranno le variabili d'ingresso e normali, mentre all'altra giungeranno complementate:
Da questo si può ricavare il circuito schematizzato con generici interruttori elettronici:
Come si può notare, nel rispetto della tabella della verità, solo quando gli ingressi e presentano stati logici identici, cioè entrambi connessi alla tensione (condizione logica "VERO" - 1 logico) oppure entrambi connessi a (condizione logica "FALSO" - 0 logico), è possibile che l'uscita venga collegata alla tensione di alimentazione (condizione logica "VERO" - 1 logico) tramite la coppia di interruttori (chiusi se entrambi gli ingressi sono in condizione logica "VERO") o (chiusi se entrambi gli ingressi sono in condizione logica "FALSO").
Viceversa l'uscita si troverà a 0V, cioè in una condizione di "FALSO" (0 logico) in quanto uno interruttore, in ognuna delle due coppie citate, risulterà aperto.
Quanto era stato detto per le porte logiche NAND e NOR, nell'articolo LogicBignami (III), in merito alla semplice aggiunta di una porta logica NOT al circuito corrispondente alla funzione logica non complementata, vale anche per la porta logica EX-NOR: si può fare ma il circuito che ne risulterebbe conterrebbe un interruttore elettronico in più dello stretto necessario.
La porta logica EX-NOR con sole porte NAND e sole porte NOR
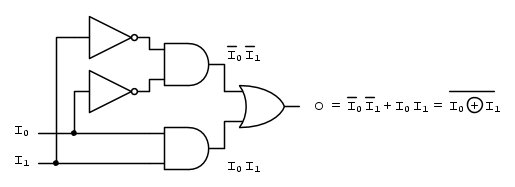
Il procedimento per realizzare una porta logica EX-NOR con sole porte logiche NAND, o con sole porte logiche NOR, è identico a quello poch'anzi illustrato per la porta logica EX-OR, quindi mi limito a riportare i due circuiti equivalenti.
EX-NOR con sole NAND
EX-NOR con sole NOR
E con questa parentesi abbiamo concluso con la descrizione delle porte logiche, dal prossimo articolo riprenderemo con i procedimenti da utilizzare per ridurre, quando è possibile, le funzioni booleane che si ricavano dall'esame delle tabelle della verità.