Indice |
Premessa
Durante la preparazione dell'esame di costruzioni elettromeccaniche ho ricevuto preziosi aiuti dagli autorevoli membri del forum e, tra questi, RenzoDF, parlando di flussi dispersi nei trasformatori (vedi discussione), ha posto una questione interessante che mi ha stimolato a scrivere questo articolo.
Nel calcolo "manuale", che chiamerò classico, delle induttanze di dispersione, occorrono delle assunzioni spesso anche abbastanza forti per poter affrontare questo tipo di studio in modo sufficientemente semplificato. Questo articolo si propone di indicare brevemente quali sono le approssimazioni e le ipotesi fatte , quali sono i risultati e, soprattutto, di fare un confronto con i risultati ottenuti tramite simulazione agli elementi finiti del medesimo problema, per poter valutare l'entità dell'eventuale discostamento dai risultati prettamente teorici.
In questo articolo mi limiterò a considerare il caso di un trasformatore monofase con avvolgimento concentrico semplice cioè un avvolgimento formato da due "tubi" concentrici.
Calcolo teorico: assunzioni e metodo di calcolo
Per calcolare il valore di induttanza di dispersione Ldisp utilizzeremo il calcolo dell'energia magnetica e quindi useremo le seguenti due formule essenziali:
Dove H ed B sono rispettivamente campo e induzione magnetica e V è il volume di integrazione, ovvero il volume in cui esistono le linee di campo generate dagli avvolgimenti.
La definizione di questo volume è alla base del calcolo classico.
L'ipotesi principale utilizzata nello studio classico delle macchine elettriche è senz'altro quello di considerare infinito il valore di permeabilità magnetica μr. Questo significa che le linee di flusso avranno come via preferenziale di richiusura il nucleo del trasformatore: possiamo assumere nullo il valore di riluttanza magnetica  di quest'ultimo e possiamo trascurare la corrente di magnetizzazione e assumere quindi N1I1 = N2I2 = NI (dove con N intendiamo il numero di spire di un avvolgimento e con I la corrente che li percorre).
di quest'ultimo e possiamo trascurare la corrente di magnetizzazione e assumere quindi N1I1 = N2I2 = NI (dove con N intendiamo il numero di spire di un avvolgimento e con I la corrente che li percorre).
A questo punto vediamo come scegliere il volume di integrazione. Per capire meglio utilizzerò uno schema che rappresenta una induttanza avvolta in aria nella quale scorre una corrente Idc.
Le linee tratteggiate in verde rappresentano in modo schematico l'andamento delle linee di flusso generate dalla corrente Idc che percorre il solenoide.
Possiamo quindi valutare due regioni:
- Regione interna al solenoide
- All'interno del tubo del solenoide possiamo considerare uniforme la distribuzione di linee di flusso e quindi considerare costante il campo magnetico H.
- Regione esterna al solenoide
- Possiamo intuire dal disegno come, all'esterno del tubo, le linee di flusso tendano ad allargarsi e, pertanto, l'induzione B tende ad essere nulla e, poiché in aria vale la relazione B = μ0H, possiamo ritenere nullo il valore di campo.
Ai fini del nostro calcolo questo vuol dire assumere che tutta l'energia magnetica sia compresa all'interno dei cilindri formati dagli avvolgimenti ovvero nel tubo compreso tra il diametro interno del primo avvolgimento e il diametro esterno del secondo.
Risultati del calcolo classico
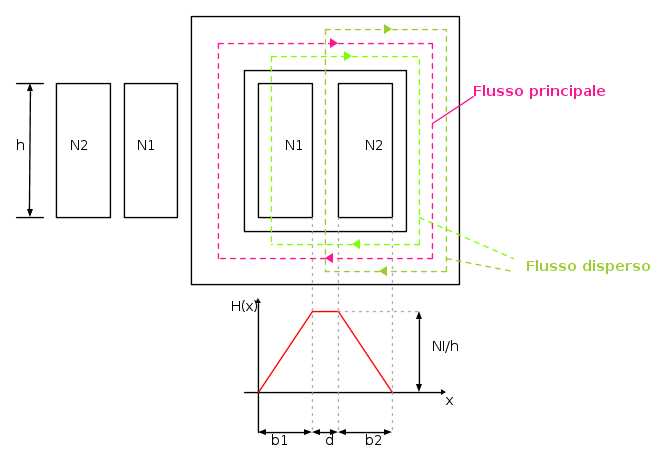
Una volta effettuate le opportune semplificazioni ed ipotesi presentate nel precedente paragrafo, è possibile fornire un risultato analitico. Considerando la figura seguente avremo:

e quindi

Occorre fare qui altre due piccole precisazioni.
- L'uso del termine Rm, che rappresenta il raggio medio dei due avvolgimenti, è un'ulteriore approssimazione di tipo geometrico che si basa sul fatto che gli avvolgimenti sono principalmente sviluppati in altezza (h > > Rm > b). Questo termine ingloba in se tutti i raggi medi relativi ai due avvolgimenti e all'interspazio d fra i due.
- L'aver considerato l'altezza del volume di integrazione pari all'altezza dell'avvolgimento comporta il trascurare tutta l'energia magnetica nel tratto compreso tra l'avvolgimento e il giogo. D'altra parte, usare l'altezza delle colonne del nucleo, avrebbe voluto dire considerare uniforme il campo in una regione in cui questo non lo è. La soluzione migliore potrebbe essere considerare un'altezza h media fra l'altezza dell'avvolgimento e la distanza fra i gioghi.
- L'incremento lineare del campo all'aumentare della distanza dalla colonna presuppone una distribuzione uniforme della densità di corrente nella sezione dell'avvolgimento. Ipotesi piuttosto forte visto che il trasformatore, per definizione, lavora in corrente alternata: questo comporta la presenza di effetto pelle e correnti parassite che modificano la distribuzione della densità di corrente.
Per poter avere dei valori numerici da confrontare poi con i risultati che deriveranno dalla simulazione, useremo i seguenti valori delle grandezze di interesse:
 (N=1 per la simulazione)
(N=1 per la simulazione)
ottenendo un valore dell'energia magnetica  e quindi un valore dell'induttanza di dispersione
e quindi un valore dell'induttanza di dispersione  .
.
Simulazione
Per la simulazione utilizzerò il software FEMM (Finite Element Method Magnetics): un software di simulazione agli elementi finiti per problemi elettromagnetici totalmente freeware. FEMM è un programma in 2D quindi, a sua volta, introdurrà comunque un errore dovuto alla valutazione planare di un problema spaziale, ma il grado di approssimazione introdotto è sicuramente di molto inferiore rispetto al calcolo effettuato precedentemente!
Occorre, come primo passo, produrre un disegno della geometria e assegnare i relativi materiali e le condizioni al contorno.
Una volta eseguite le operazioni preliminari, si "mesha" la regione da simulare, ovvero si divide lo spazio complessivo in tante piccole aree per discretizzare il problema. Femm, come quasi tutti i programmi per la simulazione di campi elettromagnetici, usa elementi triangolari a 3 nodi.
A questo punto possiamo lanciare la simulazione!
La prima cosa che il programma permette di visualizzare è l'andamento delle linee di campo.
Con gli strumenti messi a disposizione dal software è possibile effettuare il confronto con i risultati del calcolo classico.
Come prima cosa vediamo che, l'andamento del campo magnetico non si discosta effettivamente molto dal trapezio (almeno per la parte interna alla "finestra" del nucleo):
Salta subito all'occhio il fatto che, nella regione tra i due avvolgimenti, il campo non è costante.
Sfruttando gli strumenti di calcolo, possiamo ora calcolare l'energia magnetica. (Nota: le linee di flusso che percorro l'intero nucleo concatenando i due avvolgimenti, contribuiscono al flusso principale e concatenano una forza magneto-motrice complessivamente nulla: non danno contributi all'integrale. Difatti, grazie alle ipotesi fatte, queste linee non vengono considerate nel calcolo classico. Con la simulazione fem non occorre più tale distinzione).
Come si può leggere dal riquadro nell'immagine, si ottiene una energia magnetica  dalla quale si ricava una induttanza di dispersione
dalla quale si ricava una induttanza di dispersione  .
.
Conclusioni
Per concludere facciamo un breve riepilogo comparativo dei risultati ottenuti:
| Induttanza di dispersione μH | Energia magnetica J | |
|---|---|---|
| Calcolo classico | 0.40 | 
|
| Simulazione fem | 0.34 | 
|
Questo significa che, rispetto alla simulazione agli elementi finiti (in 2D), il modello utilizzato per il calcolo classico conduce a risultati discosti di un valore inferiore al 20%.
L'analisi porta a ritenere valido il modello classico per una valutazione preliminare dell'induttanza di dispersione e, comunque, ne giustifica totalmente l'uso didattico! (Capisco che l'idea di tanti belli (?) integrali non entusiasmi particolarmente noi studenti, ma, almeno, il sapere che hanno un senso pratico può aiutare a digerirli ;) )
Limitazioni del presente lavoro e possibili ulteriori sviluppi
Nello scrivere il presente articolo ho concentrato l'attenzione su un particolare tipo di avvolgimento, il concentrico semplice. La disposizione con un semi avvolgimento all'esterno, pur non essendo una geometria tipicamente usata nella pratica, è stata utilizzata per permettere di visualizzare meglio la geometria del problema.
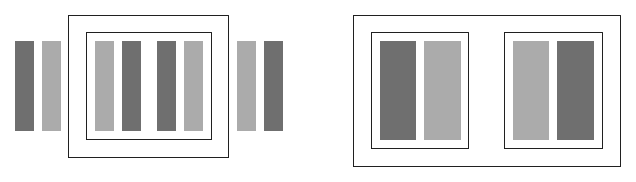
Le disposizioni tipicamente usate sono quelle che schematizzo nel disegno seguente.
Inoltre, pur potendo escludere conclusioni di molto diverse da quelle ottenute per questo tipo di avvolgimento, restano da esplorare gli altri due principali tipi di avvolgimenti ovvero l'avvolgimento concentrico doppio e l'avvolgimento alternato (detto anche a disco o a tamburo).
Bibliografia
- Appunti del corso di Costruzioni Elettromeccaniche, Prof. M. Pastorelli, corso di Laurea Specialistica in Ingegneria Elettrica Politecnico di Torino;
- Metodologia di progettazione delle macchine elettriche, N. Bianchi, S. Bolognai, CLEUP, 2011
- http://www.femm.info/wiki/InductanceExample
- http://www.electroyou.it/admin/wiki/femmtutorial

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)